Eulersche Betafunktion
Die Eulersche Betafunktion, auch Eulersches Integral 1. Art
(nach Leonhard
Euler) ist eine mathematische
Funktion zweier komplexer
Zahlen, die mit
bezeichnet wird. Ihre Definition lautet:
wobei
und
einen positiven Realteil
haben müssen.
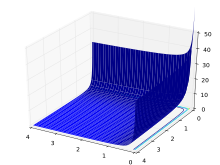
Die Betafunktion tritt unter anderem bei der Betaverteilung auf.
Allgemeines
Bei festem
(bzw.
)
ist
eine meromorphe
Funktion von
(bzw.
),
und für die Funktion gilt die Symmetrierelation
.
Es existieren folgende weitere Integraldarstellungen für die Betafunktion mit
und
(die erste Darstellung ergibt sich durch die Substitution
)
An der Darstellung mit der Gammafunktion kann man ablesen, dass die
analytische Fortsetzung der Betafunktion Pole
genau entlang
und
für ganze
Zahlen
hat.
Theodor
Schneider zeigte 1940, dass die Zahl
für alle rationalen, nicht ganzzahligen
transzendent
ist.
Beziehung zur Gammafunktion
Das Hauptresultat der Theorie der Betafunktion ist die Identität
wobei
die Eulersche Gammafunktion
bezeichnet.
Um diese Relation herzuleiten, kann man das Produkt der Gammafunktionen schreiben als:
nun kann man die Variablen
und
substituieren und erhält damit
Teilt man nun beide Seiten durch ,
erhält man das Resultat.
Darstellungen
Die Betafunktion hat viele weitere Darstellungen wie:
Die Betafunktion kann, durch Anpassen der Indizes, zur Definition der Binomialkoeffizienten verwendet werden:
Mit der Darstellung für die Gammafunktion kommt man für ganzzahlige positive
und
auf:
.
Ableitung
Die Ableitung ist gegeben durch
wobei
die Digamma-Funktion
ist.
Werte
Aus der Eulerschen Formel des Ergänzungssatzes ergibt sich folgende Formel:
Viele Beta-Funktionswerte für rationale Zahlenpaare sind mit der Kreiszahl und mit vollständigen elliptischen Integralen erster Art darstellbar.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.02. 2022