Orthogonale Matrix
 |
 | |
|
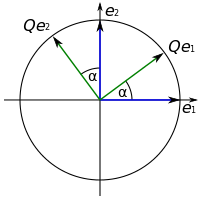
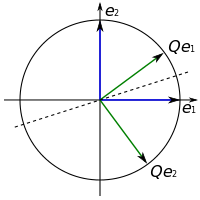
Durch Multiplikation mit einer orthogonalen
Matrix Q können Vektoren gedreht (links) oder gespiegelt (rechts)
werden. Die Länge der Vektoren und der Winkel zwischen den Vektoren
bleiben dabei erhalten. | ||
Eine orthogonale Matrix ist in der linearen Algebra eine quadratische, reelle Matrix, deren Zeilen- und Spaltenvektoren orthonormal bezüglich des Standardskalarprodukts sind. Damit ist die Inverse einer orthogonalen Matrix gleichzeitig ihre Transponierte.
Orthogonale Matrizen stellen Kongruenzabbildungen im euklidischen Raum, also Drehungen, Spiegelungen und Kombinationen daraus, dar. Jede orthogonale Abbildung zwischen zwei endlichdimensionalen Skalarprodukträumen kann nach Wahl je einer Orthonormalbasis durch eine orthogonale Matrix dargestellt werden. Die Menge der orthogonalen Matrizen fester Größe bildet mit der Matrizenmultiplikation als Verknüpfung die orthogonale Gruppe.
Orthogonale Matrizen werden beispielsweise bei der numerischen Lösung linearer Gleichungssysteme oder Eigenwertprobleme eingesetzt. Der analoge Begriff bei komplexen Matrizen ist die unitäre Matrix.
Definition
Eine reelle quadratische
Matrix
heißt orthogonal, wenn das Produkt
mit ihrer transponierten
Matrix
die Einheitsmatrix
ergibt, also
gilt. Werden die Spaltenvektoren
der Matrix
mit
bezeichnet, dann ist diese Bedingung gleichbedeutend damit, dass das Standardskalarprodukt
zweier Spaltenvektoren
ergibt, wobei
das Kronecker-Delta
ist. Die Spaltenvektoren einer orthogonalen Matrix bilden damit eine Orthonormalbasis des
Koordinatenraums
.
Dies trifft auch für die Zeilenvektoren einer orthogonalen Matrix zu, denn mit
ist auch
orthogonal, das heißt
.
Auch wenn die Bezeichnung „orthogonale Matrix“ so verstanden werden könnte, reicht es nicht aus, wenn die Zeilen- oder Spaltenvektoren lediglich paarweise orthogonal sind; sie müssen zusätzlich normiert sein, also die Länge eins aufweisen.
Beispiele
Konkrete Beispiele
- Die Matrix
- ist orthogonal, denn es gilt
-
.
- Auch die Matrix
- ist orthogonal, denn es gilt
-
.
Allgemeine Beispiele
- Permutationsmatrizen,
also Matrizen, bei denen genau ein Eintrag pro Zeile und Spalte gleich eins
ist und alle anderen Einträge null sind, sind orthogonal. Bezeichnet
die zu einer Permutation
zugehörige Permutationsmatrix, dann gilt
-
,
- denn die transponierte Permutationsmatrix ist gleich der Permutationsmatrix der inversen Permutation, die alle Vertauschungen rückgängig macht, und das Produkt von Permutationsmatrizen entspricht der Hintereinanderausführung der Permutationen. Die vorzeichenbehafteten Permutationsmatrizen, bei denen in jeder Zeile und Spalte genau ein Eintrag plus oder minus eins ist und alle übrigen Einträge null sind, sind genau die ganzzahligen orthogonalen Matrizen.
- Drehmatrizen, also Matrizen, die eine Drehung um den Koordinatenursprung in der euklidischen Ebene beschreiben, sind orthogonal. Bezeichnet
- die Drehmatrix einer Drehung um einen Winkel
, die den Ursprung festlässt, dann gilt mit dem „trigonometrischen Pythagoras“
-
.
- Allgemeiner sind auch Drehmatrizen, die eine Drehung in einer beliebigen
Ursprungsebene im
-dimensionalen Raum beschreiben, orthogonal.
- Spiegelungsmatrizen, also Matrizen, die eine (senkrechte) Spiegelung an einer Ursprungsgerade in der euklidischen Ebene beschreiben, sind orthogonal. Bezeichnet
- die Spiegelungsmatrix einer Spiegelung an einer Ursprungsgerade mit
Einheits-Normalenvektor
, dann gilt
-
,
- denn Spiegelungsmatrizen sind nach Definition symmetrisch und
für einen Einheitsvektor
gilt
. Allgemeiner sind auch Matrizen, die Spiegelungen an einem beliebigen Untervektorraum im
-dimensionalen Raum (beispielsweise einer Hyperebene) beschreiben, orthogonal.
Eigenschaften
Inverse
Eine orthogonale Matrix
ist aufgrund der linearen
Unabhängigkeit ihrer Zeilen- und Spaltenvektoren stets regulär. Die Inverse einer
orthogonalen Matrix ist dabei gleich ihrer Transponierten, das heißt, es gilt
.
Die Inverse einer Matrix
ist nämlich gerade diejenige Matrix
,
für die
gilt. Aus der zweiten Gleichung folgt weiterhin, dass die Transponierte einer
orthogonalen Matrix orthogonal ist. Es gilt auch die Umkehrung und jede Matrix
,
deren Transponierte gleich ihrer Inversen ist, ist orthogonal, denn es gilt dann
.
Längen- und Winkeltreue
Wird ein Vektor
mit einer orthogonalen Matrix
multipliziert, ändert sich die Länge (euklidische
Norm) des Vektors nicht, das heißt
.
Weiter ist das Standardskalarprodukt zweier Vektoren
invariant bezüglich der Multiplikation mit einer orthogonalen Matrix
,
also
.
Damit bleibt auch der Winkel zwischen den beiden Vektoren erhalten. Beide Eigenschaften folgen direkt aus der Verschiebungseigenschaft des Standardskalarprodukts. Aufgrund dieser Längen- und Winkeltreue stellt die lineare Abbildung
eine Kongruenzabbildung im euklidischen Raum dar. Umgekehrt ist die Abbildungsmatrix bezüglich der Standardbasis jeder winkeltreuen linearen Abbildung im euklidischen Raum orthogonal. Aufgrund der Polarisationsformel ist auch jede längentreue Abbildung winkeltreu.
Determinante
Für den Betrag
der Determinante einer
orthogonalen Matrix
gilt
,
was mit Hilfe des Determinantenproduktsatzes über
folgt. Damit kann die Determinante einer orthogonalen Matrix nur die Werte eins oder minus eins annehmen. Es gibt allerdings auch nicht-orthogonale Matrizen, deren Determinante plus oder minus eins ist, zum Beispiel unimodulare Matrizen. Orthogonale Matrizen, deren Determinante eins ist, entsprechen Drehungen. Man spricht dann auch von einer eigentlich orthogonalen Matrix. Orthogonale Matrizen, deren Determinante minus eins ist, stellen Drehspiegelungen dar. Man spricht dann auch von einer uneigentlich orthogonalen Matrix.
Eigenwerte
Die Eigenwerte
einer orthogonalen Matrix
sind nicht notwendigerweise alle reell. Sie haben jedoch den komplexen
Betrag eins, sind also von der Form
mit .
Ist nämlich
ein zu
gehöriger Eigenvektor, dann gilt aufgrund der Längentreue und der absoluten
Homogenität einer Norm
und daher .
Eine orthogonale Matrix besitzt demnach höchstens die reellen Eigenwerte
.
Die komplexen Eigenwerte treten immer paarweise komplex konjugiert
auf, das heißt mit
ist auch
ein Eigenwert, denn
.
Demnach besitzt eine orthogonale Matrix ungerader Dimension
mindestens einen reellen Eigenwert (siehe auch den Satz vom
Fußball).
Diagonalisierbarkeit
Eine orthogonale Matrix
ist normal,
das heißt, es gilt
,
und damit über den komplexen
Zahlen unitär diagonalisierbar.
Nach dem Spektralsatz
gibt es nämlich eine unitäre
Matrix ,
sodass
gilt, wobei
eine Diagonalmatrix mit den Eigenwerten von
ist. Die Spaltenvektoren von
sind dann paarweise orthonormale Eigenvektoren von
.
Damit sind auch die Eigenräume
einer orthogonalen Matrix paarweise orthogonal.
Im Allgemeinen ist eine orthogonale Matrix
jedoch nicht reell diagonalisierbar. Es existiert allerdings eine orthogonale
Matrix
,
sodass
eine Blockdiagonalmatrix
ergibt, bei der die einzelnen Blöcke entweder Drehmatrizen der Größe
sind oder aus der Zahl
oder
bestehen. Diese Darstellung wird auch Normalform einer orthogonalen Matrix
genannt.
Normen
Die Spektralnorm einer
orthogonalen Matrix
ist
.
Für die Frobeniusnorm gilt mit dem Frobenius-Skalarprodukt entsprechend
.
Das Produkt mit einer orthogonalen Matrix erhält sowohl die Spektralnorm, als
auch die Frobeniusnorm einer gegebenen Matrix ,
denn es gilt
und
.
Damit bleibt auch die Kondition einer Matrix bezüglich dieser Normen nach Multiplikation mit einer orthogonalen Matrix erhalten.
Orthogonale Matrizen als Gruppe
Die Menge der regulären Matrizen fester Größe bildet mit der
Matrizenmultiplikation als Verknüpfung
eine Gruppe,
die allgemeine
lineare Gruppe .
Als neutrales
Element dient dabei die Einheitsmatrix
.
Die orthogonalen Matrizen bilden eine Untergruppe
der allgemeinen linearen Gruppe, die orthogonale
Gruppe
.
Das Produkt zweier orthogonaler Matrizen
ist nämlich wieder orthogonal, denn es gilt
.
Weiter ist die Inverse einer orthogonalen Matrix
ebenfalls orthogonal, denn es gilt
.
Die orthogonalen Matrizen mit Determinante eins, also die Drehmatrizen,
bilden wiederum eine Untergruppe der orthogonalen Gruppe, die Drehgruppe (oder spezielle
orthogonale Gruppe) .
Dabei handelt es sich um eine Lie-Gruppe,
d.h. die Gruppenoperationen sind verträglich mit dem Differenzieren in der
Gruppe, und Elemente von
lassen sich als Exponentiale von Matrizen aus der zugehörigen Lie-Algebra darstellen. Die
orthogonalen Matrizen mit Determinante minus eins, also die Drehspiegelungen,
bilden keine Untergruppe der orthogonalen Gruppe, sondern lediglich eine Nebenklasse,
denn ihnen fehlt das neutrale Element.
Verwendung
Lineare Gleichungssysteme
Die Lösung linearer Gleichungssysteme der Form
mit einer orthogonalen Matrix
und einer rechten Seite
lässt sich numerisch
effizient durch
berechnen. Die Ermittlung der Lösung
erfordert also lediglich eine Matrix-Vektor-Multiplikation,
die mit einem Aufwand der Ordnung
durchgeführt werden kann. Im Vergleich dazu benötigt die Lösung allgemeiner
linearer Gleichungssysteme beispielsweise mit Hilfe der Gauß-Elimination
einen Aufwand
.
Dieser Vorteil wird beispielsweise bei der (reellen) diskreten
Fourier-Transformation und der diskreten
Kosinus-Transformation genutzt.
Matrixzerlegungen
Eine weitere Anwendung orthogonaler Matrizen ist die QR-Zerlegung einer
gegebenen Matrix
als Produkt
einer orthogonalen Matrix
und einer oberen Dreiecksmatrix
.
Die Konstruktion der Matrix
kann dabei mit Givens-Rotationen,
die Drehungen entsprechen, oder Householdertransformationen,
die Spiegelungen entsprechen, durchgeführt werden. QR-Zerlegungen werden in der
Numerik bei der Lösung schlecht konditionierter, überbestimmter oder
unterbestimmter linearer Gleichungssysteme eingesetzt. Ein weiteres
Anwendungsfeld besteht in der Berechnung von Eigenwertproblemen mit dem QR-Algorithmus.
Mit Hilfe der Singulärwertzerlegung
lässt sich jede reelle Matrix
auch als Produkt
einer orthogonalen Matrix ,
einer Diagonalmatrix
und der Transponierten einer weiteren orthogonalen Matrix
darstellen. Die Diagonaleinträge der Matrix
sind dann die Singulärwerte von
.
Die Singulärwertzerlegung wird beispielsweise in der Geometrie
bei der Hauptachsentransformation
von Quadriken und in der Statistik bei der
Hauptkomponentenanalyse
multivariater Datensätze eingesetzt.
Eine quadratische Matrix
kann mittels der Polarzerlegung
auch als Produkt
einer orthogonalen Matrix
und einer positiv
semidefiniten symmetrischen Matrix
faktorisiert werden.
Orthogonale Abbildungen
Ist
ein
-dimensionaler
reeller Skalarproduktraum,
dann lässt sich jede lineare
Abbildung
nach Wahl einer Orthonormalbasis
für
durch die Abbildungsmatrix
darstellen, wobei
für
ist. Die Abbildungsmatrix
ist nun genau dann orthogonal, wenn
eine orthogonale
Abbildung ist. Dies folgt aus
,
wobei
und
sind.
Siehe auch
Literatur
- Jörg Liesen, Volker Mehrmann: Lineare Algebra. Springer, 2011, ISBN 978-3-8348-8290-5.
- Hans Rudolf Schwarz, Norbert Köckler: Numerische Mathematik. Springer, 2009, ISBN 978-3-8348-0683-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.02. 2021