Drehspiegelung

Wird der Punkt P zunächst um die schwarze Drehachse gedreht und dann an der blauen Ebene gespiegelt (oder umgekehrt), so erfolgt die Projektion auf den Punkt Q. Wird er hingegen nach der Drehung am Inversionszentrum (roter Punkt in der blauen Ebene) gespiegelt (oder umgekehrt), so erfolgt die Projektion auf den Punkt Q'.

Eine Drehspiegelung ist eine Kongruenzabbildung des dreidimensionalen euklidischen Raumes in sich. Sie ist zusammengesetzt aus einer Drehung und einer Spiegelung an einer Ebene, die von der Drehachse rechtwinklig geschnitten wird. Eine verwandte Abbildung ist die Drehinversion, die aus einer Drehung und einer Spiegelung an einem Punkt der Drehachse besteht. In beiden Fällen spielt die Reihenfolge der Teiloperationen Drehung und Spiegelung bei der Ausführung keine Rolle. Drehspiegelung und Drehinversion liefern dasselbe Ergebnis, wenn (i) das Inversionszentrum der Schnittpunkt der Spiegelebene mit der Drehachse ist und (ii) sich die beiden Drehwinkel um $\pi =180^{\circ }$ unterscheiden. Beide Abbildungen sind Bewegungen des euklidischen Raums, die wegen der Spiegelungen die Orientierung umkehren.

Die Drehwinkel 0° und 180° liefern besonders einfache Ergebnisse:

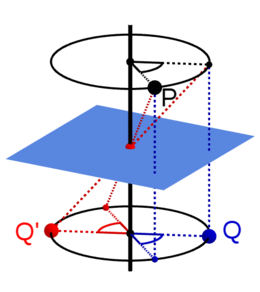
Eine Drehspiegelung um 0° (= Drehinversion um 180°) ist eine einfache Ebenenspiegelung: Der Punkt P der nebenstehenden Abbildung wird entlang der blauen Linie senkrecht nach unten projiziert.
Eine Drehspiegelung um 180° (= Drehinversion um 0°) ist eine Punktspiegelung am Schnittpunkt der Spiegelebene mit der Drehachse (in der Abbildung der rote Punkt in der blauen Ebene): Der Punkt P wird also entlang der roten Linie schräg nach hinten und unten projiziert.

Da es sich tatsächlich um eine Punktspiegelung handelt, hängt das Ergebnis in diesem Fall nicht von der Lage der Achse ab, solange diese durch das Inversionszentrum geht.

Wird der Ursprung eines kartesischen Koordinatensystems in das Inversionszentrum gelegt, so wird eine Drehspiegelung durch eine orthogonale Matrix mit Determinante –1 dargestellt. Wenn außerdem die -Achse als Drehachse gewählt wird, nimmt die Form

$A={\begin{pmatrix}\cos \varphi &-\sin \varphi &0\\\sin \varphi &\cos \varphi &0\\0&0&-1\end{pmatrix}}$

an. Bei einer Drehinversion hat die Matrix dieselbe Form, es muss lediglich $\varphi$ durch $\varphi +\pi$ ersetzt werden.

Die wiederholte Anwendung einer Drehspiegelung mit dem Winkel $\varphi$ liefert abwechselnd Drehspiegelungen und gewöhnliche Drehungen. Die zugehörigen Winkel sind $\varphi$ , $2\varphi$ , $3\varphi$ , … Ist $\varphi ={\tfrac {2\pi }{n}}$ , so ist auch eine Drehung um ein Vielfaches von $2\pi$ dabei, so dass insgesamt nur endlich viele verschiedene Abbildungen auftreten. Diese bilden eine Gruppe, die zur Beschreibung von Kristallstrukturen und Molekülsymmetrieen verwendete Drehspiegelgruppe.

Literatur

Martin Nitschke: Geometrie. Anwendungsbezogene Grundlagen und Beispiele. Carl-Hanser-Verlag, 2005, ISBN 3-446-22676-1.

Basierend auf einem Artikel in:

Wikipedia.de