Satz von Bolzano-Weierstraß

Der Satz von Bolzano-Weierstraß (nach Bernard Bolzano und Karl Weierstraß) ist ein Satz der Analysis.

Formulierungen des Satzes von Bolzano-Weierstraß

Für den Satz von Bolzano-Weierstraß gibt es folgende Formulierungen, die alle äquivalent zueinander sind:

Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) enthält (mindestens) eine konvergente Teilfolge.
Jede beschränkte Folge komplexer Zahlen (mit unendlich vielen Gliedern) hat (mindestens) einen Häufungspunkt.
Jede beschränkte Folge reeller Zahlen hat einen größten und einen kleinsten Häufungspunkt.

Beweisskizze

Der Beweis der allgemeinen Aussagen wird auf die eindimensionale reelle Aussage zurückgeführt. Diese kann man beweisen, indem man gleichzeitig eine Intervallschachtelung $(I_{k}=[u_{k},v_{k}])_{{k\in \mathbb{N} }}$ und eine Teilfolge $(a_{{n_{k}}})_{{k\in \mathbb{N} }}$ konstruiert, so dass für jedes $k\in\N$ gilt $a_{{n_{k}}}\in I_{k}$ . Diese zwei Folgen werden rekursiv konstruiert.

Als Startpunkt dient das Intervall $I_{1}=[u_{1},v_{1}]=[-L,\,L]$ , wobei L eine Schranke der Folge ist, d.h. alle Folgeglieder sind im Intervall enthalten. Weiter kann $a_{{n_{1}}}=a_{1}$ als erstes Glied der zu bestimmenden Teilfolge gesetzt werden.
Im Schritt von k zu k+1 enthält das Intervall unendlich viele Folgeglieder.
1. Zuerst wird das Intervall $I_{k}=[u_{k},v_{k}]$ halbiert in $[u_{k},t_{k}]$ und $[t_{k},v_{k}]$ mit dem Mittelpunkt $t_{k}={\tfrac 12}(u_{k}+v_{k})$ .
2. Es können nicht in beiden Teilintervallen nur endlich viele Folgeglieder liegen. Es kann also immer ein Teilintervall mit unendlich vielen Folgenglieder ausgewählt werden, diese Hälfte wird mit $I_{{k+1}}$ bezeichnet.
3. Schließlich wird das nächste Glied $a_{{n_{{k+1}}}}$ der Teilfolge als das erste Element bestimmt, das in $I_{{k+1}}$ liegt und dessen Index größer ist als der des zuvor gewählten Elements, $m>n_{k}$ .
Der Rekursionsschritt wird für alle $k\in\N$ durchgeführt. Das betrachtete Intervall wird dabei immer kleiner, $|I_{{k+1}}|={\tfrac 12}|I_{k}|$ , die Länge konvergiert gegen Null, wie es von einer Intervallschachtelung verlangt wird. Nach der Konstruktion ist der gemeinsame Punkt aller Intervalle $\textstyle \bigcap _{{k\in \mathbb{N} }}I_{k}=\{x^{*}\}$ , auch schon der Grenzwert der Teilfolge, $\textstyle \lim _{{k\to \infty }}a_{{n_{k}}}=x^{*}$ , und damit ein Häufungspunkt der vorgegebenen beschränkten Folge.

Um den größten Häufungspunkt zu bestimmen, muss man, wann immer möglich, das obere Teilintervall wählen, für den kleinsten Häufungspunkt das untere Teilintervall.

Der Beweis beruht entscheidend auf dem Intervallschachtelungsprinzip, welches wiederum äquivalent ist zur Vollständigkeit der reellen Zahlen.

Visualisierung der Beweisskizze

Gegeben sei eine beschränkte Folge $(x_{n})_{n\in \mathbb {N} }$ . Diese besitzt damit eine untere Schranke und eine obere Schranke .
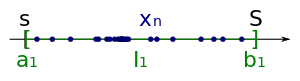Als erstes Intervall der Intervallschachtelung wählt man $I_{1}=[s,S]$ .
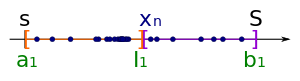Das Intervall $I_{1}$ wird in zwei gleich große Teilintervalle unterteilt.
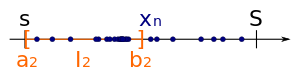Als zweites Intervall $I_{2}$ der Intervallschachtelung wählt man das Teilintervall, welches unendlich viele Folgenglieder von $(x_{n})_{n\in \mathbb {N} }$ besitzt. Wenn beide Teilintervalle unendlich viele Glieder von $(x_{n})_{n\in \mathbb {N} }$ besitzen, wählt man irgendeines der beiden Teilintervalle als $I_{2}$ .
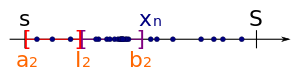Das Intervall $I_{2}$ wird wieder in zwei Teilintervalle zerlegt.
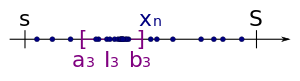Auch hier wählt man das Teilintervall als drittes Intervall $I_{3}$ , welches unendlich viele Folgeglieder von $(x_{n})_{n\in \mathbb {N} }$ besitzt.
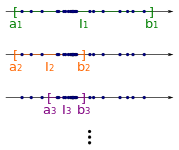Diesen Prozess wiederholt man unendlich oft. So erhält man eine Intervallschachtelung $(I_{n})_{n\in \mathbb {N} }$ . Aus dem Intervallschachtelungsprinzip folgt, dass es eine Zahl gibt, die in allen Intervallen enthalten ist. Diese Zahl ist dann auch Häufungspunkt der Folge $(x_{n})_{n\in \mathbb {N} }$ .

Verallgemeinerungen

Endlichdimensionale Vektorräume

Die komplexen Zahlen werden im Kontext dieses Satzes als zweidimensionaler reeller Vektorraum betrachtet. Für eine Folge $(a_{n})_{{n\in \mathbb{N} }}\subset \mathbb{R} ^{n}$ von Spaltenvektoren mit n reellen Komponenten wählt man zuerst eine Teilfolge, die in der ersten Komponente konvergiert. Von dieser wählt man wieder eine Teilfolge, die auch in der zweiten Komponente konvergiert. Die Konvergenz in der ersten Komponente bleibt erhalten, da Teilfolgen konvergenter Folgen wieder konvergent mit demselben Grenzwert sind. Und so weiter, bis die n-te Teilfolge auch in der letzten Komponente konvergiert.

Unendlichdimensionale Vektorräume

Der Satz von Bolzano-Weierstraß gilt nicht in unendlichdimensionalen normierten Vektorräumen. So ist z.B. die Folge der Einheitsvektoren (0,0,...,0,1,0,...,0,...) im Folgenraum $\ell _{2}(\mathbb{R} )$ beschränkt, hat aber keinen Häufungspunkt, da alle Folgenglieder einen Abstand von ${\sqrt {2}}$ voneinander haben. Dieses Gegenbeispiel lässt sich auf beliebige unendlichdimensionale normierte Räume verallgemeinern, man kann darin immer eine unendliche Folge von Vektoren der Länge 1 konstruieren, die untereinander paarweise einen Abstand von wenigstens 1/2 besitzen.

Als Ersatz für den Satz von Bolzano-Weierstraß in unendlichdimensionalen Vektorräumen existiert in reflexiven Räumen folgende Aussage: Jede beschränkte Folge eines reflexiven Raumes besitzt eine schwach konvergente Teilfolge. Zusammen mit den sobolevschen Einbettungssätzen liefert die Existenz von schwach konvergenten Teilfolgen beschränkter Folgen häufig Lösungen von Variationsproblemen und damit partiellen Differentialgleichungen.

Folgerungen und Verallgemeinerungen

Aus dem Satz von Bolzano-Weierstraß folgt, dass jede monotone und beschränkte Folge reeller Zahlen konvergiert (Monotoniekriterium) und dass eine stetige Funktion auf einem abgeschlossenen und beschränkten Intervall ein Maximum bzw. ein Minimum annimmt (Satz vom Minimum und Maximum).

Der Satz von Bolzano-Weierstraß ist eng verwandt mit dem Satz von Heine-Borel. Eine Verallgemeinerung beider Sätze auf topologische Räume ist folgender: Ein topologischer Raum ist genau dann ein kompakter Raum, wenn jedes Netz ein konvergentes Teilnetz hat.

Basierend auf einem Artikel in:

Wikipedia.de