
Intervallschachtelung
Das Intervallschachtelungsprinzip wird besonders in der Analysis in Beweisen benutzt und bildet in der numerischen Mathematik die Grundlage für einige Lösungsverfahren.
Das Prinzip ist Folgendes: Man fängt mit einem beschränkten Intervall an und wählt aus diesem Intervall ein abgeschlossenes Intervall, das komplett in dem vorherigen Intervall liegt, wählt dort wieder ein abgeschlossenes Intervall heraus und so weiter. Werden die Längen der Intervalle beliebig klein, konvergiert also ihre Länge gegen Null, so gibt es genau eine reelle Zahl, die in allen Intervallen enthalten ist. Wegen dieser Eigenschaft können Intervallschachtelungen herangezogen werden, um mit ihnen die reellen Zahlen als Zahlbereichserweiterung der rationalen Zahlen zu konstruieren.
Grundideen in Form des Arguments der vollständigen Teilung finden sich bereits bei Zenon von Elea und Aristoteles.
Definition
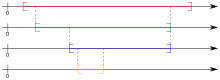
Seien
rationale oder reelle Zahlenfolgen,
monoton wachsend und
monoton fallend,
für alle
,
und bilden die Differenzen
eine Nullfolge, also
,
dann wird die Folge
oder auch
der Intervalle
als Intervallschachtelung bezeichnet.
Konstruktion der reellen Zahlen
Es gilt nun, dass es für jede Intervallschachtelung rationaler Zahlen
höchstens eine rationale Zahl
gibt, die in allen Intervallen enthalten ist, die also
für alle
erfüllt.
Es stimmt aber nicht, dass jede Intervallschachtelung rationaler Zahlen
mindestens eine rationale Zahl
enthält; um eine solche Eigenschaft zu erhalten, muss man die Menge
der rationalen Zahlen zur Menge
der reellen Zahlen erweitern.
Dies lässt sich beispielsweise mit Hilfe der Intervallschachtelungen
durchführen. Dazu sagt man, jede Intervallschachtelung definiere eine
wohlbestimmte reelle Zahl, also
.
Da Intervalle Mengen sind, kann zur Verdeutlichung des Schnitts aller
Intervalle der Schachtelung auch geschrieben werden:
.
Die Gleichheit reeller Zahlen definiert man dann über die entsprechenden
Intervallschachtelungen:
genau dann, wenn stets
und
.
Auf analoge Weise lassen sich die Verknüpfungen reeller Zahlen als Verknüpfungen von Intervallschachtelungen definieren; beispielsweise ist die Summe zweier reeller Zahlen als
definiert.
Dieses so definierte System hat nun die gewünschten Eigenschaften, insbesondere gilt nun, dass jede beliebige Intervallschachtelung rationaler Zahlen genau eine reelle Zahl enthält.
Intervallschachtelungen sind aber nicht die einzige Möglichkeit zur Konstruktion der reellen Zahlen; insbesondere ist die Konstruktion als Äquivalenzklasse von Cauchy-Folgen weiter verbreitet. Weiterhin gibt es noch die Methode der Dedekindschen Schnitte.
Konvergenz der Grenzfolgen einer Intervallschachtelung
Sei
eine Intervallschachtelung, die die Zahl
definiert. Dann ist
Beweis: Sei ein beliebiges reelles
vorgegeben. Zum Nachweis der Konvergenz
der Grenzfolgen
ist zu zeigen, dass nach Wahl eines geeignetes
für alle
beide Intervallgrenzen
in einer
-Umgebung
von
liegen.
Da
eine Intervallschachtelung und daher
,
eine Nullfolge ist, existiert ein
so, dass
für alle
.
Bildlich: Für alle
ist der Durchmesser der Intervalle der Schachtelung so klein, dass keine der
Intervallgrenzen
mehr eine Grenze der
-Umgebung
von
erreicht, wenn das betrachtete Intervall
enthalten soll.
Rechnung: Mit
ist
.
Für
ist mit
:
, wegen
ist insgesamt
;
, wegen
ist insgesamt
, q.e.d.
Weitere Anwendungen
- Der Zwischenwertsatz von Bolzano lässt sich mit dem Intervallschachtelungsprinzip beweisen.
- Die Bisektion ist ein numerisches Verfahren, das auf der Intervallschachtelung basiert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.11. 2019