
Substitutionsmischkristall
Als Substitutionsmischkristall oder Austauschmischkristall wird ein Mischkristall bezeichnet, bei dem mindestens zwei Stoffe einen gemeinsamen Kristall bilden und die Atome der zweiten Komponente (die Fremdatome) auf regulären Gitterplätzen der ersten Komponente sitzen, sie ersetzen also an bestimmten Stellen die Atome der ersten Komponente.
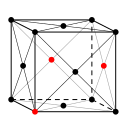  |
| schwarz = Atome des Elementes 'A' rot = Atome des Elementes 'B' |
Notwendige Voraussetzungen sind:
- annähernd gleich große Atome (Differenz max. 15 %)
- gleiche Gitterkonfiguration (die Kristallart A und B muss dieselbe sein)
- chemische Affinität der Komponenten (etwa gleiche Anzahl an Valenzelektronen; Metalle müssen im Periodensystem benachbart, Elektronegativitäten ähnlich sein)
Häufig sind die Fremdatome im Kristall vollkommen regellos (also statistisch) verteilt. Ein Substitutionsmischkristall mit statistischer Anordnung stellt keine stöchiometrische Verbindung der einzelnen Komponenten dar.
Für die Gitterkonstante des Mischkristalls gilt näherungsweise die Vegardsche Regel, nach der sich diese aus dem arithmetischen Mittel der Gitterkonstanten der Komponenten ergibt.
Sonderfälle
Spezialfälle der Substitionsmischkristalle sind:
- Überstrukturen (oder Fernordnung), die bei bestimmten stöchiometrischen Mischungsverhältnissen der Komponenten auftreten (Beispiel: CuAu, Cu3Au). Hierbei liegen die Fremdatome in einer geordneten Verteilung / regelmäßigen Anordnung vor.
- Nahordnung, bei der die Wirtsatome größere, zusammenhängende Bereiche bilden, die Fremdatome dagegen seltener direkt nebeneinander liegen bzw. keine völlig regellose Anordnung haben.
- einphasige oder kohärente Entmischung (Clusterbildung): die gelösten Fremdatome liegen in bestimmten Bereichen, den Zonen, in größerer Konzentration vor (Anreicherung); dies hat besondere Bedeutung bei ausscheidungsgehärteten Werkstoffen (z.B.: AlCuMg, AlMgSi).
Beispiele
- Legierungen:
- Cu-Ni
- Cu-Au
- Ag-Au
- Aluminium-Lithium-Legierungen
Literatur
- Charles Kittel: Einführung in die Festkörperphysik. Oldenbourg, 11. Auflage 1996, ISBN 3-486-23596-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.01. 2024