Gleichdruckprozess

Gleichdruckprozess im p-V-Diagramm: charakteristisch exponentieller Druckanstieg 1➝2 durch starke isentrope Kompression bis zum oberen Totpunkt, gefolgt von einem Abschnitt mit isobarer Expansion 2➝3 während der Wärmezufuhr, danach exponentieller Abfall 3➝4 durch isentrope Expansion

Der Gleichdruckprozess (bei Kolbenmotoren auch Dieselkreisprozess genannt) ist ein Vergleichsprozess für Maschinen, bei denen die Wärme bei konstantem Druck zugeführt wird. (isobar; bei Kolbenmotoren also nach dem oberen Totpunkt zu Beginn der Expansion). Dazu im Gegensatz steht der Gleichraumprozess (auch Otto-Kreisprozess genannt), bei dem die Wärme bei konstantem Volumen zugeführt wird (isochor; bei Kolbenmotoren im oberen Totpunkt).

Reale Motoren arbeiten technisch meist im Übergangsbereich zwischen idealem Gleichraum- und Gleichdruckprozess, für den speziell der gemischte Seiliger-Kreisprozess eine bessere Näherung liefert, der sich sowohl für Diesel- als auch Ottomotoren anwenden lässt.

Idealer Gleichdruckprozess

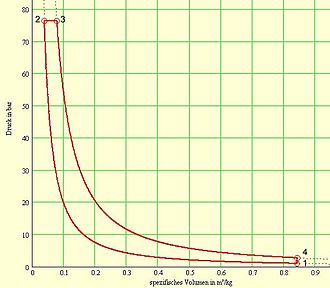
Thermodynamische Zustandsdiagramme eines idealen Gleichdruckprozesses (Dieselkreisprozess)
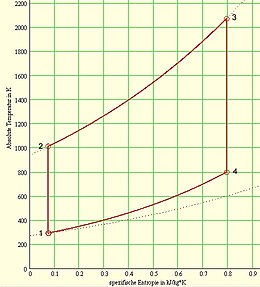
p-V-Diagramm (Isentropen punktiert gezeichnet)	T-s-Diagramm (Isobaren punktiert)

Der theoretisch ideale Gleichdruckprozess umfasst weder chemische Umsetzung (Verbrennung) noch Ladungswechsel mit Ausstoß von Abgas und besteht streng aus vier Zustandsänderungen eines idealen Gases innerhalb eines geschlossenen Systems:

1➝2: isentrope Kompression
2➝3: isobare Wärmezufuhr (deshalb Gleichdruckprozess)
3➝4: isentrope Expansion
4➝1: isochore Druckminderung durch Wärmeabfuhr (praktisch bei Motoren mit innerer Verbrennung durch Ladungswechsel, also Ausstoßen des Abgases und Ansaugen einer frischen Gasladung)

Die durch den Linienzug 1-2-3-4 umschlossene Fläche im p-V-Diagramm entspricht der spezifischen Prozessarbeit w.

Thermischer Wirkungsgrad beim Gleichdruckprozess

→ Hauptartikel: Thermischer Wirkungsgrad

Der Wirkungsgrad des Gleichdruckprozesses (Dieselprozess) ist abhängig von:

$\varepsilon ={\frac {V_{1}}{V_{2}}}$ ; geometrisches Verdichtungsverhältnis (Größtwert des Verbrennungsraumes bei Kolben im UT / Kleinstwert des Verbrennungsraumes bei Kolben im OT)

$\psi ={\frac {V_{3}}{V_{2}}}$ ; Volldruck- oder Gleichdruck- oder Einspritzverhältnis

$\kappa ={\frac {C_{p}}{C_{V}}}={\frac {c_{p}}{c_{V}}}$ ; Isentropenkoeffizient des Arbeitsgases. Dieser Koeffizient wäre für Luft bei Normaltemperatur 1,4. Abgas bzw. Brenngas hat wegen veränderter Zusammensetzung und hoher Temperatur einen Wert von etwa 1,3. C ist die Wärmekapazität in J/K und c ist die Spezifische Wärmekapazität in J/(kg K).

$\psi ={\frac {H_{u}}{m_{H}c_{p}T_{1}\varepsilon ^{\kappa -1}}}+1$ ; Das Gleichdruckverhältnis ist abhängig von der Wärmezufuhr. Je größer die Wärmemenge, desto geringer der Wirkungsgrad!

$T_{1}$ : Grundtemperatur (K). Zum Beispiel 400 K (ca. 127 °C) vor dem Verdichtungstakt im Zylinder.

$H_{u}$ : zugeführte spezifische Heizenergie (J/kg). Zum Beispiel 42'000 J/kg für Diesel.

$m_{{H}}$ : spezifische Heizmasse pro Brennstoffmasse (kg/kg). Zum Beispiel 21 kg Luft und Restabgas pro kg Diesel.

${c_{p}}$ : spezifische Wärmekapazität der Abgase bzw. Brenngase in J/(kg K). Zum Beispiel 1,2 J/(kg K).

Die Ableitung für die Wirkungsgradformel lautet folgendermaßen:

Die zugeführte isobare Wärmemenge in Joule ist:

$Q_{23}=C_{p}(T_{3}-T_{2})$ oder in Newtonmeter $\kappa \cdot p_{23}(V_{3}-V_{2})=Q_{zu}$

Die abgeführte isochore Wärmemenge ist:

$Q_{41}=C_{V}(T_{4}-T_{1})$ oder $(p_{4}-p_{1})V_{41}=Q_{ab}$

Der Energieverlustfaktor ist:

${\frac {Q_{ab}}{Q_{zu}}}={\frac {1}{\kappa }}\cdot {\frac {(p_{4}-p_{1})V_{41}}{p_{23}(V_{3}-V_{2})}}={\frac {\varepsilon }{\kappa (\psi -1)}}\cdot {\frac {p_{4}-p_{1}}{p_{23}}}$

Unter Verwendung der Polytropengleichung $pV^{\kappa }=const$ folgt:

${\frac {p_{4}-p_{1}}{p_{23}}}=\left({\frac {V_{3}}{V_{41}}}\right)^{\kappa }-\left({\frac {V_{2}}{V_{41}}}\right)^{\kappa }=\left({\frac {\psi }{\varepsilon }}\right)^{\kappa }-\left({\frac {1}{\varepsilon }}\right)^{\kappa }={\frac {\psi ^{\kappa }-1}{\varepsilon ^{\kappa }}}$

Der thermische Wirkungsgrad ist:

$1-{\frac {Q_{ab}}{Q_{zu}}}=1-{\frac {\varepsilon }{\kappa (\psi -1)}}\cdot {\frac {\psi ^{\kappa }-1}{\varepsilon ^{\kappa }}}$

$\eta _{th\,\mathrm {Gleichdruck} }=1-{\frac {1}{\varepsilon ^{\kappa -1}}}\cdot {\frac {\psi ^{\kappa }-1}{\kappa (\psi -1)}}$

Vergleich der Wirkungsgrade von Gleichdruck- und Gleichraumprozess

Der erste Faktor rechts der Gleichung entspricht dem Wirkungsgradverlust ${\varepsilon ^{1-\kappa }}$ des Gleichraumrozesses. Der zweite Teil ist der zusätzliche Effizienzverminderungsfaktor (> 1 gegenüber dem Gleichraumprozess).

Bei gleichem Verdichtungsverhältnis $\epsilon$ hat der Gleichdruckprozess also rein rechnerisch eine schlechteren thermischen Wirkungsgrad als der ideale Gleichraumprozess. Technisch ist aber insbesondere der Dieselkreisprozess in modernen Motoren besser kontrollierbar als der Gleichraumprozess (speziell Otto-Kreisprozess), so dass er mit höher tolerierten Prozess-Parametern in der Praxis letztlich einen besserer Wirkungsgrad erreicht.

Dieselkreisprozess

Ergänzt um einen Ladungswechsel mit innerer Verbrennung und Ausstoß von Abgas wird der Gleichdruckprozess für Kolbenmotoren als Dieselkreisprozess bezeichnet. Dazu zählen sowohl Zweitakt- als auch Viertakt-Hubkolbenmotoren, deren Takt jeweils aus einem Kolbenhub bzw. einer halben Kurbelwellenumdrehung besteht. Die Verhältnisse sind prinzipiell übertragbar auf Drehkolbenmotoren und Kreiskolbenmotoren.

Der ideale Dieselmotor

Der theoretisch ideale Dieselmotor hat keine Dissipationsverluste, mechanische Reibungsverluste, Hilfsaggregate, Zylinderkühlung oder Dichtigkeitsverluste. Das Arbeitsgas hat über den gesamten Kreisprozess gleiche Eigenschaften und keine Strömungsverluste. Der ideale Ladungswechsel erfolgt ohne Vermischung von Frischladung mit Abgas.

Für den Viertakt-Dieselmotor lassen sich die Kurvenzüge im Zustandsdiagramm den 4 Arbeitstakten wie folgt zuordnen (die Nummerierungen im Zustandsdiagramm sind nicht zu verwechseln mit den Arbeitstakten!):

Takt "Ansaugen" (0➝1): Füllung mit Luft als Frischladung
Takt "Verdichten" (1➝2): isentrope starke Kompression bis zum Erreichen der Zündtemperatur im oberen Totpunkt zündet den einspritzenden Kraftstoff (Selbstzündung)
Takt "Expandieren": zunächst (2➝3) isobare Expansion während der Wärmezufuhr durch fortgesetzte Gleichdruck-Verbrennung, danach (3➝4) leistet isentrope Expansion des heißen Abgases weiter Arbeit
Takt "Ausschieben" (4➝1): Abweichend vom idealen Gleichdruckprozess erfolgt nun im unteren Totpunkt keine isochore Druckminderung durch Wärmeabfuhr, sondern die Wärme $q_{{ab}}$ wird durch Öffnen des Auslassventils mit dem Abgas aus dem Arbeitsraum entlassen, wobei der Restdruck dynamisch in den Auspuff expandiert. Anschließend wird durch den Kolbenhub (1➝0) das restliche Abgas ausgeschoben.

Während der Viertakter eine komplette Kurbel-Umdrehung mit 2 Arbeitstakten für den Ladungswechsel benötigt, erfolgt dieser beim Zweitaktmotor sehr schnell komplett während dem Durchlaufen des unteren Totpunktes, so dass die Arbeitstakte "Ansaugen" (0➝1) und "Ausstoßen" (1➝0) einfach entfallen. Nicht dargestellt sind die technischen Vorgänge des Ladungswechsels im thermodynamischen Zustandsdiagramm für den idealen Gleichdruckprozess, wo sie praktisch im Punkt 1 kumulieren.

Zustandsdiagramm für einen realen Viertakt dieselmotor
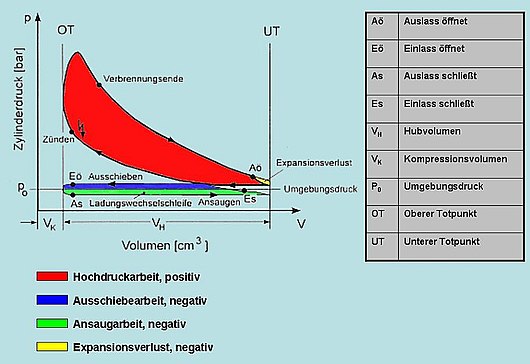
Kreisprozess eines Viertaktdieselmotors, schematisch im p-V-Diagramm	Viertaktdieselmotor: 1: Ansaugen; 2: Verdichten; 3: Expandieren; 4: Ausschieben

Der reale Dieselmotor

Vom Verlauf des theoretischen idealen Dieselkreisprozesses weichen die Zustandsänderungen beim realen Dieselmotor erheblich ab:

Das Kraftstoff-Luft-Gemisch ist kein ideales Gas, sondern hat einen kleineren Isentropenexponent und vergrößert seine Wärmekapazität bei hohen Temperaturen. Zudem verändert die Verbrennung die stoffliche Zusammensetzung, die Wärmekapazität des Arbeitsgases. Die Reaktionsprodukte Wasserdampf und Kohlendioxid haben andere thermodynamisch relevante Eigenschaften als Sauerstoff und Kraftstoff.

Isobare Wärmezufuhr wird praktisch nur näherungsweise erreicht, da der Verbrennungsvorgang (zeitliche Vermischung und Verbrennung des Treibstoffes mit der Luft) nicht genau an den sich mit der Kurbelbewegung verändernden Arbeitsraum angepasst wird: Wie im Otto-Motor führt auch im Dieselmotor die kurz vor dem oberen Totpunkt beginnende Wärmezufuhr zu einem weiteren Druckanstieg, so dass der Höchstdruck weit über den Verdichtungsdruck ansteigt.

Aus diesen Gründen hat der Gleichdruckprozess oder der Dieselkreisprozess wenig Vorhersagekraft für reale Motoren. Eine bessere Näherung als Gleichraum- und Gleichdruckprozess liefert der gemischte Seiliger-Kreisprozess, der sich sowohl für Diesel- als auch Otto-Motoren anwenden lässt.

Durch zeitgesteuerte Brennstoff-Einspritzung (Mehrfacheinspritzung bei Common-Rail-Motoren) kann auch die Verbrennung beeinflusst werden, um zu hohe Temperaturen und Drücke zu vermeiden.

Verluste beim realen Motor

Gegenüber dem Vergleichsprozess liefert der reale Kreisprozess im Motor eine geringere Arbeit:

Der Ladungswechsel mit Ansaugen und Ausschieben ist vergleichbar mit einem Pump-Vorgang, der durch Reibung und Strömungsverluste einen gewissen Teil der Motorleistung verbraucht (Ladungswechselarbeit = linksdrehende Schleife zwischen 0 und 1 im p-V-Diagramm).

Ein Teil der Wärmeenergie geht an den Brennraumflächen verloren und trägt nicht zur Arbeitsleistung bei. (Die Verluste durch unvollständige Verbrennung und endotherme Bildung von Stickoxiden werden im Vergleichsprozess nicht erfasst)

Da auch das Freigeben des Auslassquerschnitts einige Zeit benötigt, öffnet das Auslassventil schon kurz vor dem unteren Totpunkt, so dass die Prozessfläche im Punkt 4 angeschnitten wird (Expansionsverlust): Der Restdruck von typisch etwa 3-5 bar "verpufft" in die Abgasanlage, sofern nicht noch durch eine Abgasturbine dessen weitere Expansion genutzt wird.

Das Verhältnis der im Motor freigesetzten zu theoretischer Arbeit des Kreisprozesses wird als Gütegrad bezeichnet. Reale Motoren haben zusätzlich eine mechanische Verlustleistung durch Reibung, Neben- und Hilfsantriebe, die mehr als 10 % der Nennleistung betragen kann und den Wirkungsgrad mindert, besonders bei Teillast.

Technische Wirkungsgrade beim Dieselkreisprozess

Der thermodynamische Hauptverlust entsteht beim Dieselkreisprozess, wie auch beim Otto-Kreisprozess, durch nicht genutzte Abgaswärme und Abgas-Restdruck (typisch 3-5 bar), der beim einfachen Saugmotor ungenutzt in den Auspuff entlassen wird. Effektiver ist die weitere Expansion des Restdrucks in einer Abgasturbine, deren gewonnene Leistung vorzugsweise über einen Turbolader auf die Kurbelwelle übertragen wird, wenn im Ansaug-Takt die komprimierte Ladeluft den Kolben antreibt, statt wie beim Saugmotor gegen Unterdruck arbeiten zu müssen. Bei Großdieselmotoren kann Abgaswärme in einem Abhitzekessel zum Betrieb einer Dampfturbine genutzt werden.

Dieselmotoren mit Turbolader und Ladeluftkühlung erreichen so im Bestpunkt Wirkungsgrade von bis zu 42 % bei PKWs, 45 % bei LKWs und über 50 % bei großen Schiffsdieselmotoren, die ähnlich auch in Blockheizkraftwerken eingesetzt werden.

Die Abgaswärme hat einen wesentlicheren Anteil, als die Wärmeabfuhr durch Luft- oder Wasserkühlung. Beide Wärmeströme lassen sich gleichermaßen noch für Heizzwecke nutzen, vor allem bei stationären Anlagen wie Blockheizkraftwerken, aber auch auf Schiffen oder für Kraftfahrzeuge, die wegen schlechter Isolierung der Karosserie speziell im Winter einen erheblichen Heizwärme-Bedarf haben.

Siehe auch

Literatur

Wolfgang Kalide: Kolben und Strömungsmaschinen. 1. Auflage, Carl Hanser Verlag, München/Wien 1974, ISBN 3-446-11752-0.

Basierend auf einem Artikel in:

Wikipedia.de