Analytisches Signal

Ein analytisches Signal ist in der Signaltheorie eine komplexwertige Funktion der Zeit, dessen Imaginärteil die Hilbert-Transformierte des Realteils ist. Die Bezeichnung analytisch drückt aus, dass die Funktion im Komplexen differenzierbar ist (siehe analytische Funktion). Hieraus ergibt sich, dass im Spektrum eines analytischen Signals im Gegensatz zu einem reellen Signal keine negativen Frequenzen auftreten. Das analytische Signal stellt einen Spezialfall aus der Gruppe der monogenen Signale dar.

Anwendungen von analytischen Signalen in der Signalverarbeitung liegen im Bereich der Einseitenbandmodulation.

Definition

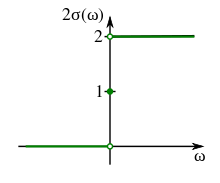
Übertragungsfunktion, durch die ein analytisches Signal gebildet wird.

Ist x(t) ein reelles Zeitsignal mit seiner Fourier-Transformierten X(jω), dann kann daraus ein Spektrum X_a(jω) mit rein positiven Frequenzen gewonnen werden, indem eine Multiplikation mit der Sprungfunktion σ(ω) erfolgt.

${\begin{aligned}X_{a}(\mathrm {j} \omega )&=X(\mathrm {j} \omega )\cdot 2\sigma _{\frac {1}{2}}(\omega )\\&=X(\mathrm {j} \omega )+X(\mathrm {j} \omega )\cdot \operatorname {sgn}(\omega )\end{aligned}}$

Dabei bezeichnet ω die Kreisfrequenz und j die imaginäre Einheit. Die inverse Fourier-Transformation $\mathcal{F}^{-1}$ erfolgt nach der Konvention der unsymmetrischen Normierung. Im Weiteren zeigt sich die Bildungsvorschrift für das analytische Zeitsignal x_a(t) aus dem Zeitsignal x(t).

${\begin{aligned}x_{a}(t)&=x(t)+{\mathrm {j}}\,x(t)\ast {\frac {1}{\pi t}}\\&=x(t)+{\mathrm {j}}\,{\mathcal {H}}\{x(t)\}\\&=x(t)+{\mathrm {j}}\,{\hat {x}}(t)\\\end{aligned}}$

Dabei stellen $\ast$ die $\mathcal{H}$ die Hilbert-Transformation dar. Bei einem analytischen Signal trägt der Imaginärteil in Bezug zu dem Realteil keinen zusätzlichen Informationsgehalt.

Beispiel

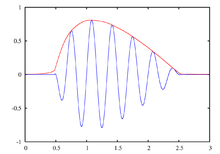
Das reelle Zeitsignal x(t), bestehend aus einer Cosinusschwingung, besitzt das analytische Signal x_a(t). Durch die Fourier-Transformation der eulerschen Identität zeigt sich, dass x_a(t) ein einseitiges Spektrum ohne negative Frequenzen besitzt.

${\begin{aligned}&x(t)=\cos(\omega _{0}t)&\Rightarrow \quad &x_{{\mathrm {a}}}(t)=\cos(\omega _{0}t)+{\mathrm {j}}\,\sin(\omega _{0}t)=e^{{{\mathrm {j}}\omega _{0}t}}\\&\Downarrow &&\Downarrow \\&X({\mathrm {j}}\omega )={\frac {\delta (\omega +\omega _{0})}{2}}+{\frac {\delta (\omega -\omega _{0})}{2}}&&X_{a}({\mathrm {j}}\omega )=\delta (\omega -\omega _{0})\\\end{aligned}}$

Darstellungen

Ein moduliertes Signal m(t) in blau und der Betragsverlauf A(t) des zugehörigen analytischen Signals

Wie jede komplexe Zahl kann das analytische Signal auch in komplexer Polardarstellung ausgedrückt werden.

$x_{{\mathrm {a}}}(t)=\underline \gamma (t)=A(t)e^{{j\varphi (t)}}\,$

Dabei wird γ(t) als die komplexe Einhüllende, A(t) als die Betragseinhüllende und φ(t) als die Momentanphase bezeichnet.

$A(t)=|x_{{\mathrm {a}}}(t)|={\sqrt {x^{2}(t)+{\hat {x}}^{2}(t)}}$

$\varphi (t)=\arg \left\{x_{{\mathrm {a}}}(t)\right\}$

System mit polarem Modulator

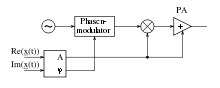
Von Bedeutung ist diese Darstellung in der Nachrichtentechnik, da sich damit ein polarer Modulator ansteuern lässt, wohingegen sich der Real- und Imaginärteil zum Ansteuern eines kartesischen Modulators (IQ-Modulator) eignet. Durch das Zusammenspiel mit einem entsprechend konstruierten Leistungsverstärker (englisch Power Amplifier abgekürzt PA), hat das erstgenannte System einen besseren Wirkungsgrad.

Ein moduliertes Signal m(t) wird dabei aus der Trägerfrequenz $\Omega _{T}$ und der komplexen Einhüllenden entsprechend der folgenden Gleichung erzeugt.

$m(t)=\Re \left(\underline \gamma (t)\cdot e^{{j\Omega _{T}t}}\right)=A(t)\cdot \cos(\Omega _{T}t+\varphi (t))$

Modulation

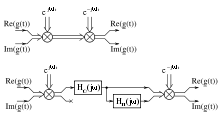
Modulation und Demodulation eines komplexen Signals

Durch Multiplikation lässt sich auf die Trägerfrequenz $\Omega _{T}$ ein komplexes Signal $\underline g(t)$ aufprägen, wodurch das komplexe modulierte Signal $\underline m(t)$ entsteht. Die Demodulation erfolgt durch Multiplikation mit einem komplexen Zeiger der in entgegengesetzter Richtung rotiert.

$\underline m(t)=\underline g(t)\cdot e^{{{\mathrm {j}}\Omega _{T}t}}$

$\underline g(t)=\underline m(t)\cdot e^{{-{\mathrm {j}}\Omega _{T}t}}$

$e^{{{\mathrm {j}}\Omega _{T}t}}\cdot e^{{-{\mathrm {j}}\Omega _{T}t}}=1$

Der Realteil und der Imaginärteil erfordern jeweils einen eigenen Übertragungspfad. In der Praxis wird oft darauf verzichtet. Durch Rechnung zeigt sich, dass es sich beim modulierten Signal m(t) um ein analytisches Signal handelt, also der Imaginärteil redundant zum Realteil vorliegt, womit auch nur einer von beiden übertragen werden muss.

$\underline m(t)=\left[\Re (\underline g(t))+{\mathrm {j}}\Im (\underline g(t))\right]\ \cdot \ \left[\cos(\Omega _{T}t)+{\mathrm {j}}\sin(\Omega _{T}t)\right]$

Vorausgesetzt bei x(t) handelt es sich um ein bandbegrenztes Signal, dessen Frequenzanteile oberhalb von $\omega _{0}$ eine Amplitude von null aufweisen, dann gilt folgende Hilbert-Transformation:

${\mathcal {H}}\{x(t)\cdot \cos(\omega _{0}t)\}=x(t)\cdot \sin(\omega _{0}t)$

$\underline m(t)=m(t)+{\mathrm {j}}{\mathcal {H}}\{m(t)\}$

Der Imaginärteil lässt sich Empfängerseitig durch die Hilbert-Transformation regenerieren.

$m(t)=\Re \left(\underline g(t)\right)\cdot \cos(\Omega _{T}t)-\Im \left(\underline g(t)\right)\cdot \sin(\Omega _{T}t)$

${\underline {g}}(t)=\left[m(t)+\mathrm {j} {\mathcal {H}}\{m(t)\}\right]\cdot e^{-\mathrm {j} \Omega _{T}t}$

Neben dem gezeigten Verfahren existieren weitere Möglichkeiten zum Erzeugen und Auflösen des gleichen modulierten Signals.

Basierend auf einem Artikel in:

Wikipedia.de