Stern-Dreieck-Transformation

Die Stern-Dreieck-Transformation oder Dreieck-Stern-Transformation, im englischen als Delta-Star-Transformation und als Kennelly-Theorem nach Arthur Edwin Kennelly bezeichnet, ist in der Elektrotechnik eine schaltungstechnische Umformung von jeweils drei elektrischen Widerständen, die der Schaltungsanalyse von Widerstandsnetzwerken dient. Die Stern-Dreieck-Transformation ist ein Spezialfall der Stern-Polygon-Transformation.

Allgemeines

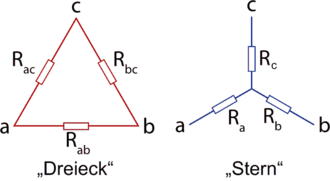
Stern-Dreieck-Transformation von Widerständen

Zur Verdeutlichung soll nebenstehende Abbildung dienen: Bei der Stern-Dreieck-Transformation wird die sternförmige (star) rechte Anordnung der Widerstände in eine dreieckförmige (delta) Widerstandsanordnung, links abgebildet, umgeformt. Die Dreieck-Stern-Transformation ist das Gegenstück dazu und ermöglicht die umgekehrte Umformung. Die elektrischen Anschlusswerte an den eingezeichneten Klemmen a, b und c bleiben dabei exakt gleich. Es werden bei dieser Transformation nur die drei Widerstandswerte durch geeignete Ersatzwerte für die neue Schaltungsanordnung ausgetauscht.

Durch entsprechende Anwendung dieser beiden Transformationen und der Regeln für Parallelschaltung und Reihenschaltung von Widerständen können im Rahmen der Schaltungsanalyse vereinfachte Ersatzwiderstände komplizierter Widerstandsnetzwerke gebildet werden.

Die Stern-Dreieck-Transformation ist identisch mit der Pi-T-Transformation zwischen der π-Schaltung und der T-Schaltung, welche die Widerstände grafisch unterschiedlich anordnet und im Bereich der Nachrichtentechnik bei Filterschaltungen Anwendung findet.

Transformationsregeln

Zur Dreieck-Stern-Transformation sind zur Bestimmung der Ersatzwiderstände folgende Berechnungen notwendig:

$R_a = \frac{R_{ac}R_{ab}}{R_{ac} + R_{ab} + R_{bc}}$

$R_b = \frac{R_{ab}R_{bc}}{R_{ac} + R_{ab} + R_{bc}}$

$R_c = \frac{R_{ac}R_{bc}}{R_{ac} + R_{ab} + R_{bc}}$

Für die umgekehrte Stern-Dreieck-Transformation sind zur Bestimmung der Ersatzwiderstände folgende Berechnungen notwendig:

$R_{ac} = \frac{R_aR_b + R_bR_c + R_cR_a}{R_b}$

$R_{ab} = \frac{R_aR_b + R_bR_c + R_cR_a}{R_c}$

$R_{bc} = \frac{R_aR_b + R_bR_c + R_cR_a}{R_a}$

Herleitung der Transformationsregeln

Um zu verstehen, warum die Stern-Dreieck-Transformation funktioniert, ist es ratsam, die Herleitung der Transformationsregeln zu betrachten.

Für unsere Zwecke ist es wichtig, dass sich das Klemmenverhalten zwischen den jeweiligen Klemmen (a-b, b-c, a-c) nach der Transformation nicht verändert.

$\frac{U_{dab}}{I_{dab}} = \frac{U_{sab}}{I_{sab}}$

U_sab ist die Spannung an den Klemmen a-b im Stern und U_dab im Dreieck. Analog dazu gelten natürlich auch die übrigen Klemmen b-c und a-c.

Betrachtet man nun die Skizze der Dreiecks- bzw. Sternschaltung, kann man mit den Regeln der Reihenschaltung und Parallelschaltung die Widerstände zwischen den Klemmen bestimmen.

$\tilde{R}_{ab} = \frac{1}{\frac{1}{R_{ab}}+\frac{1}{R_{ac}+R_{bc}}}$

Bringt man den Doppelbruch auf den gleichen Nenner, kommt man auf folgende Gleichung:

$\tilde{R}_{ab} = \frac{R_{ab}R_{ac} + R_{ab}R_{bc}}{R_{ab}+R_{ac}+R_{bc}}$

Das Gleiche wird auch mit der Sternschaltung gemacht:

$\tilde{R}_{ab} = R_a + R_b$

und mit der Dreiecksschaltung gleichgesetzt.

$\frac{R_{ab}R_{ac} + R_{ab}R_{bc}}{R_{ab}+R_{ac}+R_{bc}} = R_a + R_b$

Wiederholt man diese Schritte für die Klemmen b-c und a-c, so erhält man folgende beide Formeln:

$\frac{R_{ac}R_{ab} + R_{ac}R_{bc}}{R_{ab}+R_{ac}+R_{bc}} = R_a + R_c$

$\frac{R_{bc}R_{ab} + R_{bc}R_{ac}}{R_{ab}+R_{ac}+R_{bc}} = R_b + R_c$

Löst man dieses Gleichungssystem nach R_a, R_b und R_c auf, erhält man die oben erwähnten Transformationsregeln.

Unter Stern-Polygon-Transformation ist eine alternative, auch für den hier behandelten Stern-Dreieck-Spezialfall gültige Herleitung angegeben. Dort folgen die Transformationsgleichungen aus einem einfachen Koeffizientenvergleich.

Merkhilfe Vor- und Rücktransformation

Es gibt eine leichte Merk-Regel für die Vor- bzw. Rücktransformation:

$\text{Dreieck-Stern-Transformation wird für }\Delta \to \text{Y}$

$R_{c} = \frac{R_{ac} \cdot R_{bc}}{R_{ab}+R_{bc}+R_{ac}}=\frac{\text{Produkt der Anliegerwiderstände }}{\text{Maschenumlaufwiderstand}}$

$\text{Stern-Dreieck-Transformation wird für Y}\to \Delta$

$R_{ac} = \frac{R_{a} \cdot R_{c}}{R_{b}}+R_{a}+R_{c}=\frac{\text{Produkt der Anliegerwiderstände}}{\text{verbleibender Widerstand}}+\text{Beide Anliegerwiderstände}$

Anwendung in der Wechselstromrechnung

Die Stern-Dreieck-Transformation wird auch in der komplexen Wechselstromrechnung angewendet. Allerdings mit der Einschränkung, dass sie für beliebige lineare Impedanzen in den Zweigen nur für eine Frequenz gilt. Die Stern-Dreiecks-Transformation ist für alle Frequenzen gültig, wenn alle Zweige nur Kapazitäten, nur Induktivitäten oder nur Widerstände enthalten. Die Stern- und Dreiecksschaltung sind in der Wechselstromtechnik somit keine äquivalenten Schaltungen, können aber für die Berechnung von Netzwerken mit nur einer Frequenz (z.B. 50 Hz) angewendet werden. Dabei werden statt der rein ohmschen Widerstände die komplexen Impedanzen in den Gleichungen eingesetzt. Die Transformation erfolgt analog.

Literatur

Dieter Nührmann: Das große Werkbuch Elektronik. Band 1: Tabellen, Mathematik, Formeln, Wechselstromtechnik, Mechanik, SMD-Technik, passive Bauelemente, Batterien, Solarzellen, EMV-Technik. 6., neu bearbeitete und erweiterte Auflage. Franzis, Poing 1994, ISBN 3-7723-6546-9.

Basierend auf einem Artikel in:

Wikipedia.de