Stern-Polygon-Transformation

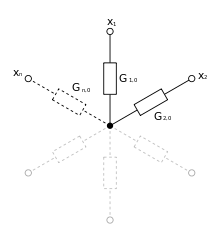
Sternschaltung
Jeder Anschluss ist über einen Widerstand mit dem Sternpunkt verbunden.

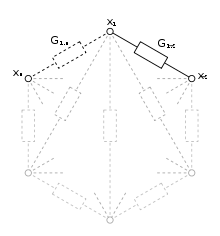
Polygonschaltung
Jeder Anschluss ist mit jedem anderen Anschluss über einen Widerstand verbunden.

Die Stern-Polygon-Transformation ist eine Verallgemeinerung der Stern-Dreieck-Transformation und wird in der Elektrotechnik angewendet, um eine Sternschaltung $n\geq 3;n\in \mathbb {N}$ elektrischer Widerstände in eine Polygonschaltung

${\frac {n\,\left(n-1\right)}{2}}$ elektrischer Widerstände zu wandeln, die sich bezüglich der Anschlüsse $X_{1},\dots ,X_{n}$ gleich verhält. Die umgekehrte Wandlung ist jedoch nur im Fall n=3

(d.h. bei der Stern-Dreieck-Schaltung) möglich.

Die Wandlung erfolgt aus der Beziehung der Leitwerte

$G_{i,j}={\frac {G_{i,0}\,G_{j,0}}{G_{s}}}$

mit dem Summenleitwert

$G_{s}=\sum _{i=1}^{n}{G_{i,0}}$ . Hierbei ist $G_{i,j}$ der Leitwert des Widerstands vom Anschluss $X_{i}$ zum Anschluss $X_{j}$ in der Polygonschaltung $G_{i,0}$ bzw. $G_{j,0}$ sind die Leitwerte des Widerstands vom Anschluss $X_{i}$ bzw. $X_{j}$ zum Sternpunkt in der Sternschaltung.

Sie gilt nicht für frequenzabhängige komplexe Impedanzen.

Herleitung

Die Transformationsgleichungen lassen sich aus der Bedingung herleiten, dass das Polygonnetzwerk an seinen Anschlusspunkten j=1 bis (entsprechend ${\text{X}}_{1}$ bis ${\text{X}}_{n}$ in den Skizzen) dieselben Ströme aufnehmen soll wie das Sternnetzwerk, wenn den Anschlusspunkten beider Netzwerke dieselben beliebig vorgebbaren Potenziale $\varphi _{j}$ eingeprägt werden. Das ließe sich praktisch mit Hilfe von zu einem Stern verbundenen Spannungsquellen erreichen. Die Summe der dem Sternpunkt zufließenden Ströme $\sum _{j=1}^{n}G_{j,0}(\varphi _{j}-\varphi _{0})$ ist nach dem Kirchhoffschen Knotensatz gleich null. Daraus folgt das Sternpunktpotenzial zu $\varphi _{0}={\frac {1}{G_{s}}}\sum _{j=1}^{n}G_{j,0}\varphi _{j}$ . Darin bezeichnet $G_{s}$ die Summe aller Sternleitwerte wie oben.

Der zum Sternpunkt durch einen ausgewählten Leitwert $G_{i,0}$ fließende Strom hat den Wert $I_{i}=G_{i,0}(\varphi _{i}-\varphi _{0})$ . Der in den entsprechenden Anschlusspunkt des Polygonnetzwerks eintretende Außenleiterstrom $I'_{i}=\sum _{j=1,~j\neq i}^{n}G_{i,j}(\varphi _{i}-\varphi _{j})$ ist gleich der Summe aller vom Anschlusspunkt abfließenden Ströme durch die Polygonleitwerte $G_{i,j}$ .

Mit der als Transformationsbedingung geforderten Gleichheit der Ströme (s. o.) $I_{i}$ und $I'_{i}$ folgt

$G_{i,0}(\varphi _{i}-{\frac {1}{G_{S}}}\sum _{j=1}^{n}G_{j,0}\varphi _{j})=\sum _{j=1,~j\neq i}^{n}G_{i,j}(\varphi _{i}-\varphi _{j})$ .

Auf der linken und rechten Seite der Gleichung steht jeweils eine Linearkombination aller Potenziale, über die ansatzgemäß frei verfügt werden kann. Die Gleichung ist für alle möglichen Potenzialwerte erfüllt, wenn jeder $\varphi$ -Koeffizient auf der linken Seite mit dem entsprechenden auf der rechten Seite übereinstimmt. Das Gleichsetzen der Koeffizienten von $\varphi _{j}$ liefert unmittelbar die oben angegebene Transformationsgleichung

${\frac {G_{i,0}G_{j,0}}{G_{s}}}=G_{i,j}$ .

Literatur

H. Haase, H. Garbe, H. Gerth: Grundlagen der Elektrotechnik. 4. Auflage. Schöneworth-Verlag Dähre, 2018, ISBN 978-3-9808805-5-8.

Basierend auf einem Artikel in:

Wikipedia.de