Parallelresonanz

Parallelresonanz, auch Stromresonanz, ist die Bezeichnung für das Impedanzmaximum elektronischer Schaltungen in der Umgebung einer Resonanzfrequenz. Parallelschwingkreise besitzen nur eine Resonanzfrequenz, andere Schaltungen mehrere.

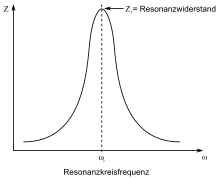
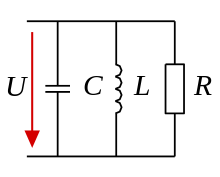
Maximum der Impedanz Z bei Parallelresonanz

Parallelschwingkreis

Diese hohe Impedanz wird beim Sperrkreis verwendet, um unerwünschte Frequenzen zu blockieren.

Das Gegenstück zur Parallelresonanz ist die Reihenresonanz.

Resonanz

Für den Betrag des frequenzabhängigen Scheinwiderstands |Z| einer Parallelschaltung aus R, L und C gilt nach den Grundlagen der Wechselstromtechnik:

$|Z| = \frac{1}{\sqrt{\frac{1}{R^2} + \left(\omega C - \frac{1}{\omega L} \right)^2}}$

Wenn der Term $\left(\omega C - \frac{1}{\omega L} \right)$ Null wird, ist der Scheinwiderstand der Parallelschaltung nach außen hin ein reiner, reeller Wirkwiderstand:

Die Parallelresonanz tritt auf bei

$\omega C = \frac{1}{\omega L}$

Obige Gleichung nennt man die Resonanzbedingung. Aus der Resonanzbedingung lässt sich durch Umformung und Auflösung von $\omega$ die Frequenz bestimmen, bei der die Resonanz eintritt, die Resonanzfrequenz $f_{r}$ . Sie ergibt sich aus der Thomsonschen Schwingungsgleichung:

$f_{r}={\frac {1}{2\pi }}{\frac {1}{\sqrt {LC}}}$

Weitere Eigenschaften bei Resonanz

Resonanzstrom

Durch die Blindwiderstände von L und C tritt bei Resonanz ein weiterer Effekt auf. Es fließen die folgenden Resonanzströme zwischen den beiden Bauelementen:

$I_{rC} = I_{rL} = \omega_r C U = \frac{U}{\omega_r L}$

Die Ströme erreichen für den Fall, dass

$\omega_r L = \frac{1}{\omega_r C} < R$

Werte, die größer sind als der von außen durch die Klemmenspannung getriebene Strom $I_r = \frac{U}{Z_r}$ . Aus dieser Schaltungseigenschaft resultiert die alternative Bezeichnung Stromresonanz für die Parallelresonanz.

Phasenwinkel

Der Phasenwinkel (Phasenverschiebung) $\varphi$ bei Resonanz beträgt

$\varphi_r = \arctan{\frac{0}{R}} = 0$

also keine Phasenverschiebung, da sich die Schaltung wie ein reiner Wirkwiderstand verhält.

Kreisgüte

Die Kreisgüte Q, auch Gütefaktor, Resonanzüberhöhung oder Resonanzschärfe, ist der Kehrwert des Verlustfaktors d. Für die Parallelschaltung von R, L und C erhält man:

$Q = \frac{1}{d} = R \omega_r C = \frac{R}{\omega_r L} = R \sqrt{\frac{C}{L}}$

Damit gibt sich für die Resonanzströme

$I_{rC} = I_{rL} = Q I_r$

Sonderfälle

Parallelresonanz von Spulen

Einlagige Zylinderspule

Spannungsverlauf längs einer Spule bei Parallelresonanz

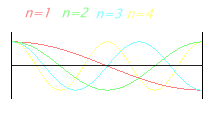
Spulen besitzen nicht nur zwischen den Anschlussdrähten eine geringe Kapazität, auch zwischen den einzelnen Windungen. Zusammen mit den dazwischen liegenden Induktivitäten entsteht ein Gebilde aus verteiltem L und C, das – ähnlich wie ein Dipol – mehrere Resonanzfrequenzen besitzt, die mit den Formeln der Leitungstheorie berechnet werden können.

Speist man eine lange Zylinderspule mit hochfrequentem Strom, kann man mit einem Oszilloskop die Spannung als Funktion der Länge messen. Folgt diese einer im Bild dargestellten Funktion, liegt Parallelresonanz vor, obwohl kein Kondensator erkennbar ist. Die Gesamtspannung zwischen den Spulenenden ist dann sehr groß, erheblich größer als der rechnerische Wert des induktiven Widerstandes.

Kreuzwickelspule mit geringer Eigenkapazität

Die tiefste Resonanzfrequenz kann durch eine besondere Wickeltechnik vergrößert werden. Bei einer Kreuzwickelspule ist der mittlere Abstand aufeinanderfolgender Windungen erheblich größer als bei üblicher Zylinderwicklung, wodurch sich die Kapazität aufeinanderfolgender Windungen verringert. Langgestreckte, einlagig gewickelte Zylinderspulen besitzen die höchste Eigenresonanzfrequenz. Bei sehr vielen Windungen, wie bei der Sekundärspule eines Tesla-Transformators, sinkt sie allerdings auf etwa 500 kHz.

Parallelresonanz bei Schwingquarzen

In vielen elektronischen Schaltungen ersetzt man wegen jener teilweise erheblich besseren Eigenschaften Schwingkreise durch Schwingquarze. Obwohl – abgesehen von parasitären Eigenschaften – diese Kristalle keine Spulen oder Kondensatoren besitzen, zeigen sie auf ganz speziellen Frequenzen alle Eigenschaften der Parallelresonanz; diese wird durch die Kombination von Piezoelektrizität und mechanischer Resonanz verursacht. Demzufolge kommt es auch auf (ungeradzahligen) Harmonischen zur Resonanz. Ausgehend von der tiefsten Frequenz verhalten sich die Resonanzfrequenzen ungefähr wie 1:3:5:7… Sie sind extrem stabil und weisen erheblich höhere Gütefaktoren als Schwingkreise auf, weshalb man Quarzoszillatoren als Taktgeber in Uhren und Sendern verwendet. Alle Schwingquarze zeigen Reihenresonanz auf einer geringfügig tieferen Frequenz.

Parallelresonanz bei Leitungen

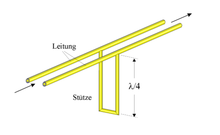
Die metallische Stütze isoliert die Doppelleitung bei bestimmten Frequenzen.

Bei Geräten im Radarbereich wird die Eigenschaft von Stichleitungen ausgenutzt, den Abschlusswiderstand abhängig von der Länge L zu transformieren (siehe Leitungstheorie). Streifenleitungen sind wegen der Permittivität des isolierenden Trägermaterials verkürzt.

Falls L = λ/2 und ein Ende offen ist, hat das andere Ende ebenfalls hohe Impedanz. Das gilt unverändert, wenn die Drahtlänge verdoppelt, verdreifacht oder allgemein ver-n-facht wird (n ∈ ℕ).
Falls L = λ/4 und ein Ende an Masse liegt, misst man am anderen Ende Parallelresonanz, also besonders hohe Impedanz. Das kurze Drahtstück ist bei dieser Wellenlänge genauso hochohmig wie ein Parallelschwingkreis. Das wird bei sehr hoher Frequenz verwendet, um eine Leitung wie mit einem Isolator zu stützen, obwohl diese Stütze für Gleichstrom sehr gut leitet.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de