Resonanzwiderstand
Der Resonanzwiderstand ist der Scheinwiderstand einer elektrischen Schaltung bei einer Resonanzfrequenz. Abhängig von der Schaltung der Bauelemente kann es auch mehrere Resonanzfrequenzen geben. Man unterscheidet zwischen Reihenresonanz mit besonders geringem und Parallelresonanz mit besonders großem Resonanzwiderstand.
Erläuterung
Elektronische Schaltungen enthalten immer auch Spulen und Kondensatoren als frequenzabhängige Blindwiderstände, damit man Signale unterschiedlicher Frequenz trennen kann. Deren Werte werden im Rahmen der komplexen Wechselstromrechnung als komplexe Zahlen angegeben, wobei die Imaginäranteile von Spulen und Kondensatoren entgegengesetzte Vorzeichen besitzen. Wenn sich bei gewissen Frequenzen diese Imaginäranteile kompensieren, liegt Resonanz vor.
Besonders einfache Verhältnisse ergeben sich, wenn die Schaltung ein Schwingkreis mit nur zwei Bauelementen ist:
- Bei einem Parallelschwingkreis sind die Spannungen an beiden Bauelementen gleich. Mit steigender Frequenz nimmt der Strom durch den Kondensator zu, wogegen der Strom durch die Spule sinkt. Bei einer ganz bestimmten Frequenz haben sie den gleichen Wert, aber entgegengesetzte Richtung. Dann kompensieren sich die Ströme und es fließt kein Gesamtstrom in den Zuleitungen zum Schwingkreis. Auf dieser Frequenz isoliert die Schaltung, was einem unendlich großen Resonanzwiderstand entspricht. Da die Phasenverschiebung von realen Bauelementen stets kleiner als 90° ist, kann man mit diesen keine perfekte Kompensation erzielen, weshalb der Resonanzwiderstand Werte von üblichen Isolationswiderständen nicht übersteigen kann.
- Bei einem Reihenschwingkreis sind die Ströme gleich und können einen beliebigen Wert annehmen. Verwendet man ideale, also verlustfreie Bauelemente, können sich bei einer ganz bestimmten Frequenz, der Resonanzfrequenz, die Spannungen an Spule und Kondensator kompensieren. Dann ist die Gesamtspannung Null, was einem frequenzselektiven Kurzschluss entspricht. Bei realen Bauteilen kann keine perfekte Kompensation erreicht werden, deshalb sinkt der Resonanzwiderstand bestenfalls in den Milliohm-Bereich.
Mitunter wird (falsch) vermutet, dass bei verschwindender Gesamtspannung auch beide Teilspannungen sehr gering sein müssen. Tatsächlich trifft aber das Gegenteil zu: Die Resonanzwandler in Scannern und Notebooks erzeugen mit Hilfe dieser Resonanzüberhöhung aus nur 12 V etwa 700 V Wechselspannung an den Anschlüssen von Spule und Kondensator zum Betrieb der Leuchtröhren.
Genauso falsch ist die Annahme, dass im Parallelschwingkreis bei Resonanz überhaupt kein Strom mehr fließt. Bei Resonanz kann durch die Spule ein erheblich höherer Strom als in der Zuleitung zum Schwingkreis fließen. Der Quotient beider Werte – der Gütefaktor – kann bei tiefen Frequenzen und einer verlustarmen Spule Werte um 100 erreichen, bei UKW-Frequenzen und einem versilberten Topfkreis sogar Werte über 1000.
Grundlagen
Allgemein
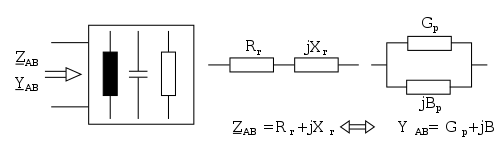
Ersatzschaltbild für komplexe Widerstände/Leitwerte: 1. Impedanz Z → 2. Admittanz Y
Wie bereits oben erwähnt, entsteht beim Durchfluss von Wechselstrom durch einen Leiter, eine Spule oder einen Kondensator neben dem ohmschen Widerstand R auch ein Blindwiderstand X, dessen Größe abhängig von der Frequenz und dem Verlauf des Wechselstromes ist. Um dies berechnen zu können, bedient man sich der komplexen Wechselstromrechnung, bei der man für den Widerstand R äquivalent die Impedanz Z und für den Leitwert G die Admittanz Y benutzt. Die Impedanz bzw. Admittanz beinhaltet sowohl den realen/ohmschen Anteil als auch den Blindanteil des Widerstandes oder Leitwertes. Die Impedanz und Admittanz sind, wie auch bei realem Leitwert und Widerstand, jederzeit ineinander umwandelbar. Unter Annahme idealer Bauelemente ist bei der Spule und beim Kondensator der reale Anteil (R bzw. G) null und beim Leiter/Widerstand der Blindanteil (X bzw. B) null. Dies wird der Einfachheit halber auch bei den meisten Berechnungen angenommen. Beim Resonanzwiderstand ist dies allerdings nicht möglich, da gerade diese Anteile den Resonanzwiderstand bestimmen.
Der Resonanzwiderstand ist also abhängig von den ohmschen Anteilen und vom Verlauf des Stromes. Der Verlauf beeinflusst ganz speziell die Resonanzfrequenz und den Blindwiderstand oder Blindleitwert und ist damit ein elementarer Bestandteil jeder Berechnung. Da der sinusförmige Verlauf in der Elektrotechnik die größte Bedeutung hat, wird in der Folge dieser Verlauf auch etwas genauer betrachtet.
Um Verwirrungen zu vermeiden, sollte vorher klar sein, dass wir zur Berechnung des Resonanzwiderstandes immer die Impedanz des gesamten Schwingkreises betrachten. Dies hat zur Folge, dass gerade bei parallelen Impedanzen der Realteil R (Wirkwiderstand) des gesamten Schwingkreises auch frequenzabhängig sein kann. Dies kann bei der Betrachtung von Impedanzen einzelner Bauelemente niemals passieren, da dort der Realteil immer und ausschließlich aus ohmschen Anteilen besteht.
Mathematisch
Im Allgemeinen entspricht der Resonanzwiderstand dem Scheinwiderstand bei
Resonanz. Der Scheinwiderstand entspricht dem Betrag der Impedanz.
Da im Fall der Resonanz der Blindwiderstand
Null wird, ist der Resonanzwiderstand
der Realteil der Impedanz.
Impedanz:
Scheinwiderstand:
Resonanzwiderstand: (Ist der Scheinwiderstand bei Resonanz)
Resonanzbedingung:
also (Blindwiderstand des Schwingkreises ist Null)
Daraus folgt
,
also
.
Es ist zu sehen, dass der Scheinwiderstand des Schwingkreises bei Resonanz, also der Resonanzwiderstand, nur durch den Wirkwiderstand repräsentiert wird. Man wird in der späteren Berechnung allerdings sehen, dass der Wirkwiderstand des Parallelschwingkreises, anders als der bei Bauelementen, frequenzabhängig ist und somit die Resonanzfrequenz eine entscheidende Rolle bei der Berechnung spielt.
Im Folgenden bedeutet:
= Blindwiderstand
= Wirkwiderstand
= imaginäre Einheit
= Impedanz des Kondensators
= Impedanz der Spule
= kapazitiver Blindwiderstand
= induktiver Blindwiderstand
= ohmscher Widerstand
= kapazitiver Verlustwiderstand
= induktiver Verlustwiderstand
Der Verlustwiderstand beinhaltet auch die Übergangswiderstände
und Leitungsverluste. Ein in Reihe geschalteter ohmscher Vorwiderstand wirkt additiv auf den Verlustwiderstand, also
Reihenschwingkreis
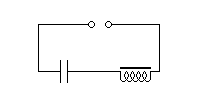
Der Reihenschwingkreis (auch Saugkreis genannt) besteht aus einer Spule und einem Kondensator, die in Reihe geschaltet sind. Der Resonanzwiderstand wäre bei idealen Bauelementen null, die Verlustwiderstände bzw. ein ohmscher Widerstand heben den Resonanzwiderstand jedoch an.
Allgemeingültige Formeln
Impedanz
Die Impedanz des Reihenschwingkreises ergibt sich folgendermaßen:
Herleitung:
Formel:
Resonanzfrequenz
Bei der Resonanzfrequenz des Reihenschwingkreises muss folgende Bedingung erfüllt sein:
Es ergibt sich:
Resonanzwiderstand
Für den Resonanzwiderstand gilt dann:
Für sinusförmige Verläufe
Resonanzfrequenz
Durch Einsetzen der Formeln für den Blindwiderstand kommt man zu:
Resonanzwiderstand
Es gilt die allgemeine Formel:
Anmerkung
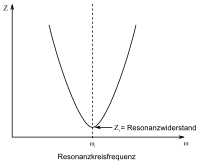
Es ist zu sehen, dass der Resonanzwiderstand den geringsten Widerstand eines Reihenschwingkreises darstellt. Der Resonanzwiderstand eines Reihenschwingkreises ergibt sich unabhängig vom Verlauf der Wechselspannung. Für Spulen und Kondensatoren mit hoher Güte ist der Einsatz eines ohmschen Vorwiderstandes unablässig, da die Verlustwiderstände dann im Verhältnis zum Innenwiderstand der Spannungsquelle so gering sind, dass sie im Resonanzfall praktisch einen Kurzschluss darstellen.
Parallelschwingkreis
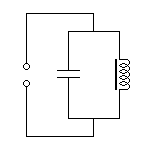
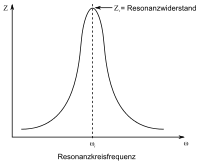
Der Parallelschwingkreis (auch Sperrkreis genannt) besteht aus einer Spule und einem Kondensator, die parallel geschaltet sind. Bei idealen Bauelementen wäre der Resonanzwiderstand unendlich hoch, die Verlustwiderstände senken den Wert des Resonanzwiderstandes allerdings deutlich.
Allgemeingültige Formeln
Impedanz
Die Impedanz des Parallelschwingkreises ergibt sich folgendermaßen:
Da
im Verhältnis zu
oftmals sehr klein ist, wird er zur Vereinfachung in der Regel vernachlässigt, so dass sich eine vereinfachte Formel für die Impedanz ergibt:
Resonanzfrequenz
Bei der Resonanzfrequenz des Parallelschwingkreises muss wiederum folgende Bedingung erfüllt sein:
Dies ist der Fall, wenn der Zähler gleich Null und der Nenner von Null verschieden ist: daraus folgt:
und
Resonanzwiderstand
Für den Resonanzwiderstand gilt dann:
Für sinusförmige Verläufe
Resonanzfrequenz
(Formeln siehe Blindwiderstand)
Die Formel für die Resonanzkreisfrequenz eines Parallelschwingkreises ist somit:
Wenn
ist, gilt die Thomsonsche Schwingungsgleichung.
Wenn
ist, beeinflussen die Verluste der Bauelemente die Resonanzfrequenz geringfügig, die Resonanzfrequenz wird gedämpft.
Wenn
und
angenommen wird, vereinfacht sich die Gleichung zu:
Im Fall, dass
und
ist, also bei der Annahme nur idealer Bauelemente, gilt diese Gleichung nicht, da in dem Fall auch der Nenner des Bruchs null würde, die Resonanzfrequenz wird in diesem
Fall nicht erreicht der Schwingkreis sperrt vorher vollständig.
Resonanzwiderstand
Als Vereinfachung kann man nun annehmen, dass
(Thomsonsche Schwingungsgleichung) und somit:
und
Damit folgt die Formel:
Da
in der Regel viel kleiner als
ist, kann man zur weiteren Vereinfachung
setzten, so dass nur noch folgendes übrig bleibt:
An dieser Formel ist sehr schön zu erkennen, dass der Verlustwiderstand der Spule den Resonanzwiderstand reduziert. Wäre
null, wäre der Resonanzwiderstand unendlich groß.
Anmerkung zu RL
Der in Reihe zur Spule geschaltete niederohmige
kann auch als hochohmiger parallel geschalteter Widerstand
beschrieben werden dabei gilt.
Für sinusförmige Wechselspannungen gilt dann:
Im Resonanzfall () ist:
was etwas weiter oben hergeleitet wurde. Da der eigentliche Resonanzkreis aus C und
bei Resonanz einen unendlichen Widerstand hat, ist die Impedanz
allein
.
Nach dem Einsetzen ergibt sich der Widerstand im Resonanzfall zu:
Der oben hergeleitete Ausdruck mit der Voraussetzung
gilt daher bei
auch ohne diese Einschränkung.
Anmerkung zu RC
Bei Kondensatoren wird der Verlust häufig als Verlustleitwert
anstelle des Verlustwiderstandes
angegeben. In diesem Falle nimmt man zur Darstellung nicht die Impedanz, sondern die
Admittanz, sprich den Verlustleitwert parallel
zum Blindleitwert.
Herleitung
Durch Umformung kommt man zu:
Formel
bzw.
Andere Resonanzwiderstände
Alle oben genannten Formeln gelten nur für Wellenlängen, die viel größer sind als die Abmessungen der Bauelemente. Unterschreitet die Wellenlänge einige Zentimeter, lassen sich Spulen und Kondensatoren entweder nicht mehr realisieren oder zeigen zusätzliche Eigenschaften, die das elektrische Verhalten drastisch modifizieren. Darüber hinaus werden Bauelemente eingesetzt, die weder Spulen noch Kondensatoren enthalten und trotzdem frequenzabhängige Impedanzen mit Resonanzeffekten zeigen.
Schwingquarz
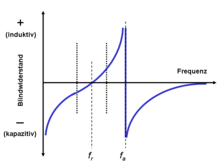
Misst man die Impedanz des Standardbauteils Schwingquarz über einen großen Frequenzbereich, ergibt sich eine eigenartige Gesetzmäßigkeit: In regelmäßigen Abständen können eng benachbarte Paare von Reihenresonanz fr und Parallelresonanz fa gemessen werden, deren Frequenzen sich jeweils um weniger als ein Prozent unterscheiden. Die genauen Werte werden durch die Abmessungen des Kristalls definiert und sind kaum veränderbar. Bildet beispielsweise fr1 = 5 MHz und fa1 = 5,003 MHz das erste Paar, folgt das zweite bei 15 MHz und das dritte bei 25 MHz.
Resonante Leitungen
Schaltungen im Bereich der Radarfrequenzen baut man oft als Streifenleitungen, wobei die Resonanzwiderstände besonderer Leitungslängen genutzt werden. Wird im nebenstehenden Bild Hochfrequenzenergie von links nach rechts geleitet, zeigt der λ/4-Streifen in einem engen Frequenzbereich Reihenresonanz und wirkt wie ein Saugkreis.
Literatur
- Edwin Wagner, Heinz-Ulrich Seidel: Allgemeine Elektrotechnik: Wechselstromtechnik - Ausgleichsvorgänge - Leitungen. 3. Auflage. Carl Hanser Verlag, 2005, ISBN 978-3-446-40018-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.08. 2025