Freiraumdämpfung

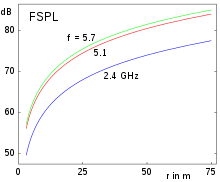
Freiraumdämpfung (FSPL, free-space path loss) in dB als Funktion der Entfernung für verschiedene Frequenzen

Die Freiraumdämpfung fasst zwei Terme der Leistungsübertragungsbilanz einer Funkverbindung zusammen: die Reduzierung der Leistungsdichte gemäß dem quadratischen Abstandsgesetz und die mit der Frequenz schrumpfende Wirkfläche einer Empfangsantenne ohne Antennengewinn. Sie ist das einfachste Modell für Pfadverluste, berücksichtigt nicht etwaige Dämpfung durch das Ausbreitungsmedium.

Die Ergänzung der Freiraumdämpfung um den Antennengewinn und die Sendeleistung zur Bildung einer Leistungsübertragungsbilanz wird als Friis-Übertragungsgleichung bezeichnet.

Der Freiraumdämpfungsfaktor wird in der Funktechnik üblicherweise logarithmisch als Freiraumdämpfungsmaß in dB ausgedrückt.

Berechnung

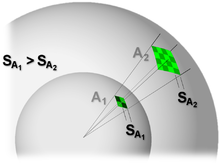
Leistungsdichte auf einer Kugeloberfläche

Da der Antennengewinn von Sende- und Empfangsantenne in der Leistungsbilanz gesondert auftaucht und sich auf den (theoretischen) Isotropstrahler bezieht, wird hier dessen Richtcharakteristik angesetzt. Für den Sender bedeutet das, dass sich seine hochfrequente Leistung gleichmäßig in alle Richtungen verteilt. Demzufolge bilden Flächen gleicher Leistungsdichte Kugeln um den Strahler. Bei größer werdendem Kugelradius verteilt sich die Leistung auf eine größere Fläche (Kugel) $A=4\pi r^{2}$ um den Strahler herum, die Leistungsdichte sinkt quadratisch:

(1) $S={\frac {P}{A}}={\frac {P}{4\pi r^{2}}}$

Der am Empfangsort näherungsweise ebenen Welle entnimmt die Empfangsantenne die Leistung

(2) $P_{\mathrm {r} }=SA_{\mathrm {W} }$

Darin ist für die Wirkfläche $A_{\mathrm {W} }$ die der isotropen Antenne einzusetzen. Sie hängt nur von der Wellenlänge $\lambda$ ab:

(3) $A_{\mathrm {W} }={\frac {\lambda ^{2}}{4\pi }}$

Setzt man (1) und (3) in (2) ein, so folgt:

$P_{\mathrm {r} }={\frac {P}{4\pi r^{2}}}{\frac {\lambda ^{2}}{4\pi }}=\left({\frac {\lambda }{4\pi r}}\right)^{2}P$

Das Verhältnis

$F={\frac {P}{P_{\mathrm {r} }}}=\left({\frac {4\pi r}{\lambda }}\right)^{2}$

der beiden Leistungen wird als Freiraumdämpfung bezeichnet und auch als Funktion der Frequenz $f={\frac {c}{\lambda }}$ angegeben:

$F=\left({\frac {4\pi rf}{c}}\right)^{2}$

mit der Lichtgeschwindigkeit .

Die Frequenzabhängigkeit der Freiraumdämpfung resultiert daraus, dass eine Leistung abgestrahlt, am Empfangsort aber eine Leistungsdichte betrachtet wird. Deswegen muss eine Flächeneinheit in die Gleichung eingehen, deren Dimension als Vielfaches der Wellenlänge angegeben werden kann (eine Folge aus Gleichung 3). Die Wellenlänge kann wiederum durch die Frequenz ausgedrückt werden, wodurch die Frequenzabhängigkeit entsteht. Die Freiraumdämpfung selbst ist dimensionslos, da die Flächeneinheit ins Verhältnis zur Kugeloberfläche gesetzt wird. Bei höherer Frequenz wird also die betrachtete Flächeneinheit $\lambda ^{2}$ kleiner, und das Verhältnis zur Kugeloberfläche $4\pi r^2$ verschlechtert sich.

Freiraumdämpfungsmaß

Das Freiraumdämpfungsmaß kann unmittelbar aus obiger Gleichung abgeleitet werden. Bei der Logarithmierung werden Exponenten zu Faktoren und Faktoren zu Summanden:

${\begin{alignedat}{2}F{\text{ in dB}}&=10\log _{10}F\\&=10\log _{10}\left({\frac {4\pi rf}{c}}\right)^{2}&&=10\log _{10}\left({\frac {4\pi r}{\lambda }}\right)^{2}\\&=20\log _{10}\left(r\cdot f\cdot {\frac {4\pi }{c}}\right)&&=20\log _{10}\left(r\cdot \lambda ^{-1}\cdot 4\pi \right)\\&=20\log _{10}(r/\mathrm {m} )+20\log _{10}(f/\mathrm {Hz} )+20\log _{10}\left({\frac {4\pi }{c}}\mathrm {\frac {m}{s}} \right)&&=20\log _{10}(r/\mathrm {m} )-20\log _{10}(\lambda /\mathrm {m} )+20\log _{10}\left(4\pi \right)\\&=20\log _{10}(r/\mathrm {m} )+20\log _{10}(f/\mathrm {Hz} )-147{,}55&&=20\log _{10}(r/\mathrm {m} )-20\log _{10}(\lambda /\mathrm {m} )+21{,}984\end{alignedat}}$

Beispiele

Mit dem Transceiver eines Kfz-Schlüssels mit $f=2{,}4\,\mathrm {GHz}$ (entsprechend der Wellenlänge $\lambda =125\,\mathrm {mm}$ ) und einer Leistung von etwa 4 mW (entsprechend 6 dBm) soll eine Entfernung von 5 m erreicht werden. Das Freiraumdämpfungsmaß beträgt ca. 54 dB. Antennengewinne sollen wegen der beiderseits angestrebten Rundstrahlcharakteristik nicht angesetzt werden. Damit beträgt der Empfangspegel −48 dBm entsprechend 13 nW.

Frequenz f	Abstand r	Freiraumdämpfung
Frequenz f	Abstand r	Faktor F	Maß in dB
0027 MHz	300 m (RC-Modell)	1,1·10⁵	051 dB
0100 MHz	100 km (UKW-Rundfunk)	1,8·10¹¹	112 dB
0013 GHz	30 km (Richtfunk)	,13·10¹⁴	144 dB
1575 MHz	25.000 km (GPS L1)	,13·10¹⁸	184 dB
0015 GHz	38.000 km (Rundfunksatellit)	,16·10²⁰	208 dB
0002,1 GHz	384.000 km (Mond–Erde, Apollo-Programm)	1,1·10²¹	211 dB
0008,4 GHz	500.000.000 km (Erde–Raumsonde Rosetta)	3,1·10²⁸	285 dB

Literatur

Jürgen Detlefsen, Uwe Siart: Grundlagen der Hochfrequenztechnik. 2. Auflage. Oldenbourg Verlag, München / Wien 2006, ISBN 3-486-57866-9
Hans Lobensommer: Handbuch der modernen Funktechnik. 1. Auflage. Franzis Verlag, Poing 1995, ISBN 3-7723-4262-0

Basierend auf einem Artikel in:

Wikipedia.de