Molmassenverteilung
Die Molmassenverteilung (engl. MWD, molecular weight distribution), auch Molekulargewichtsverteilung, selten Polymolekularität, beschreibt in Naturwissenschaft und Technik die Häufigkeitsverteilung einzelner Molekülmassen in Proben polymerer Stoffe. Die Breite dieser Verteilung wird durch die Polydispersität (auch Dispersität oder Polymolekularitätsindex) beschrieben. Eine Vielzahl an physikalischen, mechanischen und rheologischen Eigenschaften der Probe hängt von der Breite der Verteilung ab.
Synthetische hochpolymere Stoffe bestehen praktisch nie aus Molekülen einheitlicher Größe, sondern liegen in Form polymolekularer Gemische vor. Die Polymerisationsgrade der Moleküle (und somit auch deren Molmassen) sind über einen mehr oder weniger breiten Bereich verteilt.
Makromoleküle biologischen Ursprungs, z. B. Proteine oder DNA, haben hingegen häufig eine völlig einheitliche Molmasse.
Verteilungsfunktionen
Bei bestimmten Polymerisationen entsteht idealerweise eine Molmassenverteilung, die mathematisch mit einer
- Schulz-Flory-Verteilung, deren verallgemeinerte Form die Schulz-Zimm-Verteilung ist (tritt bei Polyaddition und Polykondensation, sowie bei klassischen Kettenpolymerisationen auf)
oder
- Poisson-Verteilung (tritt bei lebenden Polymerisationen auf)
beschrieben wird.
In der Praxis treten durch die finite Größe des einzelnen Monomers sowie Nebenreaktionen stets (und auch beabsichtigt) größere Abweichungen davon auf, die z.B. wie folgend beschrieben werden:
- enge Molmassenverteilung
- geringe Anzahl von Fraktionen und hohe Anzahl der Moleküle pro Fraktion bzw. relativ wenige und geringe Abweichungen vom Mittelwert, d.h. hohe Einheitlichkeit;
- breite Molmassenverteilung
- viele Fraktionen und kleine Anzahl der Moleküle pro Fraktion oder unregelmäßige Verteilung der Moleküle pro Fraktion bzw. relativ viele und hohe Abweichungen vom Mittelwert, d.h. hohe Uneinheitlichkeit (technisch oft wünschenswert).
- bimodale oder multimodale Verteilung
- mit zwei oder mehreren getrennten Maxima in der Verteilungskurve
Molmasse von Polymeren
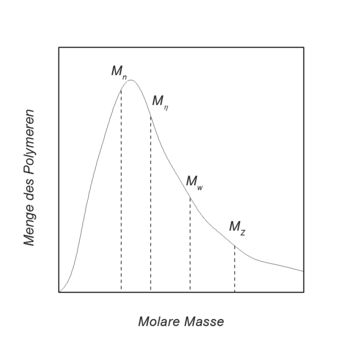
Es werden verschiedene Mittelwerte definiert, um die Probe statistisch zu beschreiben:
- Zahlenmittel der Molmasse
Die Molmasse
des i-mers wird mit dem relativen Zahlenanteil, den dieses Polymer hat,
gewichtet. Die zahlenmittlere Molmasse sagt also aus, welche Molmasse ein
zufälliges aus der Probe entnommenes Molekül im Durchschnitt hat. Dabei
entspricht
der Zahl an Makromolekülen in der Probe mit genau i Repetiereinheiten.
- Viskositätmittel der Molmasse
Das Viskositätsmittel
wird durch die Messung der Grenzviskositätszahl
der Polymerlösung ermittelt.
ist eine positive rationale Zahl und liegt in der Regel zwischen 0,5 und
0,9.
- Massenmittel der Molmasse
Die Molmasse
des i-mers wird mit dem relativen Massenanteil, den dieses Polymer hat,
gewichtet. Würde man eine zufällige Monomereinheit auswählen und die Molmasse
des dazugehörigen Polymers bestimmen, erhielte man als Durchschnitt die
gewichtsmittlere Molmasse.
- Zentrifugenmittel der Molmasse (Z-Mittel)
Das Zentrifugenmittel
wird durch Messung des Sedimentationsgleichgewichts ermittelt.
Abkürzungen:
: Molare Masse des Monomers
: Molare Masse der Polymere der jeweiligen Fraktion i
: Gesamtmasse der jeweiligen Fraktion i
: Anzahl der Makromoleküle in der Fraktion i
: Gesamtanzahl aller Fraktionen
=Stoffmenge [Masse] des i-mers;
=Summe aller
=Molenbruch des i-mers
=Molmasse des i-mers,
=mittlere Molmasse [Stoffmenge] einer monomeren Einheit
=Massenanteil des i-mers
Das Verhältnis aus Zahlenmittel
und der mittleren Molmasse einer monomeren Einheit
gibt den Polymerisationsgrad
(s.u.) an.
Bestimmungsmethoden
Die mittleren (s.o.) Molmassen einer Probe können mit verschiedenen Methoden bestimmt werden:
- Zahlenmittleres Mn
- kolligative Eigenschaften
- Kryoskopie
- Ebullioskopie
- Dampfdruckosmometrie bei geringen Molmassen (bis ca. 50.000 g/mol)
- Osmometrie bei sehr geringen Molmassen (bis ca. 10.000 g/mol)
- NMR-Spektroskopie
- kolligative Eigenschaften
- Sedimentationsanalyse zur Bestimmung des Zentrifugenmittels
- Viskosimetrie, d.h. rheologisches Verhalten in Lösung
- Rheologie
- Lichtstreuung
Aus den unterschiedlichen Werten können Rückschlüsse auf die Breite der Verteilung gezogen werden.
Zur direkten Bestimmung der Molmassenverteilung werden allgemein die
- Gelpermeations-Chromatografie (GPC) und
- Massenspektrometrie (MALDI-TOF) (für geringere Molmassen)
angewandt.
Die GPC benötigt dabei noch eine geeignete Kalibrierung, während MS eine Absolutmethode ist.
Die GPC und die Zentrifugation werden auch zur präparativen Polymerfraktionierung eingesetzt.
Polydispersität

Die Polydispersität Đ ist ein Maß für die Breite einer Molmassenverteilung, sie berechnet sich aus dem Verhältnis von Gewichtsmittel zu Zahlenmittel. Je größer Đ, desto breiter ist die Molmassenverteilung. Neben dem Formelzeichen Đ wird die Dispersität teilweise auch als Q, PDI (Polydispersitätsindex) oder Polymolekularitätsindex angegeben.
Anstatt der Polydispersität wird oft auch die molekulare
Uneinheitlichkeit
angegeben, sie ist definiert als
.
Makromoleküle biologischen Ursprungs, z.B. Proteine oder DNA, haben häufig eine völlig einheitliche Molmasse, sie haben also eine Uneinheitlichkeit von null, beziehungsweise Polydispersität von eins, daher gilt:
Für synthetische Polymere hingegen gilt:
Mittlerer Polymerisationsgrad
Allgemein erhält man den mittleren Polymerisationsgrad eines Homopolymers durch Division der mittleren molaren Masse durch die molare Masse der Wiederholeinheit. Diese kann im Einzelfall (z.B. bei Polykondensationen) von der des Monomeren abweichen.
Zahlenmittel
Gewichtsmittel
Viskositätsmittel
Literatur
- J. M. G. Cowie: Chemie und Physik der synthetischen Polymeren. Vieweg, 2 Ed., 1991.
- Bernd Tieke: Makromolekulare Chemie. Eine Einführung. Wiley-VCH, Weinheim 2005, ISBN 3-527-31379-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.04. 2024