
Magnetischer Kreis
Ein magnetischer Kreis ist ein geschlossener Pfad eines magnetischen Flusses Φ. Die Betrachtung magnetischer Kreise spielt vor allem in der Konstruktion von Elektromotoren, Transformatoren und Elektromagneten eine wesentliche Rolle. Hierbei sind vor allem Kopplungsprozesse zwischen den einzelnen Komponenten der magnetischen Kreise von Relevanz.
Elemente eines magnetischen Kreises
Bei einem magnetischen Kreis kann man zwischen zwei Signalarten:
- dem magnetischen Fluss und
- der magnetischen Spannung,
und drei grundlegenden Arten von Bauelementen:
- dem magnetischen Leiter
- dem magnetischen Widerstand mit dem Sonderfall des magnetischen Isolators und
- magnetischen Koppelelementen
unterscheiden.
Magnetischer Fluss

Der magnetische Fluss wird gewöhnlich mit einer Spule als Koppelelement in den magnetischen Kreis eingebracht. Seinem Namen entsprechend handelt es sich beim magnetischen Fluss um eine sogenannte "Flusskoordinate". Bei Verzweigungen des magnetischen Kreises verhält sich der magnetische Fluss entsprechend der kirchhoffschen Knotenpunktgleichung und teilt sich in die einzelnen Teilzweige auf.
Den Zusammenhang zwischen der elektrischen Spannung
und dem magnetischen Fluss
liefert das Induktionsgesetz
in der transformierten Darstellung mit komplexen Zahlen:
Dabei sind j die imaginäre Einheit, ω = 2πf die Kreisfrequenz und N die Windungszahl der Spule.
Magnetische Spannung Vm und magnetische Durchflutung Θ
Die magnetische Spannung ist als Linienintegral über die magnetische Feldstärke H zwischen zwei Punkten P1 und P2 entlang des Weges s definiert.
Die magnetische Spannung wird im Allgemeinen von elektrischen Strömen
hervorgerufen und über das Koppelelement Spule in den Magnetkreis eingebracht.
Dabei ist jedoch zu berücksichtigen, dass die elektrischen Ströme nicht eine
magnetische Spannung zwischen zwei Punkten, sondern eine sogenannte
magnetische Umlaufspannung oder magnetische Durchflutung
verursachen. Hierbei handelt es sich um eine magnetische Spannung entlang eines
geschlossenen Weges. Die magnetische Umlaufspannung bezeichnet man zur
Unterscheidung von der magnetischen Spannung mit dem Buchstaben
und schreibt
Die Besonderheit beim Vorhandensein einer Umlaufspannung besteht darin, dass die magnetische Spannung zwischen zwei Punkten von dem durchlaufenen Weg abhängt (nichtkonservatives Feld), so dass die kirchhoffsche Maschenregel für magnetische Spannungen im Allgemeinen nicht angewendet werden kann. Im Modell des magnetischen Kreises "rettet" man die Kirchhoffsche Maschenregel jedoch durch die Vereinbarung, dass bei der Anwendung der Maschenregel keine Integrationswege durch Spulenwicklungen betrachtet werden und vermeidet dadurch innere Widersprüche der Theorie.
Da die Koppelspule meist über einen magnetisch gut leitfähigen Spulenkörper
gewickelt wird, kann man zur Berechnung der magnetischen Spannung vereinfachte
Annahmen treffen. Denn wenn in dem Spulenkörper nur eine verschwindende
magnetische Feldstärke H herrscht, fällt der relevante Anteil der von den
Spulenströmen erzeugten magnetischen Spannung
ausschließlich außerhalb des Spulenkörpers ab.
Ein Spulenstrom ,
der einen magnetisch gut leitfähigen Spulenkörper N-mal umwickelt,
verursacht unter diesen Umständen außerhalb der Spule eine magnetische Spannung
der Größe
mit der in der Zeichnung angegebenen Bezugsrichtung.
Magnetische Leiter
Magnetisch gut leitende Verbindungselemente sind das Analogon zur metallischen Verbindungsleitung im elektrischen Stromkreis.
Magnetische Leiter sind dadurch gekennzeichnet, dass das Verhältnis aus der
magnetischen Spannung
und dem magnetischen Fluss
im magnetischen Leitermaterial nahezu gleich Null ist
Ein Beispiel für einen magnetischen Leiter ist der Magnetkern bei einem Transformator oder einer
Spule.
Die entscheidende Bedingung für magnetisch leitfähige Materialien ist ein hoher
Wert der relativen
Permeabilitätszahl .
Die relative Permeabilitätszahl gibt die magnetische Leitfähigkeit des
jeweiligen Stoffes im Vergleich zum Vakuum an. Typische Werte für ferromagnetische
Kernmaterialien in Spulen und Transformatoren liegen im Bereich
.
Magnetische Widerstände
Verbindungselemente aus magnetisch schlecht leitenden Materialien wie paramagnetischen oder diamagnetischen Materialien heißen magnetische Widerstände.
Magnetische Widerstände sind dadurch gekennzeichnet, dass das Verhältnis aus
der magnetischen Spannung
und dem magnetischen Fluss
eine endliche reelle Zahl
ist.
Sie sind das Analogon zum elektrischen
Widerstand. Ein Beispiel für einen magnetischen Widerstand ist eine kurze
Unterbrechung des magnetischen Kernmaterials eines Transformators durch einen
Luftspalt. Supraleiter haben eine Permeabilitätszahl
und sind demzufolge ideale magnetische Isolatoren.
Elektrische Spule als magnetisches Koppelelement
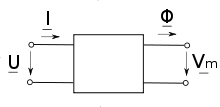
Mithilfe von Koppelelementen kann man die Wirkung von Netzwerken aus anderen physikalischen Gebieten in den Magnetkreis einbringen. Ein besonders häufig verwendetes Koppelelement im Magnetkreis ist die elektrische Spule. Sie verknüpft elektrische Stromkreise mit dem magnetischen Kreis und überträgt Energie zwischen beiden Netzwerken.
Die Kopplungsmatrix zwischen den elektrischen Größen und den magnetischen Größen ergibt sich zu:
Hierbei ist
die imaginäre Einheit,
die Kreisfrequenz und
die Windungszahl der Spule. Der Ausdruck
bezeichnet in zeitabhängiger Darstellung das Zeitintegral der elektrischen
Spannung - die sogenannte Spannungszeitfläche.
Da die elektrische Spule
- eine elektrische Potentialgröße (
) in eine magnetische Flussgröße (
) und
- eine elektrische Flussgröße (
) in eine magnetische Potentialgröße (
)
überführt, sagt man auch, die Spule sei ein gyratorisches Koppelelement.
Um die Wirkung von elektrischen Bauelementen auf den Magnetkreis zu verstehen, kann man die elektrischen Größen mithilfe der Transformationsgleichungen für die Spule in magnetische Größen umrechnen.
Transformation eines ohmschen Widerstandes
Im Falle eines elektrischen Widerstandes R liegt ein konstantes Verhältnis
aus elektrischer Spannung
und elektrischem Strom
vor.
Mit Hilfe der Transformationsgleichungen ergibt sich an einer Spule mit N Windungen daraus eine magnetische Impedanz von:
Ein elektrischer Kurzschluss R=0 verursacht demzufolge einen magnetischen Leerlauf, während ein elektrischer Leerlauf einen magnetischen Kurzschluss verursacht. Die physikalische Ursache des magnetischen Kurzschlusses beruht dabei auf der Modellannahme, dass die Spule einen Spulenkörper mit hoher magnetischer Leitfähigkeit umschließt.
Es ist zu beachten, dass ein elektrischer Widerstand an der Spule zu einer
magnetischen Impedanz der Form
führt. Der ohmsche Widerstand an der Spule verursacht daher im magnetischen
Kreis keinen magnetischen Widerstand, sondern vielmehr eine magnetische
Induktivität
.
Die Autoren Süße, Burger und andere
bezeichnen den elektrischen Widerstand am Koppelelement Spule in etwas
allgemeingültigerer Darstellung als Wirbelstromelement und führen aus:
Während der elektrische Widerstand
ein Energieverbraucher ist, stellt der magnetische Widerstand
einen Energiespeicher dar. Entgegengesetzt dazu ist die Induktivität L ein
Energiespeicher, und das Wirbelstromelement (magnetische Induktivität
)
ein Energieverbraucher.
Transformation einer elektrischen Induktivität
Eine elektrische Induktivität L führt im Magnetkreis zu einem rein reellen magnetischen Widerstand mit positivem Vorzeichen:
Transformation einer elektrischen Kapazität
Eine elektrische Kapazität C führt im Magnetkreis zu einem rein reellen magnetischen Widerstand mit negativem Vorzeichen:
Prinzipiell können auch Koppelelemente zu anderen physikalischen Gebieten wie
der Mechanik definiert werden. So bewirkt beispielsweise die Änderung
des magnetischen Flusses in einem magnetischen Kreis mit Luftspalt eine
Kraftänderung
auf die sich gegenüberstehenden Polflächen.
Analogie zum elektrischen Stromkreis
Die Gesetze des magnetischen Flusses sind analog zu den Gesetzen im
elektrischen Stromkreis definiert. Der magnetische Fluss Φ wird
hierbei analog zum elektrischen
Strom I, die Reluktanz
Rm analog zur Resistanz
R, und die magnetische
Spannung
analog zur elektrischen
Spannung U betrachtet.
In Analogie zum elektrischen Widerstand kann man im magnetischen Kreis den sogenannten magnetischen Widerstand
definieren.
In vielen magnetischen Materialien ist der magnetische Widerstand näherungsweise konstant. Man spricht in diesem Zusammenhang von dem ohmschen Gesetz des magnetischen Kreises
.
Die Reluktanz ist über die magnetische Leitfähigkeit und die geometrischen Abmessungen analog zur Resistivität definiert:
In magnetischen Kreisen, die durch konzentrierte Bauelemente beschrieben werden, gelten auch die kirchhoffschen Gesetze:
Über die kirchhoffschen Gesetze können magnetische Kreise berechnet werden.
| elektrische Größe | magnetische Größe | ||
|---|---|---|---|
| elektrische Spannung | U | magnetische Spannung | |
| elektrischer Strom | I | magnetischer Fluss | Φ |
| Resistanz (elektrischer Widerstand) |
R | Reluktanz (magnetischer Widerstand) |
Rm |
| Konduktivität (elektrische Leitfähigkeit) |
γ | Permeabilität (magnetische Leitfähigkeit) |
μ |
| Konduktanz (elektrischer Leitwert) |
G | Permeanz (magnetischer Leitwert) |
Gm |
Beispiele
Magnetischer Kreis mit Luftspalt
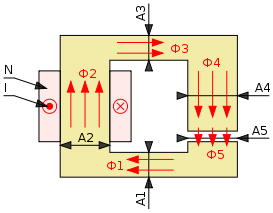
Die nebenstehende Abbildung zeigt den Aufbau eines einfachen magnetischen Kreises. Eine Wicklung mit N Windungen wird von einem elektrischen Strom I durchflossen und erzeugt damit die magnetische Flussdichte B2. Durch
erhält man den magnetischen Fluss im Kern der Wicklung. Der Kern dient der gezielten räumlichen Führung des magnetischen Flusses im magnetischen Kreis und wird aus Materialien mit hoher magnetischer Leitfähigkeit, wie beispielsweise als Ferritkern, ausgeführt.
In einem idealen ferromagnetischen Material ohne Streufluss gilt:
Da es in der Praxis jedoch keine ideal ferromagnetischen Materialien gibt, treten Verluste als Folge des Streuflusses auf. Die genaue Berechnung dieser Streuflüsse ist nur selten analytisch geschlossen zugänglich und sie erfolgt in der Regel über computerunterstützte numerische Näherungsverfahren. In der Praxis werden die Streuverluste an genormten magnetischen Kernen mit Hilfe vorher bestimmter Koeffizienten σ berechnet:
wobei V2,n die magnetische Spannungen der einzelnen Abschnitte darstellen.
Transformator mit zwei Wicklungen
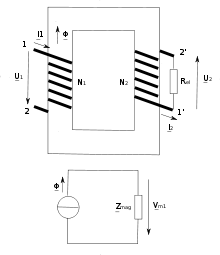
Im Modell des Magnetkreises ergibt sich der mit der Spannung
gespeiste Transformator mit der sekundärseitigen elektrischen Last
als ein einfacher Stromkreis, der mit dem magnetischen Fluss
gespeist wird.
Die magnetische Spannung ergibt sich entsprechend dem Bauelementegesetz für
die magnetische Impedanz
entsprechend zu:
Mit Hilfe der Gleichung
kann daraus der elektrische Strom in der Sekundärwicklung berechnet werden
,
was den bekannten Transformationsgleichungen für den Transformator entspricht.
Transformator mit zwei parallelen Lastkreisen

Die Vorteile bei der Modellierung, die in der Analogie zum elektrischen Stromkreis liegen, ergeben sich erst bei verzweigten Magnetkreisen.
Die Spannungsquelle
erzeugt einen magnetischen Fluss
der sich entsprechend der Knotenpunktgleichung für den magnetischen Kreis auf
die beiden Teilflüsse
und
aufteilt.
Die Aufteilung kann mithilfe der Stromteilerregel aus der Wechselstromrechnung berechnet werden. Für die beiden Teilflüsse ergibt sich:
Setzt man die Bauelementebeziehungen
und
ein, so ergeben sich daraus die Spannungen und die Ströme in den beiden passiven Wicklungen.
Für die Spannungen gilt:
und entsprechend
Aufgrund der Parallelschaltung ergeben sich identische magnetische Spannungen an beiden Teilzweigen:
Somit ergibt sich mithilfe von
für die Ströme:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.12. 2020