Gleichförmige Kreisbewegung
Eine gleichförmige Kreisbewegung ist eine Bewegung, bei der die Bahnkurve auf einem Kreis verläuft („Kreisbewegung“) und der Betrag der Bahngeschwindigkeit konstant ist („gleichförmig“). Sie ist damit eine Form der Rotation. Im Gegensatz zur gleichförmigen Bewegung bleibt nur der Betrag des Geschwindigkeitsvektors konstant, aber nicht seine Richtung.
Die einer Kreisbahn folgende Geschwindigkeitskomponente wird auch als Tangentialgeschwindigkeit oder Umlaufgeschwindigkeit bezeichnet. Die Radialgeschwindigkeit und Axialgeschwindigkeit haben bei einer einfachen Kreisbewegung den Wert Null.
Kreisbewegungen spielen oft eine Rolle in Bereichen der Kinematik und Dynamik.
Eigenschaften
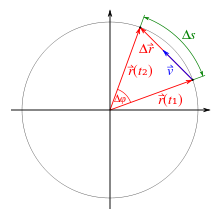
Eine Kreisbahn ist eine geschlossene Bahnkurve in einer Ebene mit konstantem Abstand zu einem Mittelpunkt. Die Wegstrecke stellt die Bogenlänge dar und ergibt sich aus dem Winkel und dem Radius.
Eine Bewegung auf der Kreisbahn lässt sich somit allein durch die Änderungsrate des Winkels, die Winkelgeschwindigkeit, beschreiben. Diese bleibt im Fall der gleichmäßigen Kreisbewegung konstant.
ist konstant
Somit ergibt sich der Betrag der Geschwindigkeit zu:
ist konstant.
Da die Bahnkurve geschlossen ist, kehrt die Bewegung stets zum selben Punkt zurück. Das dafür benötigte Zeitintervall wird als Umlaufdauer bezeichnet.
Vektorielle Betrachtung
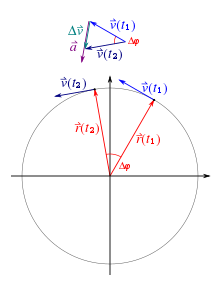
Der Geschwindigkeitsvektor ist wie bei jeder Bewegung tangential zur Bahnkurve, also hier tangential zum Kreis. Damit steht er senkrecht auf dem Radiusvektor. Er zeigt in Bewegungsrichtung.
Anhand der vektoriellen Betrachtung lässt sich auch die erforderliche Beschleunigung für eine Richtungsänderung ohne Betragsänderung der Geschwindigkeit ermitteln. Analog dem Vorgehen bei der Betrachtung des Geschwindigkeitsvektors erfolgt die Herleitung der Beschleunigung. Der Beschleunigungsvektor steht senkrecht auf dem Geschwindigkeitsvektor und zeigt zum Kreismittelpunkt.
Die Richtung der Beschleunigung ist damit geklärt nicht jedoch der Betrag. Hierbei hilft die Kleinwinkelnäherung, bei der die Bogenlänge zwischen den gleich langen Geschwindigkeitsvektoren zunehmend dem direkten Abstand zwischen den Vektorspitzen entspricht. Da sich die Winkeländerung der Kreisbewegung auch in den Geschwindigkeitsvektoren widerspiegelt, kann folgende Gleichsetzung der Grenzübergänge erfolgen:
.
Da der Beschleunigungsvektor immer Richtung Kreismittelpunkt zeigt trägt er die Bezeichnung Zentripetalbeschleunigung und in Verbindung mit der Masse gilt gleiches für die Zentripetalkraft.
Herleitung über Polarkoordinaten
Die Kreisbewegung eines Teilchen lässt sich effizient in Polarkoordinaten darstellen. In kartesischen Koordinaten ist
Dabei bezeichnet
den Abstand zwischen dem Ort des Teilchens und dem Ursprung, der das Zentrum der
Kreisbewegung ist und
den Winkel zwischen der Verbindungslinie von Ursprung und Ort des Teilchens und
der
-Achse.
Im Fall der Kreisbewegung ist der Radius konstant. Dann lautet die
Transformation in Polarkoordinaten:
Geschwindigkeit
Die Geschwindigkeit ist die Ableitung des Ortes. Dabei muss in Polarkoordinaten der Ortsvektor mitdifferenziert werden. Da der Abstand konstant ist, folgt
.
Die Ableitung des Einheitsvektor in -Richtung
ist proportional zu dem Einheitsvektor in
-Richtung,
da
orthogonal zu
ist. Für die Geschwindigkeit gilt damit
mit der Winkelgeschwindigkeit
.
Beschleunigung
Im Fall der Bewegungen ist der Betrag der Geschwindigkeit konstant. Wie im Fall der Geschwindigkeit reduziert sich die zeitliche Ableitung auf die Ableitung des Richtungsvektors. Die Beschleunigung der gleichförmigen Kreisbewegung lässt sich daher mittels
berechnen. Mit
folgt
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.05. 2021