Trenner (Graphentheorie)

Trenner sind in der Graphentheorie besondere Teilmengen von Knoten und Kanten eines Graphen, bei deren Entfernen aus dem Graphen bestimmte Wege im Graphen unmöglich werden.

Definition

Die Menge $S$ ist ein $A$ - $B$ -Trenner

Der Knoten $a$ ist ein Gelenkpunkt, die Kante $e$ ist eine Brücke.

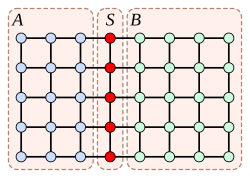
Es seien $G=(V,E)$ ein einfacher Graph und $A,B\subset V$ Teilmengen der Knotenmenge $V$ .

Ein Paar $Z=(X,Y)$ , bestehend aus einer Knotenmenge $X\subseteq V$ und einer Kantenmenge $Y\subseteq E$ , heißt $A$ - $B$ -Trenner oder $A$ - $B$ -Separator des Graphen, wenn jeder $A$ - $B$ -Weg wenigstens einen Knoten aus $X$ oder eine Kante aus $Y$ enthält. Man sagt dann auch, dass $Z$ die Knotenmengen $A$ und $B$ trennt.

Sind $A=\{a\}$ und $B=\{b\}$ einelementig, so spricht man auch von der Trennung der Knoten $a$ und $b$ .

Ein Paar $Z=(X,Y)$ trennt den Graphen $G$ genau dann, wenn $Z$ mindestens zwei Knoten aus $G$ trennt.

Äquivalente Definition

Teilweise wird in der Literatur ein $A$ - $B$ -Trenner für einen Graphen $G=(V,E)$ auch als eine Menge $X\subseteq V\cup E$ von Knoten und Kanten definiert, so dass jeder $A$ - $B$ -Weg mindestens ein Element aus $X$ enthält. Die weitergehenden Definitionen erfolgen analog zu den oberen.

Spezialfälle

Artikulation

Ist $v\in V$ ein Knoten, der zwei Knoten trennt, die zur selben Zusammenhangskomponente des Graphen gehören, so nennt man $v$ eine Artikulation, einen Gelenkpunkt oder einen Schnittknoten des Graphen. Einem Gelenkpunkt entspricht also ein Trenner $Z=(X,Y)$ mit $X=\{v\}$ und $Y=\emptyset$ .

Besitzt ein zusammenhängender Graph einen Gelenkpunkt, so ist seine Knotenzusammenhangszahl gleich 1 und er wird als separabel bezeichnet.

Brücke

Ist $e\in E$ eine Kante, die ihre beiden Endknoten trennt, so nennt man $e$ eine Brücke. Einer Brücke entspricht also ein Trenner $Z=(X,Y)$ mit $X=\emptyset$ und $Y=\{e\}$ . Äquivalent dazu ist, dass $e$ in keinem Kreis des Graphen liegt.

Besitzt ein zusammenhängender Graph eine Brücke, so ist seine Kantenzusammenhangszahl gleich 1.

Verwendung

Trenner gehören zu den Grundbegriffen der Graphentheorie. Sie werden beispielsweise verwendet, um die Grapheigenschaften k-Zusammenhang und Kantenzusammenhang zu definieren. In diesen beiden Fällen interessieren Trenner, die nur aus Knoten bzw. nur aus Kanten bestehen.

Literatur

Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (englisch, diestel-graph-theory.com – Sixth edition, 2025).

Basierend auf einem Artikel in:

Wikipedia.de