Spektrum (Graphentheorie)

Das Spektrum dient in der Graphentheorie zur Untersuchung der Eigenschaften von Graphen. Das entsprechende Gebiet wird als Algebraische Graphentheorie oder Spektrale Graphentheorie bezeichnet. Die Berechnung des Spektrums eines Graphen ermöglicht einen sehr effektiven Algorithmus zum Graphenzeichnen (Hall's Algorithmus.) Auch Expandergraphen können mittels spektraler Methoden charakterisiert werden.

Definition

Als Spektrum eines Graphen bezeichnet man die (nach Größe geordnete) Folge der Eigenwerte seiner Adjazenzmatrix. Letztere werden auch als Eigenwerte des Graphen bezeichnet.

(Ungerichtete Graphen haben eine symmetrische Adjazenzmatrix und deshalb reelle Eigenwerte.)

Graph	Adjazenzmatrix	Eigenwerte
	${\begin{pmatrix}0&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{pmatrix}}$	${\begin{pmatrix}\lambda _{1}=2.53948\ldots \\\lambda _{2}=1.08247\ldots \\\lambda _{3}=0.26114\ldots \\\lambda _{4}=-0.54063\ldots \\\lambda _{5}=-1.20607\ldots \\\lambda _{6}=-2.13639\ldots \\\end{pmatrix}}$

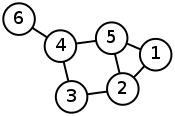Häufig werden auch die Eigenwerte der Laplace-Matrix des Graphen als sein Spektrum bezeichnet.

Beispiele

Die folgenden Beispiele beziehen sich auf das Spektrum der Adjazenzmatrix.

Der vollständige Graph auf Knoten hat das Spektrum

$(n-1,-1,-1,\ldots ,-1)$ .

Der vollständig bipartite Graph $K_{{mn}}$ hat das Spektrum

$({\sqrt {mn}},0,\ldots ,0,-{\sqrt {mn}})$ .

Ein Graph ist genau dann bipartit, wenn sein Spektrum symmetrisch bzgl. $0$ ist.
Der größte Eigenwert eines -regulären Graphen ist (Satz von Frobenius), seine Vielfachheit ist die Anzahl der Zusammenhangskomponenten des Graphen.

Basierend auf einem Artikel in:

Wikipedia.de