Schnitt (Graphentheorie)

Ein Schnitt bezeichnet in der Graphentheorie eine Partition der Knotenmenge eines Graphen. Eine besondere Bedeutung kommt Schnitten im Zusammenhang mit Netzwerken zu. Schnitte können aber auch unabhängig von Netzwerken definiert und untersucht werden.

Definition

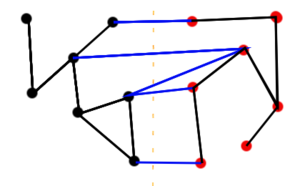
Knotenmenge $X$ (rot) und Restmenge $V\setminus X$ (schwarz) eines Schnittes und die kreuzenden Schnittkanten $E(X,V\setminus X)$ (blau)

Jede nichtleere Teilmenge $X\subset V$ der Knotenmenge eines ungerichteten Graphen $G=(V,E)$ definiert einen Schnitt $(X,V\backslash X)$ des Graphen.

Davon wird eindeutig die Menge der Schnittkanten

$E(X,V\backslash X)=\{(u,v)\in E:u\in X,v\in V\backslash X\}$

induziert. Sie umfasst alle Kanten des Graphen, von denen ein Endknoten in der Teilmenge $X$ liegt und der andere in der Menge der übrigen Knoten.

In gerichteten Graphen $D=(V,A)$ gibt es unterschiedliche Definitionen der Schnittkanten. Häufig verwendet man

$A(X,V\backslash X)=\{(u,v)\in A:u\in X,v\in V\backslash X\}$ .

Offensichtlich gilt hierbei im Unterschied zu ungerichteten Graphen, dass $A(X,V\backslash X)\neq A(V\backslash X,X)$ sein kann.

Eine andere Möglichkeit, Schnittkanten in gerichteten Graphen zu definieren, ist es, die Kanten in $A(X,V\backslash X)$ zunächst unabhängig von ihrer Orientierung aufzunehmen, so dass wiederum $A(X,V\backslash X)=A(V\backslash X,X)$ gelten würde. In diesem Fall würde $A$ in die beiden Teilmengen $A^{+}$ und $A^{-}$ zerfallen. Gilt dann, dass entweder $A^{+}=\emptyset$ oder $A^{-}=\emptyset$ , so spricht man von einem gerichteten Schnitt, d. h., es zeigen entweder alle gerichteten Kanten in die Menge $X$ hinein oder aus ihr hinaus.

Wichtige Sätze und Aussagen

Zusammenhang und minimale Schnitte

Würde man alle Kanten eines Schnitts $E(X,V\backslash X)$ aus dem Graphen $G$ entfernen, so würde es keinen Weg mehr zwischen $X$ und $V\backslash X$ geben. War der Graph vor dem Entfernen der Kanten des Schnitts zusammenhängend, ist er es nachher also nicht mehr.

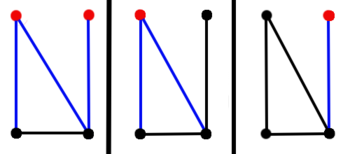
Der linke Schnitt ist nicht minimal, da die beiden rechten Schnitte in ihm enthalten sind

In diesem Kontext wird ein Schnitt auch als minimaler Schnitt bezeichnet, wenn nach dem Entfernen der Kanten des Schnitts aus dem Graph genau zwei Zusammenhangskomponenten entstehen. Das ist genau dann der Fall, wenn eine Knotenmenge $X$ so gewählt werden kann, dass der von ihr induzierte Schnitt keine Teilmengen an Kanten enthält, die einen von einer anderen Knotenmenge induzierten Schnitt bilden. Kurz gesagt: Ein Schnitt ist dann minimal, wenn nicht bereits eine Teilmenge des Schnitts einen Schnitt bildet.

Disjunkte Wege und Schnitte

Der Mathematiker Karl Menger stellte einen Zusammenhang zwischen knoten- und kantendisjunkten Wegen und Schnitten fest. Dieser Satz von Menger wurde später zum Max-Flow-Min-Cut-Theorem verallgemeinert.

Man betrachtet einen zusammenhängenden Graphen $G=(V,E)$ mit zwei Teilmengen der Knoten $S,T$ mit $S\subset V$ und $T=V\setminus S$ . Zwischen zwei Knoten $u,v$ mit $u\in S$ und $v\in T$ untersucht man die Anzahl der kantendisjunkten Wege sowie die Kardinalität (also Anzahl der Kanten) eines Schnitts $E(S,T)$ . Da alle kantendisjunkten Wege von $u$ nach $v$ durch den Schnitt müssen (denn das Entfernen der Kanten des Schnitts zerstört ja alle Wege von $u$ nach $v$ ) und, da die Wege kantendisjunkt sein müssen, jedes Mal eine andere Kante des Schnitts benutzt werden muss, gilt offensichtlich, dass die Kardinalität des Schnitts mindestens so groß sein muss wie die Anzahl kantendisjunkter Wege zwischen $u$ und $v$ . Menger zeigte schließlich, dass die maximale Anzahl kantendisjunkter Wege einer minimalen trennenden Kantenmenge genau entspricht.

Diese Erkenntnis gilt sowohl in gerichteten wie auch in ungerichteten Graphen. Sie lässt sich ferner von kantendisjunkten auf knotendisjunkte Wege übertragen und besagt dann, dass die maximale Anzahl knotendisjunkter Wege zwischen zwei Knoten $u$ und $v$ der Kardinalität einer minimalen trennenden Knotenmenge entspricht.

Damit besagt dann der k-Zusammenhang eines Graphen nicht nur, dass man mindestens $k$ Knoten entfernen muss, um den Zusammenhang zu zerstören, sondern auch, dass es zwischen zwei beliebigen Knoten eines Graphen auch immer mindestens $k$ knotendisjunkte Wege geben muss.

Schnitte und Kreise

Auch zwischen Schnitten und Kreisen gibt es einige Beziehungen. So muss die Kardinalität der Schnittmenge der Kanten eines Schnitts $E(S,T)$ und eines Kreises $C$ , also $|E(S,T)\cap C|$ gerade sein. Man stelle sich eine Kreiskante $e=(u,v)\in C$ vor, für die gilt, dass sie zusätzlich auch auf dem Schnitt liegt, also muss o. B. d. A. $u\in S$ und $v\in T$ sein. Wenn der Kreis nun in $u$ beginnen und dann $e$ nutzen würde, so kann die betrachtete Kante nicht die einzige Schnittkante von Kreis und Schnitt sein, da man nun in der Teilmenge $T$ ist und noch eine ungerade Anzahl von Schnittkanten zwischen Kreis und Schnitt benutzen muss, um wieder in die Teilmenge $S$ zurückzuwechseln, in welcher $u$ liegt. Insgesamt muss es also eine gerade Anzahl an Schnittkanten geben.

In einem zu $G$ dualen Graphen $G^{*}$ werden Schnitte zu Kreisen und Kreise zu Schnitten.

Starker Zusammenhang

Wenn ein gerichteter Graph $D=(V,A)$ stark zusammenhängend ist, kann man wiederum Knotenmengen $S\subset V$ betrachteten. Dann muss für alle möglichen Mengen $S$ gelten, dass der Schnitt $A^{+}(S,V\backslash S)\neq \emptyset$ ist. Nach der Definition von gerichteten Schnitten ist das gleichbedeutend mit der Aussage, dass es keinen gerichteten Schnitt geben darf. Denn bei "richtiger" Wahl von $S$ könnte es dann einen gerichteten Schnitt $A^{-}(S,V\backslash S)$ geben, was nach Definition heißen muss, dass $A^{+}(S,V\backslash S)=\emptyset$ ist, was aber der vorigen Aussage widersprechen würde.

Basierend auf einem Artikel in:

Wikipedia.de