Einschnürungssatz

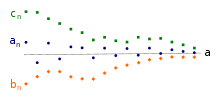
Sandwichsatz: Wenn eine Folge zwischen zwei konvergierenden Folgen mit demselben Grenzwert liegt, dann muss sie auch gegen diesen Grenzwert konvergieren.

Der Einschnürungssatz, Einschließungssatz, Dreifolgensatz oder Sandwichsatz (u.a.: Schachtelungssatz, Quetschlemma resp. Satz von den zwei Polizisten; englisch sandwich theorem) ist in der Analysis ein Satz über den Grenzwert einer Funktion. Gemäß dem Einschnürungssatz strebt eine Funktion, die von oben und unten durch zwei gegen denselben Wert strebenden Funktionen „eingezwängt“ wird, auch gegen diesen Wert.

Der Einschnürungssatz wird typischerweise dazu verwendet, einen Grenzwert einer Funktion nachzuweisen, indem man die Funktion mit zwei anderen vergleicht, deren Grenzwerte bekannt oder einfach zu bestimmen sind. Er wurde geometrisch schon von den Mathematikern Archimedes und Eudoxos verwendet, um die Kreiszahl π zu berechnen. Die moderne Formulierung des Satzes stammt ursprünglich von Carl Friedrich Gauß.

Der Satz gilt insbesondere auch für Grenzwerte von Folgen: eine Funktion, die von oben und unten durch zwei gegen denselben Wert strebenden Folgen beschränkt wird, konvergiert ebenfalls gegen diesen Wert.

Einschließungsregel für Folgen

Seien $x_{n}$ und y_n zwei reelle Folgen mit $x_n \rightarrow a$ , $y_n \rightarrow a$ und $x_n \leq y_n$ für fast alle (alle bis auf endlich viele) . Ist w_n eine weitere Folge mit $x_n \leq w_n \leq y_n$ für fast alle , so konvergiert w_n , und zwar ebenfalls gegen .

Beispiel

Sei

$w_{n}={\frac {1}{n+\log {n}^{2}+3}}$

eine Folge. Da $\log{n} \geq 0$ für $n\geq 1$ ist der Nenner immer größer als . Daher gilt

$0\leq w_{n}\leq {\frac {1}{n}}$ .

Da sowohl ${\frac {1}{n}}$ als auch $0$ gegen $0$ konvergieren, folgt aus der Einschließungsregel, dass w_n ebenfalls gegen $0$ konvergiert.

Einschnürungssatz für Funktionen

Es sei ein Intervall, das einen Wert enthält. Es seien , und auf $I\setminus\lbrace a\rbrace$ definierte Funktionen. Wenn für jedes $x\neq a$ aus gilt

$g(x) \leq f(x) \leq h(x),$

sowie

$\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L$ ,

dann ist $\lim_{x \to a} f(x) = L$ .

muss nicht inmitten von liegen. Ist Randpunkt von , so handelt es sich bei obigen Grenzwerten um links- bzw. rechtsseitige. Ähnliches gilt auch für unendliche Intervalle: Ist beispielsweise $I=[0,\infty)$ , so gilt der Satz auch für die Grenzwertuntersuchung $x\to \infty$ .

Zum Beweis folgt aus den Annahmen direkt

$L = \lim_{x \to a} g(x) \leq \liminf_{x \to a} f(x) \leq \limsup_{x \to a} f(x) \leq \lim_{x \to a} h(x) = L$ ,

so dass die Ungleichungen tatsächlich Gleichungen sind und daher auch gegen strebt.

Beispiele und Anwendungen

Die folgenden Beispiele zeigen, wie der Satz praktisch angewendet wird.

Beispiel 1

f (blau) mit Schrankenfunktionen g (rot) und h (grün)

Man betrachte $f(x) = x^2\sin\!\left(\tfrac{1}{x}\right)$ , das auf ganz $\mathbb {R}$ außer für x=0 definiert ist. Den Grenzwert für $x\to 0$ auf konventionelle Art zu berechnen fällt schwer: Eine direkte Substitution schlägt fehl, weil die Funktion bei x=0 nicht definiert ist (geschweige denn stetig), und die Regel von de l’Hospital kann auch nicht angewendet werden, da $\sin\!\left(\tfrac{1}{x}\right)$ überall oszilliert und keinen Grenzwert hat. Mit passenden oberen und unteren Schrankenfunktionen lässt sich jedoch der Einschnürungssatz anwenden.

Da die Sinusfunktion betragsmäßig durch 1 begrenzt ist, ist $x^{2}$ betragsmäßig eine passende Schranke für . In anderen Worten gilt mit g(x) = -x^2 und h(x)=x^2 :

$\begin{matrix} -1 &\leq& \sin\frac{1}{x} &\leq& 1 \\ -x^2 &\leq& x^2\sin\frac{1}{x} &\leq& x^2 \\ g(x) &\leq& f(x) &\leq& h(x) \end{matrix}$

und sind Polynomfunktionen und deshalb stetig, daher gilt

$\lim_{x \to 0} g(x) = \lim_{x \to 0} h(x) = 0$ .

Aus dem Einschnürungssatz folgt nun

$\lim_{x \to 0} f(x) = 0$ .

Beispiel 2

Das obige Beispiel ist eine spezielle Anwendung eines häufig auftretenden allgemeinen Falles. Angenommen, wir wollen zeigen, dass gilt:

$\lim_{x \to a} f(x) = L$ .

Es ist dann ausreichend, eine Funktion zu finden, die auf einem enthaltenden Intervall definiert ist (außer möglicherweise bei ), für die gilt

$\lim_{x \to a} h(x) = 0$ ,

und außerdem für alle $x\neq a$ aus gilt

$| f(x) - L | \leq h(x)$ .

In Worten gesprochen heißt das, dass der Fehler zwischen f(x) und beliebig klein gemacht werden kann, wählt man nahe genug an . Diese Bedingungen sind ausreichend, da die Betragsfunktion überall nicht negativ ist, so dass wir

für alle

wählen können und den Einschnürungssatz anwenden können. Da nun

für $x \to a$ gilt $|f(x) - L| \to 0$ ,

gilt auch $f(x) - L \to 0$ und damit

$f(x) = (f(x) - L) + L \longrightarrow 0 + L = L$ .

Beispiel 3

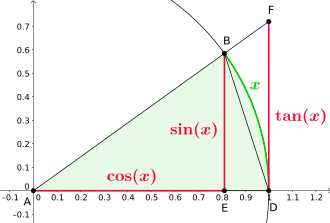
${\begin{aligned}&\,F(\triangle ADF)\geq F({\text{Sektor}}\,ADB)\geq F(\triangle ADB)\\\Rightarrow &\,{\frac {1}{2}}\cdot \tan(x)\cdot 1\geq {\frac {x}{2\pi }}\cdot \pi \geq {\frac {1}{2}}\cdot \sin(x)\cdot 1\\\Rightarrow &\,{\frac {\sin(x)}{\cos(x)}}\geq x\geq \sin(x)\\\Rightarrow &\,{\frac {\cos(x)}{\sin(x)}}\leq {\frac {1}{x}}\leq {\frac {1}{\sin(x)}}\\\Rightarrow &\,\cos(x)\leq {\frac {\sin(x)}{x}}\leq 1\end{aligned}}$

Durch elementargeometrische Überlegungen am Einheitskreis (siehe Zeichnung rechts) lässt sich zeigen, dass

$\cos(x) \leq \frac{\sin(x)}{x} \leq 1$ .

Wegen

$\lim_{x \to 0} \cos(x) = 1$

folgt mit dem Einschnürungssatz

$\lim_{x \to 0} \frac{\sin(x)}{x} = 1$ .

Dieser Grenzwert ist bei der Bestimmung der Ableitungsfunktion des Sinus behilflich.

Beweis

Die Hauptidee dieses Beweises ist es, die relativen Unterschiede der Funktionen , und zu betrachten. Dies hat den Effekt, dass die untere Schrankenfunktion konstant null ist, was den Beweis im Detail deutlich einfacher macht. Der allgemeine Fall wird dann auf algebraischem Wege bewiesen. Im Spezialfall g(x)=0 und L=0 gilt

$\lim_{x\to a} h(x) = 0$ .

Sei $\varepsilon >0$ ein fester Wert. Gemäß der Definition des Grenzwerts einer Funktion existiert nun ein $\delta >0$ , sodass

wenn gilt $0 < |x-a| < \delta$ , dann ist $|h(x)|<\varepsilon$ .

Für alle $x\neq a$ aus gilt gemäß Annahme

$0 = g(x) \leq f(x) \leq h(x)$ ,

also gilt

$|f(x)| \leq |h(x)|$ .

Daraus schließt man, dass

wenn gilt $0 < |x-a| < \delta$ , dann ist $|f(x)|\leq|h(x)|<\varepsilon$ .

Damit ist bewiesen, dass

$\lim_{x\to a} f(x) = 0$ .

Für beliebige und gilt nun für jedes $x\neq a$ aus

$g(x)\leq f(x)\leq h(x)$ .

Nun subtrahiert man g(x) von jedem Ausdruck:

$0\leq f(x)-g(x)\leq h(x)-g(x)$ .

Da für $x\to a$ sowohl g(x) also auch h(x) gegen streben gilt

$h(x)-g(x) \to L-L=0$ .

Mit dem oben bewiesenen Spezialfall folgt

$f(x) - g(x) \to 0$ für $x\to a$

und daraus dann

$f(x)=(f(x) - g(x)) + g(x) \to 0 + L = L$ .

Verallgemeinerungen

Eine maßtheoretische Verallgemeinerung ist der Satz von Pratt, bei dem durch die Einschnürung mittels lokal nach Maß konvergenten Funktionenfolgen auf die Vertauschbarkeit von Grenzwertbildung und Integration der eingeschnürten Funktionenfolge sowie auf die Integrierbarkeit der Grenzfunktion geschlossen werden kann.

Basierend auf einem Artikel in:

Wikipedia.de