Parallaktischer Winkel

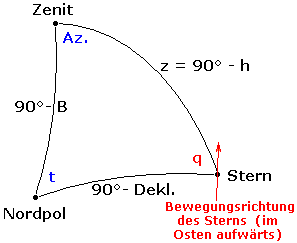
Astronomisches Dreieck mit seinen 3 Seiten (Kobreite 90°-B, 90°-Deklination, Zenitdistanz z) und den 3 Winkeln Azimut Az, Stundenwinkel t und parallaktischer Winkel q

Als parallaktischen Winkel q bezeichnet die sphärische Astronomie jenen Winkel des astronomischen Dreiecks (des Dreiecks Himmelspol-Zenit–Objekt), der am Objekt anliegt. Er gibt an, um welchen Winkel sich am Objekt die Richtung zum Himmelsnordpol von der Richtung zum Zenit des Beobachters unterscheidet.

Ein Objekt auf dem Meridian des Beobachters hat den parallaktischen Winkel q = 0°; für dieses Objekt liegen Himmelsnordpol und Zenit in derselben Richtung. Gemäß der üblichen Konvention hat das Objekt vor seiner Kulmination einen negativen und nach seiner Kulmination einen positiven parallaktischen Winkel. Für ein Objekt am Himmelsnordpol oder im Zenit ist der parallaktische Winkel undefiniert.

Fixsternbahnen

Der Winkel hängt mit der scheinbaren Bewegungsrichtung von Gestirnen auf ihrer täglichen Bahn am Himmel zusammen. Er ändert seinen Wert ständig, weil die Sternbahn gegenüber dem Horizont gekrümmt erscheint, und wird im Meridian zu Null: dort erreicht jedes Gestirn (ohne Eigenbewegung) seinen Höchststand und bewegt sich in diesem Moment horizontal.

Für Standpunkte auf dem Erdäquator gilt beim Auf- und Untergang jedes Sterns $q = \pm90^\circ$ , weil dort alle Gestirne senkrecht den Horizont überqueren (die Erdrotation „rollt“ den Beobachter quasi zum Stern bzw. von ihm weg).

Während sich bei uns die meisten Sterne nach rechts oben (Osthälfte des Himmels) bzw. nach rechts unten (Westhälfte) bewegen, haben Zirkumpolarsterne zweimal täglich auch senkrechte Bewegungsrichtung – nämlich für $q = \pm90^\circ$ . Diese Stellung heißt östliche und westliche Größte Digression, weil dort der Winkelabstand von Norden (das Azimut) seinen Maximalwert erreicht.

Bildfelddrehung

Während ein Himmelsobjekt im Zuge seiner „täglichen Bewegung“ (d.h. der Bewegung vom Aufgang über die Kulmination zum Untergang) über den Himmel wandert, ändert sich fortwährend sein parallaktischer Winkel. Ein Sternbild beispielsweise, welches sich in Nord-Süd-Richtung am Himmel erstreckt (etwa der Orion), wird während dieser Bewegung stets unverändert auf den Himmelsnordpol ausgerichtet bleiben. Es wird aber nur im Augenblick der Kulmination auch auf den Zenit ausgerichtet sein und damit für den Beobachter senkrecht stehen (q = 0). Beim Aufgang erscheint es einem Beobachter (auf der Nordhalbkugel) nach links geneigt (q < 0), beim Untergang erscheint es nach rechts geneigt (q > 0). Während die Ausrichtung des Sternbilds bezüglich der Nord-Süd-Richtung am Himmel also unverändert bleibt, ändert sich ständig seine Ausrichtung zur Vertikalrichtung des Beobachters.

Die Hochachse einer parallaktisch montierten Kamera ist auf den Himmelsnordpol ausgerichtet. Während einer nachgeführten Langzeitbelichtung bleibt das Sternbild für den Film stets „nach oben“ (also in Richtung Nordpol) ausgerichtet und kann problemlos fotografiert werden. Die Hochachse einer auf einem gewöhnlichen Fotostativ azimutal montierten Kamera ist hingegen auf den Zenit ausgerichtet. Für deren Film bleibt das Sternbild nicht „nach oben“ (also in Richtung Zenit) ausgerichtet, da sich seine Ausrichtung bezüglich des Zenits ständig ändert. Für diese Kamera dreht sich der Bildausschnitt während einer Langzeitbelichtung, so dass die Abbilder der Sterne zu Sternspuren auseinandergezogen werden.

Berechnung

Für einen Beobachter auf der geographischen Breite B und für einen Punkt an der Himmelskugel, welcher die Deklination δ und den Stundenwinkel t besitzt, kann der parallaktische Winkel q berechnet werden durch

$q = \arctan \left( \frac{\sin(t)}{\tan(B)\cos(\delta) - \sin(\delta)\cos(t)} \right)$

Falls der Nenner des Bruchs negativ ist, müssen zum Ergebnis 180° addiert werden, um den Winkel in den korrekten Quadranten zu bringen.

Herleitung

Zur Herleitung der Berechnungsformel betrachte man das sphärische Dreieck, dessen Ecken von dem betrachteten Punkt sowie dem Himmelsnordpol und dem Zenit gebildet werden (siehe Abbildung). Der am betrachteten Punkt anliegende Innenwinkel ist der parallaktische Winkel q.

Der Sinussatz der sphärischen Trigonometrie liefert die Beziehung

$\frac{\sin(90^\circ-B)}{\sin(q)} = \frac{\sin(z)}{\sin(t)}$

also

$\begin{align} \sin(z)\sin(q) & = \sin(90^\circ-B) \sin(t) \\ & = \cos(B) \sin(t) \end{align}$

Diese Formel könnte bereits nach dem gesuchten q aufgelöst werden. Durch die Kenntnis von sin(q) ist q jedoch noch nicht eindeutig bestimmt. q kann allen vier Quadranten des Vollkreises entstammen und es gibt im Vollkreis in der Regel zwei Winkel aus verschiedenen Quadranten, welche denselben Sinuswert haben, so dass die Bestimmung des Winkels aus dem bekannten Sinuswert nicht eindeutig ist. Die üblichen Implementierungen des arcussinus liefern denjenigen der beiden in Frage kommenden Winkel, welcher im Bereich -90° .. +90° liegt, so dass möglicherweise noch eine nachträgliche Korrektur in einen anderen Quadranten erforderlich wird.

Anstelle umständlicher geometrischer Überlegungen nutzt man in solchen Fällen meist den Umstand, dass ein Winkel sich eindeutig bestimmen lässt, wenn sein Sinus- und Kosinuswert bekannt sind. An deren Vorzeichenkombination lässt sich eindeutig der korrekte Quadrant erkennen.

Der Sinus-Kosinus-Satz liefert die Beziehung

$\begin{align} \sin(z) \cos(q) & = \cos(90^\circ-B) \sin(90^\circ-\delta) - \sin(90^\circ-B) \cos(90^\circ-\delta) \cos(t) \\ & = \sin(B) \cos(\delta) - \cos(B) \sin(\delta) \cos(t) \end{align}$

Division der beiden Gleichungen ergibt

$\begin{align} \tan(q) = \frac{\sin(z)\sin(q)}{\sin(z)\cos(q)} & = \frac{\cos(B)\sin(t)}{\sin(B)\cos(\delta)-\cos(B)\sin(\delta)\cos(t)} \\ & = \frac{\sin(t)}{\tan(B)\cos(\delta) - sin(\delta)\cos(t)} \end{align}$

Durch getrennte Betrachtung der Vorzeichen von Nenner und Zähler lässt sich der korrekte Quadrant ermitteln. Manche Programmiersprachen besitzen eine Variante der arcustangens-Funktion, welche dies automatisch erledigt (oft mit atan2 bezeichnet). Steht nur die übliche arcustangens-Funktion zur Verfügung, so berücksichtigt diese das Vorzeichen des Gesamtbruches. Der Benutzer muss dann noch 180° als Quadrantenkorrektur addieren, falls der Nenner der Bruchs negativ ist.

Der Faktor $\cos(B)$ durfte im Bruch gekürzt werden, weil die geographische Breite B aus dem Bereich -90°…+90° stammt und ihr Kosinus daher nicht negativ werden kann, das Kürzen also die Quadrantenbestimmung nicht beeinträchtigt.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de