
Disheptaeder
Ein Disheptaeder (auch Antikuboktaeder) ist ein Polyeder, das aus denselben Flächen wie das Kuboktaeder, also denen eines Hexaeders (Kubus) und eines Oktaeders, besteht. In dem Alternativnamen (Anti-Kubooktaeder) stecken entsprechend die Wörter Kubus und Oktaeder. Des Weiteren ist es als Johnson-Körper J27 (Dreiecksdoppelkuppel (verdrehtes Kuboktaeder)) bekannt.
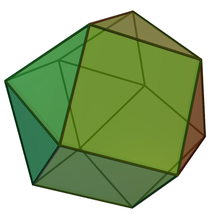
Beschreibung
Man erhält ein Disheptaeder aus einem Kuboktaeder durch Schnitt entlang der Ebene, die eine umlaufende Kante zwischen Hexaeder und Oktaederflächen bildet, und anschließende Verdrehung beider Hälften um 180° gegeneinander. Dadurch besitzen im Disheptaeder jeweils 3 Gruppen von je 2 Hexader- und 2 Oktaeder-Flächen eine gemeinsame Kante. Die vorherige Schnittebene wird zu einer Spiegelebene des Körpers.
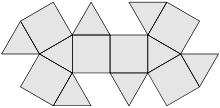
Mit 14 Flächen (8 gleichseitige Dreiecke
und 6 Quadrate),
12 Ecken und 24 Kanten gleicher Länge wird der eulersche
Polyedersatz
genau wie beim Kuboktaeder erfüllt.
Formeln
| Größen eines Disheptaeders mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| Kantenkugelradius | |
| 3D-Kantenwinkel = 120° |
|
Vorkommen
Das Disheptaeder findet in der Strukturchemie und Kristallographie als Koordinationspolyeder (z.B. in der hexagonal dichtesten Kugelpackung hcp) Verwendung. Die zugehörige Koordinationszahl ist (genau wie beim Kuboktaeder) 12; der Grenzradienquotient ist ebenfalls 1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.10. 2021