P-NP-Problem

Das P-NP-Problem (auch P≟NP, P versus NP) ist ein ungelöstes Problem der Mathematik, speziell der Komplexitätstheorie in der theoretischen Informatik. Dabei ist die Frage, ob die Menge aller Probleme, die schnell lösbar sind () und die Menge aller Probleme, bei der man eine vorgeschlagene Lösung schnell auf Korrektheit überprüfen kann (), identisch sind.

Es ist zwar klar, dass man bei allen schnell lösbaren Problemen auch schnell die Korrektheit einer Lösung überprüfen kann, in der umgekehrten Richtung ist dies jedoch nicht klar: Für manche Probleme existiert zwar ein Algorithmus, der eine vorgeschlagene Lösung schnell überprüfen kann, aber es konnte weder ein Algorithmus gefunden werden, der auch schnell eine korrekte Lösung findet, noch konnte die Unmöglichkeit eines solchen Algorithmus bewiesen werden. Somit ist die Fragestellung ungelöst. Würde man für alle schnell prüfbaren Probleme einen Algorithmus finden, der diese auch schnell löst, so gälte P=NP . Könnte für mindestens ein Problem aus gezeigt werden, dass dieses prinzipiell nicht schnell lösbar ist, wäre $P\neq NP$ bewiesen.

Ein Problem gilt in diesem Zusammenhang als schnell lösbar bzw. eine Lösung als schnell prüfbar, wenn ein Algorithmus existiert, bei dem der Anstieg des Rechenaufwands (Zahl der Rechenschritte) mit größer werdender Eingabe durch eine Polynomfunktion beschränkt ist und dieser Anstieg nicht etwa exponentiell verläuft. Die Größe der Eingabe ist hier vereinfacht gesagt die Anzahl der Elemente, die dem Algorithmus eingegeben werden. Bei einem Problem wie beispielsweise dem Sortieren von Karteikarten wäre dies die Anzahl der Karteikarten.

Geschichte

Erkannt wurde das Problem zu Beginn der 1970er-Jahre aufgrund unabhängig voneinander erfolgter Arbeiten von Stephen Cook und Leonid Levin.

Das P-NP-Problem gilt als eines der wichtigsten ungelösten Probleme der Informatik und wurde vom Clay Mathematics Institute in die Liste der Millennium-Probleme aufgenommen.

Wie später bekannt wurde, findet sich schon eine Formulierung des Problems in einem Brief von Kurt Gödel, den dieser an John von Neumann kurz vor dessen Tod schickte (am 20. März 1956). Eine weitere frühe Formulierung findet sich in einem Brief von John Forbes Nash 1955 an die National Security Agency, wobei es um Kryptographie ging.

P und NP

Die Komplexitätsklasse NP, unter der Annahme P≠NP. In diesem Fall enthält NP auch Probleme oberhalb von P, die nicht NP-vollständig sind.

Die Komplexitätstheorie klassifiziert Probleme, die von Computern berechnet werden können, anhand des zu ihrer Lösung erforderlichen Aufwands von Zeit oder Speicher, genauer: danach, wie schnell der Aufwand mit der Größe des Problems wächst. Ein Problem ist beispielsweise das Sortieren von Karteikarten. Es kann nun untersucht werden, wie sich die benötigte Zeit ändert, wenn ein doppelt so hoher Stapel sortiert wird.

Das hier genutzte Maß für den Berechnungsaufwand ist die Zahl der Rechenschritte, die der Algorithmus für ein Problem benötigt (Zeitkomplexität). Um den Berechnungsaufwand eindeutig anzugeben, werden außerdem formale Maschinenmodelle zur Darstellung der Lösungsalgorithmen benötigt. Ein häufig verwendetes Modell ist dabei die deterministische Turingmaschine, die als die Abstraktion eines realen Computers angesehen werden kann.

P

→ Hauptartikel: P (Komplexitätsklasse)

Eine der Problemkategorien ist die Komplexitätsklasse . Sie enthält die Probleme, für die eine deterministische Turingmaschine existiert, die das Problem in Polynomialzeit löst. Das heißt, es gibt ein Polynom $f(n)=n^{k}+c$ mit $c,k\in \mathbb {N}$ , so dass die Turingmaschine für keine Probleminstanz (mit Länge der Eingabe) mehr als f(n) Rechenschritte braucht. Probleme aus sind somit deterministisch in Polynomialzeit lösbar.

Das oben erwähnte Sortierproblem ist in P, weil es Algorithmen gibt, die eine Zahl von Datensätzen (Karteikarten) in einer Zeit sortierten, die durch eine quadratische Funktion in beschränkt ist. Ein weiteres Beispiel eines Problems in ist das Schaltkreis-Auswertungsproblem.

Der Unterschied zwischen einer Turingmaschine und realen Computern spielt hier keine Rolle, weil jeder Algorithmus, der auf einem realen Rechner ein Problem in Polynomialzeit löst, auch mit einer Turingmaschine in polynomieller Zeit realisiert werden kann (wobei aber der Grad des die Laufzeit beschränkenden Polynoms in der Regel höher sein wird).

NP

→ Hauptartikel: NP (Komplexitätsklasse)

Ein weiteres Maschinenmodell ist die nichtdeterministische Turingmaschine (NTM), sie ist eine Verallgemeinerung der deterministischen Variante. Eine NTM kann in einer Situation mehrere Möglichkeiten haben, ihre Berechnung fortzusetzen, der Rechenweg ist also nicht immer eindeutig bestimmt. Es handelt sich dabei um ein theoretisches Modell, es gibt keine real existierenden Computer, die ihren Rechenweg derart verzweigen können. Sein Nutzen ist in diesem Zusammenhang, dass damit eine weitere Komplexitätsklasse definiert werden kann, die viele Probleme von praktischem Interesse enthält, von denen man noch nicht weiß, ob sie in liegen.

ist definiert als die Menge der von einer NTM in Polynomialzeit lösbaren Probleme. Die deterministische Turingmaschine ist ein Spezialfall der NTM, sie verzichtet auf das Verzweigen des Rechenwegs. Darum ist eine Teilmenge von .

Man kann gleichbedeutend definieren als die Menge der Probleme, von denen sich in Polynomialzeit mit einer deterministischen Turingmaschine entscheiden lässt, ob eine vorgeschlagene Lösung zutrifft. Beispielsweise ist derzeit kein deterministischer Algorithmus bekannt, um eine gegebene Zahl in Polynomialzeit zu faktorisieren. Es ist jedoch sehr einfach prüfbar, ob ein vorgeschlagener Faktor die Zahl ohne Rest teilt und damit ein Faktor der Zahl ist.

Ist P=NP?

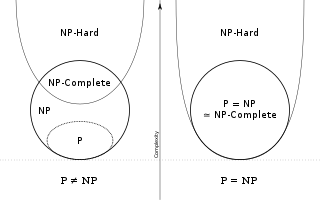
Beziehung der Probleme in P und NP und der NP-schweren und NP-vollständigen

Unbekannt ist, ob die beiden Klassen und identisch sind, ob also auch die schwersten Probleme der Klasse mit deterministischen Maschinen effizient lösbar sind. Um den Begriff des „schwersten Problems in “ formal zu fassen, wurden die Begriffe der NP-Vollständigkeit und der NP-Schwere eingeführt. Ein Problem X ist NP-schwer, wenn man jedes Problem in durch Polynomialzeitreduktion auf X reduzieren kann. Sollte man ein NP-schweres Problem X finden, das sich deterministisch in Polynomialzeit lösen lässt, könnte man auch jedes Problem in deterministisch-polynomiell lösen, indem man es auf X zurückführt, und es wäre $P=NP$ gezeigt. Ein Problem, das in liegt und NP-schwer ist, heißt NP-vollständig.

Ein anschauliches NP-vollständiges Problem ist das Rucksackproblem: Ein Behälter einer bestimmten Größe soll so mit einer Auswahl aus vorgegebenen Gegenständen gefüllt werden, dass der Inhalt so wertvoll wie nur möglich ist, ohne die Kapazität des Behälters zu überschreiten. Ein anderes wichtiges Beispiel ist das Erfüllbarkeitsproblem der Aussagenlogik.

Es wurde außerdem gezeigt: falls $P\neq NP$ ist und somit die NP-vollständigen Probleme nicht in liegen, dann gibt es in auch Probleme, die weder NP-vollständig noch in sind, die also in ihrer Schwierigkeit eine Zwischenstufe darstellen. Ein Kandidat für ein solches Problem ist das Graphen-Isomorphismus-Problem, von dem man bisher weder weiß, ob es in liegt, noch ob es NP-vollständig ist.

Lösung des Problems

Bisher sind zum exakten Lösen von NP-vollständigen Problemen nur Exponentialzeitalgorithmen auf deterministischen Rechenmaschinen bekannt. Es ist aber nicht bewiesen, dass es keine polynomzeitlichen Algorithmen für die Lösung gibt, im Gegensatz zu einer anderen Klasse von Problemen, die garantiert mindestens exponentielle Laufzeit benötigen (EXPTIME-vollständige Probleme) und die somit beweisbar außerhalb der Klasse liegen. Würde man für eines dieser NP-vollständigen Probleme für alle Eingaben einen auf deterministischen Rechenmaschinen polynomiell zeitbeschränkten Algorithmus finden (Klasse ), so könnte jedes beliebige Problem aus durch Polynomialzeitreduktion darauf reduziert und somit in deterministischer Polynomialzeit gelöst werden; in diesem Falle wäre also P=NP .

Da es bisher nicht gelang, einen solchen Algorithmus zu entwerfen, vermutet der Großteil der Fachwelt, dass $P\neq NP$ gilt. Dies könnte mathematisch dadurch nachgewiesen werden, dass für ein Problem aus der Klasse bewiesen wird, dass kein deterministischer Polynomialzeitalgorithmus zu dessen Lösung existiert.

Denkbare Szenarien für eine Lösung des Problems wären

Es wird bewiesen, dass $P\neq NP$ .
Es wird bewiesen, dass $P\neq NP$ logisch unabhängig von ZFC ist.
Es wird bewiesen, dass , indem für ein NP-vollständiges Problem ein effizienter Algorithmus angegeben wird.
Es wird mittels nicht-konstruktiver Techniken bewiesen, dass gilt, also ohne einen expliziten Algorithmus zu konstruieren.

Für die Komplexität des Problems spricht, dass bereits für verschiedene Beweistechniken gezeigt wurde, dass sie allein nicht ausreichend sind, um die Fragestellung zu klären.

Relativierende Beweistechniken

Ein Beweis für die Beziehung zweier Komplexitätsklassen ist relativierend, wenn die Beziehung für beliebig hinzugefügte Orakel erhalten bleibt. Unter die Klasse der relativierenden Beweistechniken fällt z.B. auch das in der Komplexitätstheorie häufig eingesetzte Verfahren der Diagonalisierung. Zeigt man beispielsweise $K \neq K'$ mittels Diagonalisierung, so gilt automatisch $K^A \neq K'^A$ für jedes Orakel . Der folgende wichtige Satz von Theodore Baker, John Gill und Robert Solovay beweist, dass relativierende Beweistechniken kein probates Mittel für das P-NP-Problem sein können und viele Angriffsmethoden auf das P-NP-Problem aus der theoretischen Informatik hierdurch ausfallen:

Es existieren zwei Orakel und , so dass $\operatorname{P}^A = \operatorname{NP}^A$ und $\operatorname{P}^B \neq \operatorname{NP}^B$ .

Natürliche Beweise

Alexander Alexandrowitsch Rasborow und Steven Rudich führten das Konzept der „natürlichen Beweise“ (engl. natural proofs) in ihrer gleichnamigen Arbeit von 1994 ein. Unter der allgemeinen vermuteten Annahme, dass bestimmte Einwegfunktionen existieren, zeigten sie, dass es nicht möglich ist, und durch eine bestimmte Sorte kombinatorischer Beweistechniken zu trennen.

Vereinfacht formuliert ist ein Beweis „natürlich“, wenn er ein Kriterium für „Einfachheit“ definiert und zeigt, dass Funktionen aus diese Eigenschaft haben und es ein NP-vollständiges Problem gibt, das diese Eigenschaft nicht besitzt. Das Kriterium für „Einfachheit“ muss hier zum einen für ausreichend große Menge von Funktionen gelten, zum anderen ausreichend einfach nachprüfbar sein.

Beweisversuche

Während das P-NP-Problem allgemein als ungelöst gilt, haben viele Amateure und professionelle Forscher verschiedene Lösungen veröffentlicht. Gerhard Woeginger betreibt eine Sammlung an Beweisversuchen, die im September 2016 62 angebliche Beweise für P=NP , 50 Beweise für $P\neq NP$ , zwei Beweise, dass das Problem nicht beweisbar ist, und einen Beweis, dass es unentscheidbar ist, auflistet. Unter all diesen Arbeiten gibt es nur eine einzige, die in einer peer-reviewed Zeitschrift erschienen ist, die von den Experten auf diesem Gebiet gründlich überprüft wurde und deren Korrektheit von der allgemeinen Forschungsgemeinschaft akzeptiert wird: Die Arbeit von Mihalis Yannakakis (dieses Paper klärt nicht die P-gegen-NP-Frage, sondern zeigt nur, dass ein bestimmter Ansatz zur Klärung dieser Frage niemals funktionieren wird).

In jüngerer Zeit bekanntgeworden ist der Beweisversuch für $P\neq NP$ vom 6. August 2010 des bei Hewlett-Packard angestellten Mathematikers Vinay Deolalikar. Er galt schnell als widerlegt, aber es gebührt ihm das Verdienst, sowohl in der Öffentlichkeit als auch in Fachkreisen das Thema zeitweise neu in den Fokus gerückt zu haben.

Praktische Relevanz

Sehr viele praktisch relevante Probleme sind NP-vollständig. Die Lösung des P-NP-Problems könnte daher von großer Bedeutung sein. Der Beweis von P=NP würde bedeuten, dass für die Probleme der Klasse Algorithmen existieren, die sie in Polynomialzeit lösen. Da jedoch in den vergangenen Jahrzehnten trotz intensiver Suche kein Algorithmus gefunden wurde, der ein NP-vollständiges Problem in Polynomialzeit löst, wird in der Fachwelt angezweifelt, dass solche Algorithmen überhaupt existieren, d.h., man geht von $P\neq NP$ aus.

Viele NP-vollständige Probleme, wie zum Beispiel das Problem des Handlungsreisenden, das Rucksackproblem oder das Problem der Färbung von Graphen, wären im Fall P=NP theoretisch optimal in kurzer Zeit lösbar. Allerdings könnten die Exponenten und Konstanten der Laufzeitfunktion eines polynomialen Verfahrens auch derart hoch sein, dass für praktisch relevante Anwendungen eines der bisher bekannten Lösungsverfahren, z.B. ein approximatives oder probabilistisches, immer noch das bessere ist.

Mit dem Beweis von $P\neq NP$ wären NP-Probleme endgültig als schwer lösbar klassifiziert. $P\neq NP$ entspricht derzeit der Annahme der meisten Wissenschaftler, und der Beweis wäre weniger folgenschwer als der Beweis von P=NP .

In der Kryptologie ist Komplexität im Gegensatz zu den meisten anderen Bereichen eine erwünschte Eigenschaft. Die Sicherheit einiger asymmetrischer Verschlüsselungsverfahren basiert allein auf diesem Faktor. Ein NP-Algorithmus kann ein beliebiges asymmetrisches Kryptosystem brechen, indem er den geheimen Schlüssel „errät“ und mit dem Verfahren, das der eigentliche Empfänger der Nachricht benutzen würde, dieses effizient entschlüsselt und so den Schlüssel verifiziert. Ein Beweis von P=NP würde also bedeuten, dass die Aussicht besteht, diese Kryptosysteme in der Praxis zu brechen. Entsprechend steht die Lösung des P-NP-Problems in Zusammenhang mit der offenen Frage ob es Einwegfunktionen gibt. Falls es sie gibt, würde $P\neq NP$ folgen.

Basierend auf einem Artikel in:

Wikipedia.de