Joule-Thomson-Effekt
Der Joule-Thomson-Effekt (nicht zu verwechseln mit dem Thomson-Effekt) bezeichnet die Temperaturänderung eines Gases bei einer isenthalpen Druckminderung. Die Richtung und Stärke des Effekts wird durch die Stärke der anziehenden und abstoßenden Kräfte zwischen den Gasmolekülen bestimmt. Unter Normalbedingungen gilt für die meisten Gase und Gasgemische, z.B. für Luft, dass die Temperatur bei der Entspannung sinkt. Dagegen steigt sie z.B. bei Wasserstoff, Helium, Neon. In einem idealen Gas gibt es keine molekularen Kräfte, infolgedessen zeigt es keinen Joule-Thomson-Effekt. Der Joule-Thomson-Effekt spielt eine wichtige Rolle in der Thermodynamik von Gasen.
Beispiele von Auftreten und Anwendungen:
- Abkühlung von Sodawasser, Schlagsahne und Softeis beim Ausschäumen aus einer Druckflasche
- Gefrieren von Wasser in Beschneiungsanlagen, sogenannten Schneekanonen. Insbesondere bei Druckluftkanonen und Schneelanzen.
- Herstellung von Trockeneis beim Zahnarzt oder beim Trockeneisstrahlen
- Gasverflüssigung im Linde-Verfahren

Geschichte
Im Zusammenhang mit der Entdeckung des Ersten und Zweiten Hauptsatzes der Thermodynamik um die Mitte des 19. Jahrhunderts wurde die Bilanz von Arbeit und Wärme bei der Kompression und Entspannung von Luft mit steigender Messgenauigkeit untersucht. Zuvor war im Gay-Lussac-Versuch keine Temperaturänderung festgestellt worden, wenn Luft sich ohne Wärmefluss und Arbeitsleistung bei sinkendem Druck in ein größeres Volumen ausdehnt. Demnach hängt ihre Innere Energie nicht vom Volumen ab. Mit besserer Genauigkeit wurde dies im Jahre 1852 von James Prescott Joule und Sir William Thomson (dem späteren Lord Kelvin) überprüft, indem strömende Luft einer kontrollierten Druckminderung unterworfen wurde. Dazu wurde die Luft kontinuierlich durch ein dickes, langes, thermisch isoliertes Rohr, mit einer kleinen Blende auf halber Strecke, gepumpt und zeigte am anderen Ende eine kleine Abkühlung. Nach ihrer Publikation wird diese Temperaturänderung als Joule-Thomson-Effekt bezeichnet. Da die Zustandsgleichung des idealen Gases Konstanz der Temperatur ergeben würde, war damit auch festgestellt, dass Luft nicht exakt ein ideales Gas ist. Die 1873 vorgestellte van der Waals’sche Zustandsgleichung passt besser und ergibt eine schwache Volumenabhängigkeit der inneren Energie. Der Joule-Thomson-Effekt wurde 1895 von Carl von Linde zur Grundlage der technischen Luftverflüssigung und Gewinnung von reinem Sauerstoff und Stickstoff gemacht.
Die isenthalpe Entspannung

Im idealen Modell der isenthalpen Entspannung strömt ein thermisch isoliertes Gas aufgrund einer Druckdifferenz durch ein Hindernis, an dem es keine Arbeit leistet.
Es handelt sich um einen kontinuierlichen, irreversiblen Prozess, bei dem keine Wärme ausgetauscht wird. Der Ruhedruck oder Totaldruck, d.h. die Summe aus dem
statischen Druck und dem in der Strömungsgeschwindigkeit steckenden dynamischen Druck, der durch Aufstau zurückgewonnen wird, ist nach dem Hindernis aufgrund
der Irreversibilität des Prozesses geringer als vor der Drosselung. (Ein Totaldruckverlust tritt bei jeder reibungsbehafteten Strömung durch eine Blende aufgrund
von Verwirbelungen auf, oder auch bei einer reibungsfreien Überschallströmung mit einem Verdichtungsstoß über diesen Stoß.) Hat eine Gasmenge vor dem Hindernis
das Volumen
,
muss ihr die Volumenarbeit
zugeführt werden, um sie durch das Hindernis zu drücken, und sie gibt hinter dem Hindernis, wo sie das größere Volumen
einnimmt, die Arbeit
ab. Nach dem 1. Hauptsatz ändert sich ihre innere Energie dabei von
auf
Folglich ist die Enthalpie
konstant;
und
sind die Ruhedrücke jeweils vor und nach dem Hindernis.
Wenn wie beim idealen Gas die Enthalpie nur von der Temperatur und nicht vom Volumen abhängt (für 1 Mol:
),
bleibt bei der isenthalpen Entspannung auch die Temperatur gleich. Für reale Gase ist aber weder die innere Energie noch das Produkt pV unabhängig vom Volumen.
Das lässt sich mit dem kontinuierlich ablaufenden Versuch von Joule und Thomson genau beobachten, denn alle möglichen Störeffekte wie Wärmeüberträge oder
verschiedene kinetische Energien im Gasstrom sind gut beherrschbar. Das ist ein Vorteil gegenüber dem Gay-Lussac-Versuch, bei dem ein komprimiertes Gases sich einmalig in ein größeres Volumen entspannt. Dabei macht anfangs nur das
Gas nahe dem geöffneten Durchlass eine freie Expansion ins Vakuum, während das Gas in mittleren Bereichen des Behälters erst zum Durchlass hin beschleunigt
werden muss, was vom Gas im hinteren Bereich durch eine adiabatische Expansion und Abkühlung bewirkt wird. Die gesamte innere Energie bleibt dabei zwar konstant,
verteilt sich nun aber ungleichmäßig in der Gasmenge. Erst nach dem Ausgleich aller Unterschiede herrscht wieder einheitliche Temperatur, an der man eventuelle
Abweichungen vom idealen Gas ablesen kann.
Thermodynamik
Joule-Thomson-Koeffizient
Die Stärke und Richtung der Temperaturänderung wird durch den Joule-Thomson-Koeffizienten μ beschrieben:
Er stellt die partielle Ableitung der Temperatur T nach dem Druck p bei konstanter
Enthalpie H dar. Der Index H besagt, dass bei der Druckänderung die Enthalpie konstant zu halten ist. Ein positiver Wert
zeigt, dass die Temperatur bei der Druckminderung sinkt, ein negativer, dass sie steigt.
Die Ursache des Joule-Thomson-Effekts liegt in der Wechselwirkung der Gasteilchen. Da sich die Teilchen bei größerem Abstand anziehen (siehe Van-der-Waals-Kräfte), muss bei der Vergrößerung des Teilchenabstandes Arbeit geleistet werden. Die Teilchen werden langsamer, das Gas kühlt ab. Bei geringem Abstand stoßen sich die Teilchen aber ab, wodurch sie beschleunigt werden, wenn sie sich voneinander weg bewegen können, und das Gas erwärmt sich. Das Verhältnis der beiden Effekte hängt von der Temperatur und vom Druck ab. Der überwiegend wirksame Effekt bestimmt das Vorzeichen des Joule-Thomson-Koeffizienten. Beispielsweise beträgt die Abkühlung bei Stickstoff von Normaltemperatur und nicht zu hohem Druck pro 1 bar Druckminderung 0,14 K.
Um den Joule-Thomson-Effekt für die Abkühlung des Gases nutzen zu können, muss es in einem Zustand mit
sein. Diese Zustände liegen alle unter einer bestimmten Temperatur, die als Inversionstemperatur
Tinv bezeichnet wird, und unter einem bestimmten maximalen Druck (siehe Abbildung). Für Stickstoff beispielsweise sind die entsprechenden
Werte Tinv=607 K (334 °C) und p=40 MPa (400 bar). Will man im Linde-Verfahren hingegen Gase wie Wasserstoff, Helium oder Neon abkühlen, muss man die Gase vorkühlen, da ihre Inversionstemperaturen
bei 202 K, 40 K und 228 K liegen.
Im Modell des idealen Gases werden außer harten, elastischen Stößen keine Wechselwirkungen zwischen den Teilchen berücksichtigt. Ideale Gase weisen daher keinen Joule-Thomson-Effekt auf.
Berechnung des Joule-Thomson-Koeffizienten
Wird die durch
definierte Enthalpie als Funktion ihrer natürlichen Variablen
Entropie
ausgedrückt, dann ist ihr totales Differential gegeben durch
Um den Joule-Thomson-Koeffizienten berechnen zu können, muss noch die Entropie durch die Variablen
ausgedrückt werden. Das Differential
lautet dann:
Damit kann man die Enthalpieänderung durch die Variablen Druck und Temperatur ausdrücken:
Nun ist im ersten Summanden
die Wärmekapazität bei konstantem Druck (denn
mit
und
da
).
Im zweiten Summanden gilt (nach der Maxwellrelation für die
freie Enthalpie mit dem totalen Differential
):
Dies ist durch den thermischen Ausdehnungskoeffizienten (bei konstantem Druck)
gegeben:
Einsetzen in die Gleichung für das Differential der Enthalpie liefert:
Durch Nullsetzen der linken Seite und Auflösen nach
erhält man den Joule-Thomson-Koeffizienten:
Für ein ideales Gas ist
,
und somit
:
der Joule-Thomson-Effekt ist nicht vorhanden, im Einklang damit, dass die innere Energie des idealen Gases nicht vom Volumen abhängt. Bei
realen Gasen ist der Effekt hingegen auch in den Bereichen nicht zu hoher Drücke und Temperaturen
vorhanden, wo sie sich sonst in sehr guter Näherung ideal verhalten (wie etwa Stickstoff oder Luft unter Normalbedingungen).
Joule-Thomson-Koeffizient für ein Van-der-Waals-Gas
In einer genäherten Betrachtung wird die Van-der-Waals-Gleichung (für 1 Mol)
für zu
vereinfacht. Auflösen nach V ergibt
Aus einer Entwicklung in
sowie konsistent in
folgt
Daraus ergibt sich der Wärmeausdehnungskoeffizient
(
und
als konstant angenommen)
Für den Joule-Thomson-Koeefizienten folgt:
Man erkennt, dass der Effekt von den anziehenden Kräften (van der Waals-Parameter
)
und den abstoßenden (van der Waals-Parameter
)
in entgegengesetzter Weise beeinflusst wird. Der Koeffizient ist positiv, wenn die Temperatur unter einem kritischen Wert
| Gas | Tkrit [K] | Tinv [K] | Tkrit/Tinv |
|---|---|---|---|
| Luft | 132,6 | ≈760 | ≈5,7 |
| Wasserstoff | 33,18 | ≈200 | ≈6 |
| Helium | 5,19 | ≈40 | ≈7,5 |
liegt, und variiert mit der Temperaturabhängigkeit gemäß
.
Beides gibt die Beobachtungen gut wieder und stützt die gegebene physikalische Interpretation in qualitativer Weise. Verglichen mit der
kritischen Temperatur Tcrit= 8a/(27Rb) ist
die Inversionstemperatur 6,75fach höher, nämlich
.
Doch die Übereinstimmung dieser einfachen Formel mit den bei verschiedenen Gasen beobachteten Inversionstemperaturen ist nicht gut, und es fehlt auch
die beobachtete Abhängigkeit der Inversionstemperatur vom Druck. Für genauere Werte und eine Wiedergabe der ganzen Inversionskurve
muss die Näherung der Van-der-Waals-Gleichung um ein Glied ergänzt werden:
Dann wird der Wärmeausdehnungskoeffizient
und der Joule-Thomson-Koeffizient
Diese Gleichung ergibt für Stickstoff bei Zimmertemperatur und
Pa (100 bar) einen Wert von
, nahe am gemessenen Wert.
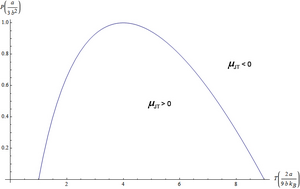
Die Inversionskurve im p-T-Diagramm erhält man, indem in der letzten Gleichung
gesetzt wird:
Umgestellt nach
,
ergibt sich für
eine nach unten offene Parabel. Physikalisch sinnvolle Werte
gehören zum Temperaturbereich
.
Diese Grenze ist der oben gefundene Wert der Inversionstemperatur, der also nur im Bereich niedriger Anfangsdrücke gilt. Will man zwecks stärkerer Abkühlung
bei höheren Anfangsdrücken arbeiten, muss die Temperatur tiefer liegen, wobei der maximal mögliche Druck
die Temperatur
erfordert.
Technische Aspekte
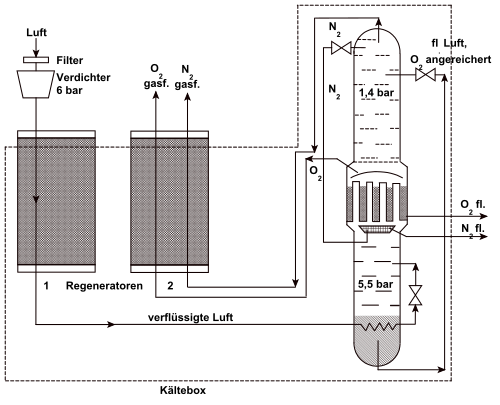
Das Linde-Verfahren zur Gasverflüssigung setzt einen positiven Joule-Thomson-Koeffizienten voraus. Nur so kann die Energie des komprimierten Gases abgeführt werden, obwohl die Umgebungstemperatur höher ist als die des Gases. In der Linde-Maschine wird Luft durch ein Drosselventil von etwa 200 bar auf etwa 20 bar entspannt. Dabei kühlt sie sich um etwa 45 Kelvin ab. Die abgekühlte Luft wird nun genutzt, um weitere komprimierte Luft vor der Entspannung abzukühlen (Gegenstrom-Wärmeübertrager). Über mehrere Kompressions- und Entspannungsstufen kann somit das Gas so weit abgekühlt werden, dass es kondensiert und somit flüssig wird.
Ein Gas, das bei Raumtemperatur einen negativen Joule-Thomson-Koeffizient aufweist, muss, damit das Linde-Verfahren wirken kann, mit anderen Verfahren vorgekühlt werden, bis seine Inversionstemperatur unterschritten ist. Erst dann kühlt es bei isenthalper Drosselung wegen des nun positiven Joule-Thomson-Koeffizienten weiter ab. So muss Helium auf ungefähr −243 °C (30 K) abgekühlt werden.
Literatur
- Peter W. Atkins: Physikalische Chemie. Wiley-VCH, Weinheim 2001, ISBN 3-527-30236-0.
- Refah Ayber: Thomson-Joule-Effekt von Methan-Wasserstoff- und Äthylen-Wasserstoff-Gemischen (VDI-Forschungsheft; Bd. 511). VDI-Verlag, Düsseldorf 1965.
- Lew Dawidowitsch Landau und Jewgeni Michailowitsch Lifschitz: Lehrbuch der Theoretischen Physik. Akademie-Verlag, Berlin
- 5. Statistische Physik. 1987, ISBN 3-05-500069-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.08. 2023