Gay-Lussac-Versuch
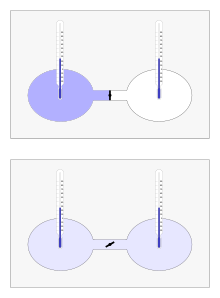
Der Gay-Lussac-Versuch (oder Joule-Versuch) ist ein klassisches Experiment der Wärmelehre. Es besteht in der freien Ausdehnung eines Gases in ein vorher evakuiertes Volumen, wobei weder Arbeit noch Wärme mit der Umgebung ausgetauscht werden können. Im kontrollierten Experiment strömt ein Gas nach dem Öffnen eines Ventils aus einem Behälter in einen zweiten Behälter über, bis der Druck ausgeglichen ist. So wurde es erstmals 1807 von Joseph Louis Gay-Lussac mit trockener Luft durchgeführt und heißt deshalb auch Gay-Lussacscher Überströmversuch. 1845 wurde es von James Prescott Joule mit größerer Genauigkeit wiederholt. Das Ergebnis war beide Male, dass die Temperatur insgesamt gleich blieb. Das wird heute dadurch erklärt, dass die Luft sich hier mit hinreichender Genauigkeit wie ein Ideales Gas verhält, dessen Innere Energie durch die Versuchsdurchführung konstant gehalten wird. Bei einem idealen Gas hängt die Temperatur bei gegebener Stoffmenge nur von der inneren Energie ab und ist insbesondere unabhängig vom eingenommenen Volumen. Bei genauerer Durchführung des Versuchs hätte sich jedoch eine Abkühlung zeigen müssen, denn genau genommen ist Luft kein ideales Gas. Der Gay-Lussac-Versuch darf nicht mit dem Joule-Thomson-Effekt oder dem Gesetz von Gay-Lussac verwechselt werden, die ebenfalls die Ausdehnung von Gasen zum Thema haben.
Geschichte
Zu Beginn des 19. Jahrhunderts wurde Wärme noch vorwiegend als ein feinstoffliches Fluidum verstanden, das die Temperatur einer Stoffmenge dadurch bestimmt, mit welcher Konzentration es darin vorhanden ist. Demzufolge hatte Gay-Lussac die Erwartung, die Temperatur müsse sinken, weil sich bei dem Expansionsversuch das Wärmefluidum verdünnt. Das traf für diejenige Hälfte der Luftmenge auch zu, die in dem vorher gefüllten Behälter nach dem Druckausgleich verblieben war, jedoch war die andere Hälfte, die in den gleich großen vorher evakuierten Behälter geströmt war, um den gleichen Betrag erwärmt, so dass insgesamt keine Abkühlung eintrat. Als zur Mitte des 19. Jahrhunderts hin zunehmend Erfahrungen mit der Erzeugung von Wärme durch mechanische Arbeit und umgekehrt vorlagen, wurden die Zweifel an der Auffassung der Wärme als Fluidum größer. Der Gay-Lussac-Versuch wurde daher 1845 von James Prescott Joule mit gesteigerter Sorgfalt und Messgenauigkeit wiederholt, wobei die beiden Gasbehälter sich in einem thermisch isolierten Wasserbad befanden. Es bestätigte sich, dass sich nach Ausgleich der anfänglichen Temperaturunterschiede die gleiche Temperatur einstellte wie vor der Expansion. Die Unabhängigkeit der inneren Energie vom Volumen war somit bestätigt und wurde – nach dem Gesetz von Boyle und Mariotte – zur zweiten definierenden Eigenschaft des idealen Gases.
Physikalische Beschreibung
Die Innere
Energie
einer gegebenen Stoffmenge ändert sich nach dem 1.
Hauptsatz der Thermodynamik um die Wärme
und die Arbeit
,
die aus der Umgebung zugeführt (oder, wenn sie negativ sind, abgeführt) werden:
ist eine Zustandsgröße
und damit eindeutig durch eine Funktion
gegeben, wobei
und
die Zustandsgrößen Volumen und Temperatur sind. Eine differentielle Änderung
hängt mit Änderungen von
und
so zusammen:
- Dabei ist
die isochore Wärmekapazität und
der Binnendruck.
Ist für einen Prozess ,
dann folgt für die Änderungen von
und
die Gleichung:
Die Expansion im Gay-Lussac-Versuch ist wegen
ein solcher Prozess mit
.
Dass dabei die Temperatur konstant bleibt, bedeutet
.
Folglich ist hier
.
Die innere Energie des idealen Gases hängt bei gegebener Temperatur nicht vom Volumen ab.
Nach dem 2.
Hauptsatz der Thermodynamik kann man diese Eigenschaft des idealen Gases
schon aus seiner thermischen Zustandsgleichung ()
heraus begründen. Aus der Existenz der Zustandsgröße Entropie
ist nach den Maxwell-Relationen
nämlich herzuleiten:
.
Da wegen der thermischen Zustandsgleichung des idealen Gases gilt, dass
,
ergibt sich als zwingende Folgerung .
Das ideale Gas ist demnach schon durch die thermische Zustandsgleichung
hinreichend definiert, denn die Bedingung, dass die innere Energie vom Volumen
unabhängig sei, ist darin schon enthalten.
Reales Gas
Dass Luft genau genommen kein ideales Gas ist, wurde von Joule und Kelvin wenige Jahre nach Joules Bestätigung des Gay-Lussac-Versuchs durch den Joule-Thomson-Effekt bewiesen. Demnach hätte sich bei genauer Messung auch bei den geschilderten Versuchen von Gay-Lussac und Joule schon eine Abkühlung zeigen müssen. Mithilfe der Van-der-Waals-Gleichung, einer thermischen Zustandsgleichung, die den realen Gasen besser entspricht als die oben benutzte Gleichung des idealen Gases, ergibt sich für die innere Energie der Ausdruck
, oder
Darin ist
die Wärmekapazität
der Gasmenge bei konstantem Volumen und
die Van-der-Waals-Konstante (die immer positiv ist) für die anziehenden Kräfte
zwischen den Gasteilchen. Hier hängt die innere Energie also explizit vom
Volumen ab.
Bei konstantem
folgt für die Messgröße des Experiments
.
Eine Expansion
zieht demnach stets eine Abkühlung nach sich:
.
Diese explizite Abhängigkeit der Temperatur vom Volumen lässt für die Versuche
von Joule (Anfangsdruck 22 bar bei Raumtemperatur, Verdopplung des Volumens)
eine Abkühlung der Luft um ca. 3,5 °C erwarten. Sie wurde damals übersehen, wohl
weil das umgebende Wasserbad eine viel größere Wärmekapazität besaß, sodass die
Endtemperatur sich nicht mehr messbar von der Anfangstemperatur unterschied.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.08. 2020