Schwarzschild-Metrik
| statisch |
rotierend | |
| ungeladen |
Schwarzschild-Metrik | Kerr-Metrik |
| geladen |
Reissner-Nordström-Metrik | Kerr-Newman-Metrik |
| Q: elektrische Ladung, J: Drehimpuls | ||
Die Schwarzschild-Metrik (auch: Schwarzschild-Lösung) bezeichnet, speziell im Rahmen der allgemeinen Relativitätstheorie, eine Lösung der Einsteinschen Feldgleichungen, die das Gravitationsfeld einer homogenen, nicht geladenen und nicht rotierenden Kugel beschreibt.
Die äußere Schwarzschild-Lösung ist die Vakuumlösung der Feldgleichungen für den sphärisch-symmetrischen Fall. Sie wurde 1916 von dem deutschen Astronomen und Physiker Karl Schwarzschild gefunden (und unabhängig von Johannes Droste) und war die erste bekannte exakte Lösung der einsteinschen Feldgleichungen.
Eine zweite, die innere Schwarzschild-Lösung, beschreibt die Metrik
einer homogen gedachten Flüssigkeitskugel. Die Integration der Feldgleichungen
reduziert sich auf die einfache lineare Summation eines Potentials (von
bis
für einen Körper mit Radius
oder ein als kugelförmig gleichverteilt gedachter Materie im Universum bis zu
seiner Grenze
).
Für die Zusammengehörigkeit beider Lösungen ist Voraussetzung, dass an der
Grenzfläche die Metrik
und ihre ersten Ableitungen übereinstimmen.
Das vollständige Schwarzschild-Modell besteht aus der inneren und der äußeren Lösung und beschreibt als einfachste Näherungslösung diverse astronomische Objekte wie Dunkelwolken oder Neutronensterne, lässt aber keine Spekulationen über Singularitäten wie Schwarze Löcher zu.
Äußere Lösung
Linienelement
Die einsteinschen Feldgleichungen
koppeln den Energie-Impuls-Tensor
über die einsteinsche Gravitationskonstante
mit der Geometrie des Raumes beschrieben durch den metrischen Tensor
.
Hierbei sind
der Ricci-Tensor
und
der Krümmungsskalar.
Im Vakuum mit
und unter der Annahme sphärischer Symmetrie lassen sich die Feldgleichungen
elementar integrieren. Für das Linienelement in Kugelkoordinaten
ergibt sich
.
Im häufig verwendeten natürlichen
Einheitensystem wird
gesetzt, so dass das Linienelement
lautet. Durch die Ersetzung von
durch
,
mit
als Gravitationskonstante und
durch
,
schließt man wieder an das physikalische Maßsystem an. Die Ausdrücke vor den Koordinatendifferenzialen
sind die Komponenten des zweistufigen metrischen
Tensors
in Schwarzschild-Koordinaten.
entspricht bis auf konstante Faktoren der gravitierenden Zentralmasse.
Geometrische Deutung
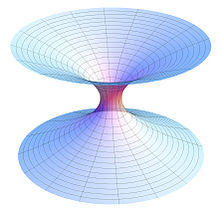
Das Linienelement kann auf zwei Arten interpretiert werden:
1. Deutet man die radiale Koordinatenlinie
als real begehbaren Weg, so stellt der im Linienelement enthaltene metrische
Tensor ein Spin-2-Feld dar. Dass dieses Feld
Gleichungen gehorcht, die sich aus der Riemannschen
Geometrie herleiten lassen, wird in diesem Fall nur als beiläufig
erachtet.
Man nennt
den Schwarzschild-Radius
und die dort befindliche Grenzfläche den Ereignishorizont,
wobei letzterer Begriff auch häufig als Synonym
für den Schwarzschild-Radius verwendet wird. An dieser Stelle besitzt der
radiale Teil der Metrik eine Koordinatensingularität,
ein Artefakt der Schwarzschild-Koordinaten. Durch Wahl geeigneter Koordinaten,
wie der Kruskal-Szekeres-Koordinaten,
kann dieses Problem beseitigt werden. Innerhalb des Schwarzschild-Radius
vertauschen Raum- und Zeitkoordinate ihre Bedeutung, da das radiale
Linienelement zeitartig und das vormals zeitartige Linienelement
raumartig wird.
Eine Bewegung durch den Raum wird eine Bewegung durch die Zeit und
umgekehrt.
Ein Ereignishorizont existiert erst, wenn sich eine große Masse, wie etwa der
Kern eines schweren Sterns, auf einen Bereich innerhalb ihres
Schwarzschild-Radius zusammengezogen hat – Masse außerhalb eines Radius von
ist irrelevant. Solch ein Objekt wird als Schwarzes
Loch bezeichnet, wobei dieses bei
nun eine physikalische Singularität enthält.
Die Kruskal-Szekeres-Koordinaten enthalten Lösungen für eine mögliche Verknüpfung zu einem weißen Loch, aus welchem Materie aus- aber nicht eindringen kann. Verbindungen dieser Art heißen Wurmlöcher und der Übergang von einem schwarzen- zu einem weißen Loch die Einstein-Rosen-Brücke. Das Schwarzschild-Wurmloch ist zwar eine mathematische Lösung der Einsteingleichungen, kann jedoch nicht existieren, da die Verbindung zu keinem Zeitpunkt geschaffen wird. Selbst im Falle einer offenen Verbindung kollabiert diese bei Annäherung an die Singularität. Stabil wäre sie nur unter Verwendung einer spekulativen, negativen Energiedichte.
2. Die andere Interpretation lehnt sich an die ursprüngliche Konzeption
Einsteins an, Gravitation
als Krümmung der Raumzeit zu verstehen. Die Krümmungen der Raumzeit bestimmen
dabei die Gravitationswirkungen. Aus Gründen der besseren Verständlichkeit kann
man sich die Raumzeit in einen höherdimensionalen Raum eingebettet vorstellen,
um dann ihre Krümmung zu veranschaulichen. Für den Raumteil des
Schwarzschild-Modells lässt sich die dahinterliegende Geometrie recht einfach
offenlegen. Das radiale Linienelement ist ein Element auf der (liegenden) Parabel
wobei R die zusätzliche Dimension im Einbettungsraum bezeichnet, die
Extradimension genannt wird. An
liegt die Leitlinie der Parabel und an
ihr Scheitel. Rotiert man den oberen Ast der Parabel
um die Leitlinie durch den Winkel
erhält man unter Hinweglassung der letzten zwei Dimensionen eine Fläche
4. Ordnung, das Flammsche Paraboloid.
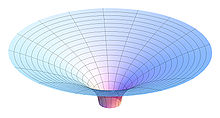
Die Koordinate
ist im Rahmen dieser Betrachtung kein begehbarer Weg, sondern eine
Hilfsvariable. Innerhalb des Schwarzschild-Radius kann dieses Modell keine
Aussagen machen, die Variable
hat den Wertebereich
Das am Flammschen Paraboloid entstehende 'Loch' innerhalb
wenn es sich eben nicht um ein Schwarzes Loch handelt, wird mit einer weiteren
Fläche überdeckt, die aus der inneren Schwarzschildschen Lösung hergeleitet
werden kann.
Die Extradimension
wird aus Gründen der Nützlichkeit eingeführt und dient zur Veranschaulichung der
geometrischen Verhältnisse. Ihr braucht keine physikalische Realität zugeordnet
werden. Gekrümmte Räume können durch ihre inneren Eigenschaften ohne
Zuhilfenahme eines Einbettungsraums beschrieben werden und unser
Anschauungsvermögen lässt auch nicht mehr als vier Dimensionen zu.
Anwendungen
Obwohl die äußere Schwarzschild-Metrik nur näherungsweise das Feld eines stellaren Objekts beschreibt, so führt sie auf unser Sonnensystem angewendet zu befriedigenden Ergebnissen. Die mit ihrer Hilfe berechneten Werte für die Ablenkung des Lichtes an der Sonne und der Periheldrehung der inneren Planeten stimmen mit den Beobachtungen gut überein. Für die Physik innerhalb und außerhalb von Sternen verwendet man jedoch das vollständige Schwarzschild-Modell mit der inneren Schwarzschild-Lösung für den Bereich innerhalb des Sterns.
Innere Lösung
Linienelement
Unter den obigen Bedingungen ist das Linienelement in Kugelkoordinaten
eine strenge Lösung der Einstein'schen
Feldgleichungen.
ist eine Konstante und
der Wert der radialen Variable an der Grenzfläche der inneren Lösung und der
äußeren Lösung, somit der Wert an der Oberfläche des stellaren Objekts.
Geometrische Deutung
Die von Einstein in die Gravitationsphysik eingeführten geometrischen Methoden legen es nahe, auch das obige Linienelement geometrisch zu deuten. Durch die Substitution
erhält man
woraus ersichtlich ist, dass der Raumteil der Metrik das Linienelement auf
einer dreidimensionalen Kugelhaube
im vierdimensionalen ebenen Raum mit dem Radius
und mit dem Öffnungswinkel
ist.
Vollständige Schwarzschild-Lösung
Um zu einer Vorstellung zu kommen, wie sich die vollständige
Schwarzschildsche Lösung mit Hilfe einer Extradimension in einem ebenen Raum
einbetten lässt, beschränkt man sich zunächst auf die ersten zwei Terme der
Linienelemente. Die äußere Lösung wird durch das Flammsche Paraboloid
visualisiert. Diese Fläche wird an geeigneter Stelle
abgeschnitten und von unten her eine Kugelhaube so angepasst, dass die
Tangentialflächen beider Schwarzschild-Flächen zusammenfallen.
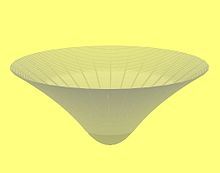
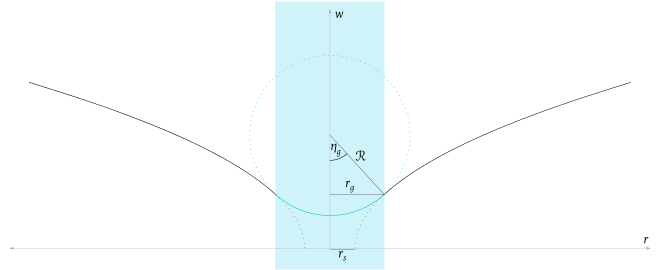
Hinzunahme des dritten Terms in der Metrik bringt eine Wiederholung dieser
Überlegung für eine weitere Teilfläche. Der Zeitteil der Metrik ist nur dann
verständlich, wenn man den darin enthaltenen Faktor 3 auf eine Grundeigenschaft
der Parabel als bestimmende Kurve der äußeren Lösung zurückführt. Verlängert man
den Krümmungsvektor
der Parabel bis zu ihrer Leitlinie, so haben die Abschnitte der entstehenden
Strecke das Verhältnis 1:2. Da an der Grenzfläche der Abstand der Parabel zur
Leitlinie
ist, hat der Krümmungsvektor dort die Länge
und die ganze Strecke
.
Die Projektion in die Richtung der Extradimension ist
.
Der Radiusvektor
zu einem beliebigen Punkt auf der Kugelhaube hat die Projektion
.
Die beiden Stecken werden um den imaginären Winkel
rotiert. Es entstehen zwei konzentrische imaginäre (offene) Kreise, deren
pseudoreelles Abbild Hyperbeln sind. (Imaginäre Kreise werden auch Hyperbeln
konstanter Krümmung genannt.) Der Abstand der Kreise entspricht dem
Klammerausdruck in der obigen Metrik. Beim Fortschreiten auf den Kreisen um
überstreicht diese Strecke eine Fläche, die proportional zur vergangenen Zeit
ist.
Erhaltungssatz
Den Energie-Impulstensor der Materie berechnet man aus den Feldgleichungen. Er hat die Form
.
mit der Gravitationskonstante
,
nimmt nach innen zu, was der Anziehung der Flüssigkeitskugel auf ihre äußeren
Teile entspricht. Ein Blick auf den Nenner der Druckfunktion zeigt, dass bei zu
großem Grenzwinkel
der Druck unendlich wird, bzw. das Vorzeichen
wechselt und nach außen gerichtet ist. Dadurch geht die Stabilität des
Himmelskörpers verloren. Andererseits hat die Druckfunktion eine so steile
Flanke, dass man durch die innere Schwarzschild-Lösung auch exotische Objekte
beschreiben kann, deren innerer Druck so hoch ist, dass die atomare oder sogar
die elementare Struktur der Materie zusammenbricht. Keinesfalls kann jedoch an
den Ereignishorizont
eine Halbkugel angepasst werden. Im Rahmen der vollständigen
Schwarzschild-Lösung können auch keine schwarzen Löcher
beschrieben werden.
Die Energiedichte
entspricht bis auf einen Faktor
der Materiedichte und ist konstant, was die Inkompressibilität der Flüssigkeit
zum Ausdruck bringt. Druck und Energiedichte sind kovariant erhalten. In
bedeutet der Doppelstrich die kovariante
Ableitung in der Vierbeindarstellung. Aus dem einfachen Aufbau von
erhält man
.
Die Druckzunahme nach innen ist durch die Schwerewirkung des Gravitationsfeldes
bestimmt. Druck und Energiedichte sind zeitlich konstant. Der Energie-Impulstensor ist geometrischer Natur. Die oben angeführten Ausdrücke für den Druck und die Energiedichte leiten sich aus den verallgemeinerten zweiten Fundamentalformen der Flächentheorie her, die Einstein'schen Feldgleichungen aus den Gaußschen Gleichungen und der Erhaltungssatz aus den Mainardi-Codazzi-Gleichungen. Die innere Schwarzschild-Lösung kann als erster und sehr einfacher Versuch der Geometrisierung der Materie angesehen werden.
Verallgemeinerungen zu anderen Metriken
Unter Hinzunahme zusätzlicher physikalischer Phänomene wie elektrischer Ladung, Drehimpuls oder Extradimensionen gibt es wohlbekannte exakte Lösungen der Einsteinschen Feldgleichungen. Dies sind im Einzelnen die Kerr-Metrik bei Hinzunahme von Drehimpuls, die eine Vakuumlösung rotierender, aber ungeladener schwarzer Löcher darstellen.
Betrachtet man hingegen weiterhin statische (verschwindender Drehimpuls), aber dafür elektrisch geladene schwarze Löcher, erhält man als exakte Lösung die Reissner-Nordström-Metrik. Die Kerr-Newman-Metrik ist eine exakte Lösung für sowohl rotierende als auch elektrisch geladene schwarze Löcher in vier Dimensionen.
Die einfachste exakte Lösung Schwarzschild-artiger schwarzer Löcher in
(räumlichen) Extradimensionen (sodass insgesamt
Dimensionen verwendet werden) ist die Schwarzschild-Tangherlini-Metrik.
Sie stellt ebenfalls die Lösung des elektrisch neutralen statischen Problems
dar.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.04. 2021