Gravitationskonstante

Physikalische Konstante
Name	Gravitationskonstante
Formelzeichen
Wert
SI	6.67430(15) · 10 ^-11 $\textstyle {\frac {\mathrm {m^{3}} }{\mathrm {kg\,s^{2}} }}$
Unsicherheit (rel.)	2.2·10^-5
Planck-Einheiten	1. Gelegentlich wird aber auch $8\pi \;G$ auf 1 gesetzt.
Quellen und Anmerkungen
Quelle SI-Wert: CODATA 2018

Die Gravitationskonstante (Formelzeichen oder $\gamma$ ) ist die fundamentale Naturkonstante, die die Stärke der Gravitation bestimmt. In dem Gravitationsgesetz nach Isaac Newton ergibt sie direkt die Stärke der Gravitationskraft zwischen zwei Körpern in Abhängigkeit von ihrem Abstand und ihren Massen, in der allgemeinen Relativitätstheorie nach Albert Einstein bestimmt sie die Krümmung der vierdimensionalen Raumzeit und damit den Ablauf aller mit der Gravitation zusammenhängenden Erscheinungen. Für die Beschreibung astronomischer Größen und Vorgänge besitzt sie fundamentale Bedeutung. Der Wert der Gravitationskonstanten beträgt

$G=(6{,}674\,30\pm 0{,}000\,15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} ,$

wobei bereits die vierte Dezimalstelle unsicher ist.

Definition

Nach dem newtonschen Gravitationsgesetz ziehen sich zwei kugelsymmetrische Körper mit den Massen $m_{1}$ und $m_{2}$ , deren Mittelpunkte einen Abstand haben, gegenseitig mit der Kraft

$F = G\, \frac{m_1 \, m_2}{r^2}$

an. Die in der Gleichung auftretende Proportionalitätskonstante ist die Gravitationskonstante.

Diese Form des Gesetzes wurde 1873, 200 Jahre nach Newton, durch Alfred Cornu und Jean-Baptistin Baille eingeführt. Newton schrieb sein Gesetz ohne Nennung der Konstante in Form der Proportionalitäten $F\propto m_{1}\ ,\ F\propto m_{2}\ ,\ F\propto r^{-2}$ , wie es damals in der wissenschaftlichen Literatur üblich war.

Wert und Einheiten

Im Internationalen Einheitensystem (SI) beträgt der Wert nach der aktuellen Empfehlung CODATA 2018:

$G=6{,}674\,30(15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}}$

(also mit einer geschätzten Standardunsicherheit von $0{,}000\,15\cdot 10^{-11}\,\mathrm {m} ^{3}/(\mathrm {kg} \cdot \mathrm {s} ^{2})$ ).

Im CGS-Einheitensystem hat den Wert

$G=6{,}674\,30(15)\cdot 10^{-8}\,\mathrm {\frac {cm^{3}}{g\cdot s^{2}}} .$

Die Gravitationskonstante kann auch mit anderen Naturkonstanten ausgedrückt werden, zum Beispiel mit Hilfe des reduzierten Planckschen Wirkungsquantums $\hbar$ und der Lichtgeschwindigkeit („natürliche Einheiten“). Nach CODATA 2018 ergibt sich als Wert:

$G=6{,}708\,83(15)\cdot 10^{-39}\,{\frac {\hbar c}{(\mathrm {GeV} /c^{2})^{2}}}$

Verglichen mit anderen Grundkräften der Physik ist die Gravitation eine sehr schwache Wechselwirkung, was sich in dem kleinen Wert der Gravitationskonstanten ausdrückt. Berechnet man beispielsweise den Betrag des Verhältnisses zwischen der Gravitationskraft und der elektrostatischen Kraft zwischen zwei Protonen, so erhält man unabhängig vom Abstand:

$\left|{\frac {F_{\text{Gravitation}}}{F_{\text{elektrisch}}}}\right|={\frac {Gm_{\text{Proton}}^{2}}{e^{2}/(4\pi \varepsilon _{0})}}\approx 10^{-36}$

Messungen

Die Gravitationskraft zwischen der Erde und einem anderen Objekt, d.h., sein Gewicht, lässt sich zwar sehr genau messen, allerdings müsste man, um daraus die Gravitationskonstante mit gleicher Genauigkeit zu bestimmen, die Erdmasse oder besser die ganze Massenverteilung in der Erde zuverlässig kennen. Das ist aber nicht gegeben, sodass zur Messung von die überaus geringe Anziehungskraft zwischen Körpern bekannter Masse im Labor bestimmt werden muss. Beispielsweise beträgt die Anziehungskraft zwischen zwei Körpern von je 100 kg Masse in 1 m Abstand weniger als 10⁻⁹ (ein Milliardstel) ihrer Gewichtskraft, und alle andere Materie im Labor oder außerhalb davon übt auf die Testkörper ebenfalls Gravitation aus. Diese Messungen gestalten sich daher schwierig. Schon kleinste Temperaturunterschiede, Luftströmungen, Ungleichmäßigkeiten im Material oder Kriechen des Materials, sogar die Anzahl der Fahrzeuge auf dem Parkplatz vor dem Institutsgebäude, verfälschen die Ergebnisse.

Aktueller Stand

Ein Wert für mit achtstelliger Genauigkeit, wie für andere Naturkonstanten längst erreicht, würde hier also eine Reduzierung solcher möglichen Störeinflüsse auf 10⁻¹⁷ (ein Hundertbilliardstel) der Gewichtskraft der beteiligten Körper erfordern. Das ist bisher nicht gelungen. Fünfstellige Genauigkeit ist somit die höchste, sie wurde für eine Messung von aus dem Jahr 2000 angegeben. Allerdings gibt es allein aus den letzten drei Jahrzehnten insgesamt 13 weitere Messergebnisse aus Labors rund um die Welt mit verschiedenen Apparaturen, die z.T. ähnlich hohe Genauigkeit angeben, sich aber dennoch bis fast zum Zehnfachen der jeweils angegebenen Unsicherheitsbereiche unterscheiden. Es wird vermutet, dass die einzelnen Apparaturen noch unerkannte Schwachstellen haben.

Im Ergebnis kann die relative Unsicherheit im Wert von derzeit nicht unter 2,2 · 10⁻⁵ gedrückt werden. Damit ist unter den grundlegenden Naturkonstanten zurzeit diejenige mit der geringsten Messgenauigkeit. Zum Vergleich: Die Rydberg-Konstante ist in SI-Einheiten mit einer relativen Unsicherheit von 1,9 · 10⁻¹² bekannt, das ist mehr als millionenfach genauer.

Die – im Vergleich – geringe Genauigkeit von und die zu große Streubreite der Einzelergebnisse gelten als Mängel. Die Streubreite könnte außer auf unerkannte Schwachstellen der Messapparaturen auch auf einen noch unverstandenen Aspekt der Gravitation hinweisen. Die Ungenauigkeit begrenzt die Möglichkeit, aus der Gravitation eines Himmelskörpers seine Masse bestimmen zu können. Dazu muss der Himmelskörper von einem Begleiter umrundet werden, dessen Bahnradius und Umlaufkreisfrequenz $\omega$ bekannt sind, sodass der Gravitationsparameter $\mu = r^3 \omega^2$ bestimmt werden kann. Das ist oft mit hoher Genauigkeit möglich, für die Erde z.B. mit bis zu 10-stelliger Genauigkeit (siehe WGS 84). Dann ergibt sich die Masse des Himmelskörpers aus $M=\mu /G$ (siehe Keplersche Gesetze). Das ist trotz der Unsicherheit in wesentlich genauer, als wenn man die Masse aus dem Durchmesser und dem Dichteverlauf im Innern des Himmelskörpers schätzte.

In neuesten Experimenten wird die Gravitationskonstante mit zwei unterschiedlichen Verfahren durch die Variation des Versuchsaufbaus der Pendelwaage gemessen:

Schwingungszeit-Methode: Ein vergoldeter Quarzblock an einer Glasfaser und zwei jeweils 778 Gramm schwere Stahlkugeln ändern die Torsionsschwingungen, mit dem Ergebnis der Gravitationskonstanten von $6{,}674\,184\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}}$ ±11,64 ppm.
Methode zur Messung der Winkelbeschleunigung: Im zweiten Versuchsaufbau können sich beide Massen (Quarzblock und Stahlkugeln) unabhängig drehen und der Drehtisch wird so nachgeführt, dass die Torsion kompensiert wird, wodurch kein Drehwinkel, sondern die Winkelbeschleunigung („angular-acceleration-feedback method“) zur Kompensation des Drehwinkels gemessen wird, woraus ein Wert von $6{,}674\,484\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}}$ ±11,61 ppm abgeleitet wurde.

In früheren Experimenten betrug die Standardabweichung ±47 ppm, sie wurde also um ±36 ppm verbessert.>

Das Cavendish-Experiment

Cavendish-Experiment (1798)

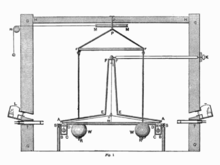
Die erste Messung der Gravitationskraft zwischen zwei Massen bekannter Größe gelang Henry Cavendish im Jahr 1798 mithilfe der eigens dafür erfundenen Gravitationswaage. Die Waage bestand aus zwei kugelförmigen Testmassen mit zusammen (in heutigen Einheiten) = 1,46 kg, die zu einer Hantel verbunden und an einem Torsionsdraht aufgehängt waren, sodass sie freie horizontale Drehschwingungen ausführen konnten. Zwei große Kugeln mit einer Gesamtmasse $M_{c}=316\,\mathrm {kg}$ , in gleichem Abstand r_m dicht neben je einer der Testmassen, erzeugten die Anziehungskraft, die die Testmassen ca. 1° aus der Ruhelage auslenkten. Aus dem Auslenkwinkel wurde die Torsionskraft F_c ermittelt, die der Anziehungskraft der großen und kleinen Kugeln bei diesem Abstand die Waage hält. Die dazu nötige Kenntnis der Torsionssteifigkeit des Drahtes wurde aus der Periodendauer der Torsionsschwingung gewonnen.

Aus Cavendishs Messwerten ergibt sich durch die Formel

${\frac {F_{c}\,r_{m}^{2}}{m\,M_{c}}}=G$

ein Wert für die Konstante

$G_{\mathrm {Cavendish} }=6{,}754\cdot 10^{-11}\,\mathrm {{m^{3}}\,{kg^{-1}\,s^{-2}}} .$

Dies verfehlt den heutigen Wert nur um 1,2 Prozent.

Allerdings war der Begriff einer Gravitationskonstante zu Cavendishs Zeiten noch gar nicht üblich, vielmehr wurde das Newtonsche Gravitationsgesetz ausschließlich in Form von Proportionalitäten gebraucht. Dementsprechend betrachtete er das Verhältnis der beiden Kräfte $F_{c}$ und F_E , mit denen die kleinen Kugeln von den großen bzw. von der Erde angezogen werden. Nach Newton gilt:

$\frac {F_c} {F_E} = \frac { M_c} {M_E}\ \frac {r_E^2} {r_m^2}$

F_E ist nichts anderes als das (Gesamt-)Gewicht der kleinen Kugeln, sodass die Erdmasse $M_{E}$ hierin die einzige Unbekannte ist. Cavendish konnte aus seinen Messdaten die Masse der Erde bestimmen. Populär wurde die physikalisch nicht korrekte und genau genommen sinnlose Formulierung, Cavendish habe „die Erde gewogen“.

Nachdem die Erdmasse, implizit also der Wert der Gravitationskonstante bekannt war, konnten auch die Massen weiterer Himmelskörper des Sonnensystems bestimmt werden.

Siehe auch

Gaußsche Gravitationskonstante

Basierend auf einem Artikel in:

Wikipedia.de