Pythagoreische Primzahl

In der Zahlentheorie ist eine pythagoreische Primzahl (vom englischen pythagorean prime) eine Primzahl $p\in \mathbb {N}$ der Form $p=4n+1$ mit $n\in \mathbb {N}$ (nicht zu verwechseln mit Pythagoraszahl). Ist eine Primzahl keine pythagoreische Primzahl, so heißt sie nicht-pythagoreische Primzahl.

Beispiele

Die kleinsten pythagoreischen Primzahlen sind die folgenden:

5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, 149, 157, 173, 181, 193, 197, 229, 233, 241, 257, 269, 277, 281, 293, 313, 317, 337, 349, 353, 373, 389, 397, 401, 409, 421, 433, 449, 457, 461, 509, 521, 541, 557, 569, 577, 593, 601, 613, 617, … (Folge A002144 in OEIS)

Eigenschaften

Jede pythagoreische Primzahl kann als Summe von zwei Quadraten dargestellt werden.

Beweis:

Der Beweis folgt direkt aus Fermatschem Satz über die Summe von zwei Quadraten. Gelegentlich nennt man diesen Satz auch Girard’s Theorem.

Beispiel:

$41=4^{2}+5^{2}$ , $101=1^{2}+10^{2}$ , …

Die Umkehrung der obigen Eigenschaft gilt ebenfalls:

Ist die Summe von zwei Quadraten eine ungerade Primzahl, so ist sie eine pythagoreische Primzahl.

Beweis:

Der Beweis folgt ebenfalls direkt aus Fermatschem Satz über die Summe von zwei Quadraten:

Für das Quadrat einer geraden Zahl $n:=2k$ mit $n,k\in \mathbb {Z}$ gilt: $n^{2}=(2k)^{2}=4k^{2}\equiv 0{\pmod {4}}$ .

Für das Quadrat einer ungeraden Zahl $m:=2k+1$ mit $m,k\in \mathbb {Z}$ gilt: $m^{2}=(2k+1)^{2}=4k^{2}+4k+1\equiv 1{\pmod {4}}$ .

Für ungerade Primzahlen $p\in \mathbb {P}$ gilt: $p\equiv 1{\pmod {4}}$ (für pythagoreische Primzahlen) oder $p\equiv 3{\pmod 4}$ (für nicht-pythagoreische Primzahlen).

Die Summe von zwei Quadratzahlen ist aus obigen Gründen immer $\equiv 0{\pmod {4}}$ , $\equiv 1{\pmod {4}}$ oder $\equiv 2{\pmod {4}}$ , aber niemals $\equiv 3{\pmod {4}}$ . Ist sie also eine ungerade Primzahl, so bleibt nur $\equiv 1{\pmod {4}}$ übrig und das sind genau die pythagoreischen Primzahlen. $\Box$

Für jede pythagoreische Primzahl $p\in \mathbb {P}$ gibt es ein rechtwinkliges Dreieck mit Hypotenusenlänge $\sqrt{p}$ , welches ganzzahlige Kathetenlängen hat.

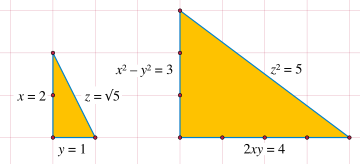
Die pythagoreische Primzahl

und seine Quadratwurzel als Hypotenusen von rechtwinkligen Dreiecken und wie man aus dem kleinen Dreieck das große berechnen kann

Beweis:

Siehe Satz des Pythagoras

Ist die Primzahl $p\in \mathbb {P}$ die Hypotenusenlänge eines rechtwinkligen Dreiecks, so ist eine pythagoreische Primzahl und größter Teil eines pythagoreischen Tripels.
Es gibt unendlich viele pythagoreische Primzahlen.

Beweis:

Siehe Dirichletscher Primzahlsatz

Das Primrennen zwischen 4n+1 und 4n+3

Sei $x\in \mathbb {N}$ . Dann gilt:

Die Anzahl der pythagoreischen Primzahlen (der Form $4n+1$ ) bis ist annähernd gleich wie die Anzahl der nicht-pythagoreischen Primzahlen (der Form $4n+3$ ) bis . Im Speziellen ist die Anzahl der pythagoreischen Primzahlen bis oft etwas kleiner. Dieses Phänomen nennt man auf Englisch Chebyshev's bias und stammt vom Mathematiker Pafnuti Lwowitsch Tschebyschow.

Beispiele

Bis $x=600000$ gibt es nur zwei Zahlen, unter denen mehr pythagoreische Primzahlen (der Form $4n+1$ ) als nicht-pythagoreische (ungerade) Primzahlen (der Form $4n+3$ ) existieren, nämlich $26861$ und $26862$ . Zwischen $26863$ und $26878$ sind es gleich viele und ab $26879$ gibt es wieder mehr nicht-pythagoreische (ungerade) Primzahlen.
Die folgende Liste zeigt an, wann ein „Führungswechsel“ im „Rennen“ pythagoreische Primzahlen gegen nicht-pythagoreische (ungerade) Primzahlen stattfindet (auf englisch Where prime race 4n-1 vs. 4n+1 changes leader):

3, 26861, 26879, 616841, 617039, 617269, 617471, 617521, 617587, 617689, 617723, 622813, 623387, 623401, 623851, 623933, 624031, 624097, 624191, 624241, 624259, 626929, 626963, 627353, 627391, 627449, 627511, 627733, 627919, 628013, 628427, 628937, 629371, … (Folge A007350 in OEIS)

Zusammenhang mit Gaußschen Primzahlen

Die Norm einer Gaußschen Zahl der Form $x+\mathrm {i} \cdot y$ ist $\|x+\mathrm {i} \cdot y\|=x^{2}+y^{2}$ . Es gilt:

Eine pythagoreische Primzahl (inklusive der Primzahl ) kann immer als Norm einer Gaußschen ganzen Zahl dargestellt werden. Ungerade nicht-pythagoreische Primzahlen können das nicht.
Eine pythagoreische Primzahl ist keine Primzahl in der Menge der Gaußschen Primzahlen. Der Realteil und der Imaginärteil ihrer Primfaktoren in dieser Faktorisierung sind die Kathetenlängen des rechtwinkligen Dreiecks mit gegebener Hypotenusenlänge .

Beweis:

Es kann jede pythagoreische Primzahl $p=x^{2}+y^{2}$ zerlegt werden in $p=x^{2}+y^{2}=(x+\mathrm {i} \cdot y)\cdot (x-\mathrm {i} \cdot y)$ .

Vergleiche dazu auch die Gruppe der rationalen Punkte auf dem Einheitskreis.

Quadratische Reste

Seien $p,q\in \mathbb {P}$ zwei verschiedene ungerade Primzahlen, wobei mindestens eine der beiden eine pythagoreische Primzahl sein soll. Dann gilt:

ist quadratischer Rest modulo genau dann, wenn quadratischer Rest modulo ist.

Mit anderen Worten:

Seien $p,q\in \mathbb {P}$ mit $p>2,q>2,p\not =q$ und $p\equiv 1{\pmod {4}}$ . Dann gilt mit dem Legendre-Symbol:

$\left({\frac {p}{q}}\right)=1\Longleftrightarrow \left({\frac {q}{p}}\right)=1$

Beispiel:

Sei $p=37\equiv 1{\pmod {4}}$ und $q=47\equiv 3{\pmod {4}}$ . Dann ist $15^{2}=225\equiv 37{\pmod {47}}$ und somit ist quadratischer Rest modulo . Umgekehrt ist $11^{2}=121\equiv 84\equiv 47\equiv 10{\pmod {37}}$ und somit ist quadratischer Rest modulo .

Seien $p,q\in \mathbb {P}$ zwei verschiedene ungerade Primzahlen, wobei beide nicht-pythagoreische Primzahlen sein sollen. Dann gilt:

ist quadratischer Rest modulo genau dann, wenn kein quadratischer Rest modulo ist.

Mit anderen Worten:

Seien $p,q\in \mathbb {P}$ mit $p>2,q>2,p\not =q$ und $p,q\equiv 3{\pmod {4}}$ . Dann gilt:

$\left({\frac {p}{q}}\right)=1\Longleftrightarrow \left({\frac {q}{p}}\right)=-1$

Beispiel:

Sei $p=47\equiv 3{\pmod {4}}$ und $q=43\equiv 3{\pmod {4}}$ . Dann ist $41^{2}=1681\equiv 47\equiv 4{\pmod {43}}$ und somit ist quadratischer Rest modulo . Umgekehrt gibt es aber kein mit $x^{2}\equiv 43{\pmod {47}}$ und somit ist kein quadratischer Rest modulo .

Siehe auch

Quadratisches Reziprozitätsgesetz

Basierend auf einem Artikel in:

Wikipedia.de