Empirische Verteilungsfunktion
Eine empirische Verteilungsfunktion – auch
Summenhäufigkeitsfunktion oder Verteilungsfunktion
der Stichprobe genannt – ist
in der beschreibenden
Statistik und der Stochastik
eine Funktion,
die jeder reellen Zahl
den Anteil der Stichprobenwerte, die kleiner oder gleich
sind, zuordnet. Die Definition der empirischen Verteilungsfunktion kann in
verschiedenen Schreibweisen erfolgen.
Definition
Allgemeine Definition
Wenn
die Beobachtungswerte in der Stichprobe sind, dann ist die empirische
Verteilungsfunktion definiert als
mit ,
wenn
und Null sonst, d.h.
bezeichnet hier die Indikatorfunktion
der Menge
.
Die empirische Verteilungsfunktion entspricht somit der Verteilungsfunktion der
empirischen
Verteilung.

Alternativ lässt sich die empirische Verteilungsfunktion mit den
Merkmalsausprägungen
und den zugehörigen relativen
Häufigkeiten
in der Stichprobe definieren:
Die Funktion
ist damit eine monoton
wachsende rechtsstetige
Treppenfunktion
mit Sprüngen an den jeweiligen Merkmalsausprägungen.
Definition für klassierte Daten
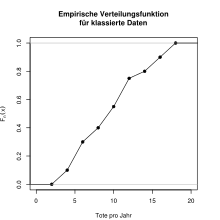
Manchmal liegen Daten nur klassiert
vor, d.h. es sind
Klassen mit Klassenuntergrenzen
,
Klassenobergrenzen
und relativen Klassenhäufigkeiten
gegeben,
.
Dann wird die Verteilungsfunktion definiert als
An den Klassenober- und -untergrenzen stimmt die Definition mit der Definition für unklassierte Daten überein, in den Bereichen dazwischen jedoch findet nun eine lineare Interpolation statt, bei der man unterstellt, dass die Beobachtungen innerhalb der Klassen gleichmäßig verteilt sind. Empirische Verteilungsfunktionen klassierter Daten sind damit (ebenso wie Verteilungsfunktionen stetiger Wahrscheinlichkeitsverteilungen, z.B. der Normalverteilung) zwar stetig, doch nur zwischen den Klassengrenzen differenzierbar, wobei ihr Anstieg der Höhe der jeweiligen Säule des zugrundeliegenden Histogramms entspricht.
Zu beachten ist dabei allerdings, dass die Intervallgrenzen klassierter Daten nach Möglichkeit so gewählt werden, dass die beobachteten Merkmalsausprägungen zwischen und nicht (wie im Fall unklassierter Daten) auf den Intervallgrenzen liegen, wodurch je nach Wahl der Klassengrenzen für ein und denselben Datenbestand ggf. leicht verschiedene Summenhäufigkeitspolygone entstehen können.
Beispiele
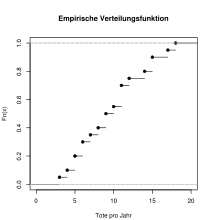
Allgemeiner Fall: Unklassierte Daten
Als Beispiel sollen die Pferdetrittdaten von Ladislaus von Bortkewitsch dienen. Im Zeitraum von 1875 bis 1894 starben in 14 Kavallerieregimentern der preußischen Armee insgesamt 196 Soldaten an Pferdetritten:
| Jahr | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | |
| Tote | 3 | 5 | 7 | 9 | 10 | 18 | 6 | 14 | 11 | 9 | 5 | 11 | 15 | 6 | 11 | 17 | 12 | 15 | 8 | 4 | 196 |
Schreibt man die Tabelle mit den Merkmalsausprägungen und relativen Häufigkeiten auf, dann ergibt sich
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 14 | 15 | 17 | 18 | |
| Jahre | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 2 | 1 | 1 |
| 0,05 | 0,05 | 0,10 | 0,10 | 0,05 | 0,05 | 0,10 | 0,05 | 0,15 | 0,05 | 0,05 | 0,10 | 0,05 | 0,05 | |
| 0,05 | 0,10 | 0,20 | 0,30 | 0,35 | 0,40 | 0,50 | 0,55 | 0,70 | 0,75 | 0,80 | 0,90 | 0,95 | 1,00 |
Die letzte Zeile enthält den Wert der Verteilungsfunktion an der
entsprechenden Stelle .
Beispielsweise an der Stelle
ergibt sich
.
Klassierte Daten
Klassiert man die Daten, so erhält man folgende Datentabelle. Die Grafik dazu findet man bei der Definition.
| ab |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| bis |
4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 0,10 | 0,20 | 0,10 | 0,15 | 0,20 | 0,05 | 0,10 | 0,10 | |
| 0,10 | 0,30 | 0,40 | 0,55 | 0,75 | 0,80 | 0,90 | 1,00 |
Die letzte Zeile enthält den Wert der Verteilungsfunktion an der
entsprechenden Stelle .
An der Stelle
ergibt sich
.
Konvergenzeigenschaften
Das starke
Gesetz der großen Zahlen sichert zu, dass der Schätzer
fast
sicher für jeden Wert
gegen die wahre Verteilungsfunktion
konvergiert:
,
d.h. der Schätzer
ist konsistent. Damit ist die punktweise Konvergenz der empirischen
Verteilungsfunktion gegen die wahre Verteilungsfunktion gegeben. Ein weiteres,
stärkeres Resultat, der Satz von
Glivenko-Cantelli sagt aus, dass dies sogar gleichmäßig geschieht:
.
Diese Eigenschaft ist die mathematische Begründung dafür, dass es überhaupt sinnvoll ist, Daten mit einer empirischen Verteilungsfunktion zu beschreiben.
Ogive
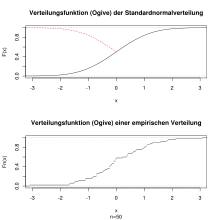
Ogive bezeichnete ursprünglich das gotische Bau-Stilelement Spitzbogen sowie die verstärkten Rippen in den Gewölben. Der Ausdruck wurde in der Statistik für eine Verteilungsfunktion erstmals 1875 von Francis Galton verwendet:
„When the objects are marshalled in the order of their magnitude along a level base at equal distances apart, a line drawn freely through the tops of the ordinates..will form a curve of double curvature... Such a curve is called, in the phraseology of architects, an ‘ogive’.“
Auf der horizontalen Achse des Koordinatensystems werden hier die geordneten (oft gruppierten) Merkmalsausprägungen aufgetragen; auf der vertikalen Achse die relativen kumulierten Häufigkeiten in Prozent.
Die Grafik rechts zeigt die kumulierte Verteilungsfunktion
einer theoretischen Standardnormalverteilung.
Wird der rechte Teil der Kurve an der Stelle
gespiegelt (rot gestrichelt), dann sieht die entstehenden Figur wie eine Ogive
aus.
Darunter wird eine empirische Verteilungsfunktion gezeigt. Für die Grafik wurden 50 Zufallszahlen aus einer Standardnormalverteilung gezogen. Je mehr Zufallszahlen man zieht desto stärker nähert man sich der theoretischen Verteilungsfunktion an.
Literatur
- Horst Mayer: Beschreibende Statistik. München – Wien 1995
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.04. 2023