Satz von Gliwenko-Cantelli

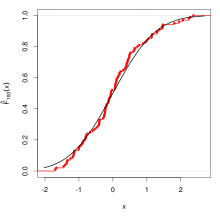
Empirische Verteilungsfunktion einer standardnormalverteilten Stichprobe vom Umfang n=100

Der Satz von Gliwenko-Cantelli oder Satz von Gliwenko, auch Hauptsatz der mathematischen Statistik oder Fundamentalsatz der Statistik genannt, englisch Central statistical theorem, ist ein mathematischer Lehrsatz auf dem Gebiet der Wahrscheinlichkeitsrechnung, welcher auf zwei Arbeiten der beiden Mathematiker Waleri Iwanowitsch Gliwenko und Francesco Cantelli aus dem Jahre 1933 zurückgeht. Aus dem Satz geht hervor, dass bei unabhängig durchgeführten Zufallsversuchen die aus den Zufallsstichproben gewonnenen empirischen Verteilungsfunktionen einer Zufallsgröße gleichmäßig mit Wahrscheinlichkeit Eins gegen deren tatsächliche Verteilungsfunktion konvergieren und dass dadurch die Möglichkeit der Schätzung dieser Verteilungsfunktion gegeben ist.

Formulierung des Satzes im Einzelnen

Der Satz lässt sich angeben wie folgt:

Gegeben seien ein Wahrscheinlichkeitsraum

$(\Omega ,{\mathcal {A}},\operatorname {P} )$

und darauf eine Folge

$X_n \colon (\Omega, \mathcal{A} , \operatorname{P}) \to \R \; (n \in \N)$

von stochastisch unabhängigen und identisch verteilten Zufallsvariablen mit gemeinsamer Verteilungsfunktion $F\colon \mathbb {R} \to \mathbb {R}$ .

Die zum Stichprobenumfang $n\in \mathbb {N}$ gehörige empirische Verteilungsfunktion ist

$F_{n}\colon {\mathbb {R} \times \Omega }\to [0,1]$

mit

$F_{n}(x,\omega )={\frac {1}{n}}\cdot \sum _{k=1}^{n}{\chi _{(-\infty ,x]}(X_{k}(\omega ))}\;\;(x\in \mathbb {R} ,\omega \in \Omega ,)$ .

Hierzu hat man auf dem gegebenen Wahrscheinlichkeitsraum die Zufallsvariable

$D_n \colon \Omega \to \R$

mit

$D_n (\omega)=\sup_{x \in \R} \bigl| F_n (x,\omega) - F (x) \bigr|$ ,

welche die obere Grenze aller Abstände dieser empirischen Verteilung von der gemeinsamen Verteilung unter Berücksichtigung alle nur möglichen Ausprägungen $x\in \mathbb {R}$ angibt.

Dann gilt:

Die $D_{n}$ konvergieren mit Wahrscheinlichkeit 1, also fast sicher, gegen Null.

Es gilt also

$\operatorname{P} \bigl(\lim_{n \to \infty} D_n = 0 \bigr) = 1$ .

Anmerkungen

Der Satz ergibt sich als Anwendung des kolmogorowschen Gesetzes der großen Zahlen.
Er ist in verschiedene Richtungen verallgemeinert und abgewandelt worden. Einen Eindruck davon gibt die Arbeit des dänischen Mathematikers Flemming Topsøe aus dem Jahre 1970.

Basierend auf einem Artikel in:

Wikipedia.de