
Ungleichung
Eine Ungleichung ist ein Gegenstand der Mathematik, mit dem Größenvergleiche formuliert und untersucht werden können. Jede Ungleichung besteht aus zwei Termen, die durch eines der Vergleichszeichen < (Kleinerzeichen), ≤ (Kleinergleichzeichen), ≥ (Größergleichzeichen) oder > (Größerzeichen) verbunden sind.
Sind
und
zwei Terme, dann ist beispielsweise
eine Ungleichung. Man spricht „
kleiner (als)
“.
Wie bei einer Gleichung
heißt
die linke Seite und
die rechte Seite der Ungleichung.
Die in den beiden Termen auftretenden Werte sind meist reelle Zahlen. Die durch das Vergleichszeichen angesprochene Ordnungsrelation bezieht sich dann auf die natürliche Anordnung der reellen Zahlen.
Formen von Ungleichungen
Folgende fünf Formen von Ungleichungen sind möglich:
- (1)
(
kleiner
)
- (2)
(
kleiner oder gleich
)
- (3)
(
größer
)
- (4)
(
größer oder gleich
)
- (5)
(
ungleich
)
Die Form (5) entsteht durch Negation einer Gleichung. Sie wird daher in der Mathematik in der Regel nicht eigens thematisiert.
Ungleichungen sind Aussageformen. Die auf den beiden Seiten einer Ungleichung vorkommenden funktionalen Terme beinhalten in der Regel Variablen, welche stellvertretend für Elemente aus dem Definitionsbereich der jeweiligen Terme stehen. Werden diese Variablen durch feste Elemente der jeweiligen Definitionsbereiche ersetzt (Einsetzen), so entstehen Aussagen, welche entweder wahr oder falsch sind.
Umformung von Ungleichungen
Ähnlich wie bei Gleichungen ist es auch bei Ungleichungen möglich diese in äquivalente Ungleichungen umzuformen. Äquivalente Ungleichungen haben die gleichen Lösungsmengen, daher ist das Umformen von Ungleichungen wichtig zum Lösen von Ungleichungen, worauf der hierauf folgende Abschnitt eingehen wird. Die folgenden Gesetze werden für die Vergleichszeichen < und > dargestellt, sie gelten ganz analog auch für die Vergleichszeichen ≤, ≥ und ≠.
Umkehrbarkeit
Ungleichungen können umgekehrt werden:
Monotoniegesetze
Addition und Subtraktion
Für beliebige Terme ,
und
gilt:
- Es ist
genau dann, wenn
.
- Es ist
genau dann, wenn
.
Es dürfen also auf beiden Seiten einer Ungleichung die gleichen Terme addiert
oder subtrahiert werden, ohne dass sich die Lösungsmenge der Ungleichung ändert.
Beispielsweise vereinfacht sich die Ungleichung
durch Subtraktion des Terms
auf beiden Seiten zu der äquivalenten Ungleichung
.
Multiplikation und Division
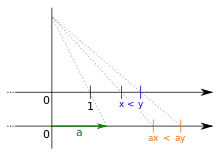

Für beliebige Terme ,
und
gilt:
- Aus
folgt
.
- Aus
folgt
.
- Aus
und
folgt
und
.
- Aus
und
, dann ist
und
.
Hier gilt demnach folgende Merkregel:
- Bei Punktrechnung mit einer reellen Zahl > 0 bleiben die Vergleichszeichen erhalten, während sie sich bei Punktrechnung mit einer reellen Zahl < 0 umkehren.
So sind zum Beispiel die Ungleichungen
und
äquivalent, wie man mit Hilfe von Division durch
sieht.
Anwenden einer Funktion
Durch Anwenden einer streng monotonen Funktion auf beide Seiten einer Ungleichung erhält man wieder eine Ungleichung mit derselben Lösungsmenge wie die Ausgangs-Ungleichung.
Ähnlich wie bei den Monotoniegesetzen allerdings muss auch hier unter Umständen das Vergleichszeichen gedreht werden. Wendet man nämlich eine streng monoton wachsende Funktion auf beide Seiten an, ändert sich das Vergleichszeichen dadurch nicht, wohl aber, wenn man eine streng monoton fallende Funktion benutzt: In diesem Fall muss das Vergleichszeichen < dann durch das entsprechend umgekehrte Zeichen > ersetzt werden, analog das Vergleichszeichen ≤ durch das ≥-Zeichen und umgekehrt.
Beispiele
Der natürliche
Logarithmus
und die Wurzelfunktion
sind streng monoton wachsende Funktionen und können daher, ohne dass man
dabei die Vergleichszeichen drehen müsste, zur Umformung von Ungleichungen
verwendet werden. Seien
zwei Terme, gilt dann dementsprechend zum Beispiel
Vorsicht dagegen ist geboten, wenn es sich um Exponentialfunktionen
handelt, die je nach ihrer Basis
streng monoton steigend, aber auch fallend sein können:
Gleiches gilt für Logarithmen beliebiger Exponenten:
Zum Beispiel:
Lösen von Ungleichungen
Eine Frage beim Umgang mit Ungleichungen ist - ähnlich wie bei der Lösung von Gleichungen - die Frage nach der Lösungsmenge der Ungleichung. Hier ist die Frage zu beantworten, ob und wenn ja welche Elemente der Definitionsbereiche beim Einsetzen in die beiden Terme eine wahre oder falsche Aussage liefern. Eine wichtige Technik zum Finden der Lösungsmenge ist das Umformen der Ungleichung in eine einfachere Form.
Bekannte Ungleichungen
In allen mathematischen Teilgebieten gibt es Sätze zur Gültigkeit von Ungleichungen. Das heißt, gewisse mathematische Aussagen sichern unter bestimmten Umständen die Richtigkeit einer vorgegebenen Ungleichung für eine gewisse Definitionsmenge. Im Folgenden werden einige wichtige Ungleichungen kurz erwähnt.
Dreiecksungleichung
Nach der Dreiecksungleichung ist im Dreieck
die Summe der Längen zweier Seiten
und
stets mindestens so groß wie die Länge der dritten Seite
.
Das heißt formal
.
Diese Ungleichung kann für viele mathematische Objekte verallgemeinert werden. Beispielsweise ist die Ungleichung
für die Betragsfunktion eine Verallgemeinerung der zuvor genannten Ungleichung und gilt für alle reellen Zahlen. Sie trägt ebenfalls den Namen Dreiecksungleichung. Diese Ungleichung kann auch für Betrag komplexer Zahlen oder für Integrale verallgemeinert werden (siehe Minkowski-Ungleichung).
Cauchy-Schwarz-Ungleichung
Sei
Prähilbertraum
also ein Vektorraum mit Skalarprodukt
und seien
und
Elemente aus
,
dann gilt immer die Ungleichung
Gleichheit gilt genau dann, wenn
und
linear
abhängig sind. Vektorräume mit Skalarprodukt treten in vielen mathematischen
Teilgebieten auf. Daher ist die Cauchy-Schwarz-Ungleichung auch in vielen
Teildisziplinen der Mathematik von Bedeutung, beispielsweise wird sie in der linearen Algebra, der
Integrationstheorie
und in der Wahrscheinlichkeitstheorie
verwendet.
Weitere Ungleichungen
- Bernoullische Ungleichung
- Bonferroni-Ungleichungen
- Jensensche Ungleichung
- Markow-Ungleichung
- Mittel-Ungleichung
- Tschebyschow-Ungleichung
- Unterschiedliche Ungleichungen, die nach Young benannt sind
Erweiterung des Begriffes
Bis jetzt wurden in diesem Artikel nur Ungleichungen betrachtet, deren Terme Werte in den reellen Zahlen annehmen. Der Ungleichungsbegriff wird gelegentlich – jedoch nicht einheitlich – zum Beispiel auf komplexe Zahlen, Vektoren oder Matrizen erweitert. Um Ungleichungen für diese Objekte betrachten zu können, müssen zuerst die vier Vergleichszeichen < , ≤, > und ≥ - im Folgenden auch Relationen genannt - für diese Objekte definiert werden.
Komplexe Zahlen
Die Menge der komplexen
Zahlen
ist zusammen mit der üblichen Addition und Multiplikation ein Körper, jedoch
ist es nicht möglich eine Relation ≤ so zu wählen, dass
zu einem geordneten
Körper wird. Das heißt, es ist nicht möglich, dass eine Relation auf
sowohl das Trichotomie-,
das Transitivitäts- und das Monotoniegesetz erfüllt. Jedoch wird manchmal eine
Relation, die durch
definiert ist, betrachtet. Hierbei bezeichnen
komplexe Zahlen und
den Realteil
beziehungsweise
den Imaginärteil
einer komplexen Zahl. Diese Definition der Relation erfüllt das Trichotomie- und
das Transitivitätsgesetz.
Spaltenvektoren
Auch für Spaltenvektoren
ist es möglich Relationen zu definieren. Seien
zwei Spaltenvektoren mit
und
wobei
and
reelle Zahlen sind. Relationen auf
kann man dann beispielsweise durch
und durch
definieren. Analog kann man auch die Relationen ≥ und > erklären. Hier ist
es allerdings nicht möglich, alle Elemente miteinander zu vergleichen.
Beispielsweise kann keines der vier Vergleichszeichen ein Verhältnis zwischen
den Elementen
und
beschreiben.
Weitere Beispiele
- Ist
, so definiert man
genau dann, wenn
positiv definit ist. Sind
, so gilt
genau dann, wenn
. Ähnlich können auch
oder
(semidefinit) definiert werden.
- Sei
ein reeller Banachraum und
ein Kegel. Sind
, so gilt
genau dann, wenn
.


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 24.09. 2022