Richtungsableitung

In der Mathematik ist die Richtungsableitung einer von mehreren Variablen abhängigen Funktion die momentane Änderungsrate dieser Funktion in einer durch einen Vektor vorgegebenen Richtung.

Eine Verallgemeinerung der Richtungsableitung auf unendlichdimensionale Räume ist das Gâteaux-Differential.

Definitionen

Seien $U\subset \mathbb{R} ^{n}$ eine offene Menge, $x\in {U}$ und $v\in \mathbb{R} ^{n}$ ein Vektor.

Die Richtungsableitung einer Funktion $f\colon {U}\to \mathbb{R}$ am Punkt in Richtung von ist definiert durch den Limes

$D_{{v}}{f(x)}=\lim _{{h\rightarrow 0}}{{\frac {f(x+h\cdot v)-f(x)}{h}}},$

falls dieser existiert.

Alternative Definition

Durch

$\gamma \colon (-\varepsilon ,\varepsilon )\to U,\;\gamma (t):=x+t\cdot v,$

ist ein Stück einer Parametergerade definiert. Das $\varepsilon >0$ ist hierbei hinreichend klein gewählt, so dass $\gamma (t)\in U$ an jeder Stelle $t\in (-\varepsilon ,\varepsilon )$ gilt.

Nun ist die Verkettung $f\circ \gamma$ eine gewöhnliche reelle Funktion und man erhält gemäß

$D_{v}f(x):=(f\circ \gamma )'(0)={\frac {\mathrm {d} }{\mathrm {d} t}}f(\gamma (t)){\Big |}_{t=0}$

eine äquivalente Definition der Richtungsableitung.

Diese Definition bietet den Vorteil der Zurückführung der Richtungsableitung auf eine gewöhnliche Ableitung, womit keine neue Art von Differentialquotient betrachtet werden muss.

Zudem kann man diese Definition dergestalt konzeptuell erweitern, dass $\gamma$ eine beliebige differenzierbare Parameterkurve mit $\gamma (0)=x$ und Tangentialvektor $\gamma '(0)=v$ sein darf. Allerdings setzt man hierfür als an der Stelle total differenzierbar voraus, denn dann ist das totale Differential $\mathrm df(x)$ vorhanden und es gilt

$(f\circ \gamma )'(0)=\mathrm {d} f(x)(v)$

gemäß der Kettenregel, was die Gewissheit verschafft, dass der Wert unabhängig von der gewählten Parameterkurve ist. Die Richtungsableitung ist in diesem Fall auch dann erklärt, wenn der Definitionsbereich von eine differenzierbare Mannigfaltigkeit ist und der Vektor aus dem Tangentialraum entstammt, welcher sich der Mannigfaltigkeit am Punkt anschmiegt. Beispielsweise kann die Spur der Parameterkurve bei einer Mannigfaltigkeit mit äußerer Krümmung unmöglich ein Geradenstück sein, weil sie per se innerhalb der Mannigfaltigkeit verlaufen muss.

Einseitige Richtungsableitungen

Die einseitigen Richtungsableitungen von $f\colon {U}\rightarrow {\mathbb {R}}$ in Richtung $v\in \mathbb{R} ^{{n}}$ sind definiert durch

$D_{v}^{{+}}{f(x)}=\lim _{{h\rightarrow 0,\,h>0}}{{\frac {f(x+h\cdot v)-f(x)}{h}}}$

$D_{v}^{{-}}{f(x)}=\lim _{{h\rightarrow 0,\,h<0}}{{\frac {f(x+h\cdot v)-f(x)}{h}}}=-D_{{-v}}^{+}f(x).$

Die Richtungsableitung in Richtung existiert genau dann, wenn die beiden einseitigen Richtungsableitungen $D_{{v}}^{{+}}{f(x)}$ und $D_{{v}}^{{-}}{f(x)}$ übereinstimmen. In diesem Fall gilt

$D_{{v}}{f(x)}=D_{{v}}^{{+}}{f(x)}=D_{{v}}^{{-}}{f(x)}.$

Ableitung in normierte Richtungen

Einige Autoren definieren die Richtungsableitung nur in Richtung normierter Vektoren:

$D_{{v}}{f(x)}=\lim _{{h\rightarrow 0}}{{\frac {f(x+h\cdot v)-f(x)}{h\cdot |v|}}}.$

Für Richtungen auf der Einheitssphäre ${\mathbb {S}}^{{n-1}}$ stimmen diese beiden Definition überein. Andernfalls unterscheiden sich die beiden Definitionen durch den Faktor |v| . Während die obige Definition für alle Richtungen definiert ist, ist die Ableitung in normierte Richtungen nur für $v\neq 0$ definiert.

Besonders in den Anwendungen kann es sinnvoll sein, mit dem normierten Richtungsvektor $\frac{v}{|v|}$ zu rechnen; damit ist gewährleistet, dass die Richtungsableitung nur mehr von der Richtung, aber nicht vom Betrag von abhängt.

Schreibweisen

Statt $D_{v}f(x)$ sind auch die Schreibweisen

$\nabla _{{v}}{f}(x)$ , $\partial _{v}f(x)$ , $\displaystyle {\frac {\partial {f(x)}}{\partial {v}}}$ und $f'_{v}(x)$

üblich, um unter anderem Verwechslungen mit den kovarianten Ableitungen der Differentialgeometrie zu vermeiden.

Ist total differenzierbar, so kann die Richtungsableitung mit Hilfe der totalen Ableitung dargestellt werden (siehe den Abschnitt Eigenschaften). Schreibweisen dafür sind

, $Df_{x}\,v$ , $\operatorname {grad}\ f(x)\cdot v$ , $\nabla f(x)\cdot v$ und $(v\cdot \nabla )f(x)$ .

Eigenschaften

Wählt man als Richtungsvektor ${\vec {v}}$ die Koordinateneinheitsvektoren ${\vec e}_{1},\dots ,{\vec e}_{n}$ , so erhält man die partiellen Ableitungen von im jeweiligen Punkt ${\vec {x}}$ :

$D_{{{\vec e}_{i}}}f({\vec x})={\frac {\partial f}{\partial x_{i}}}({\vec x})$
Die einseitige Richtungsableitung ist als Funktion von ${\vec {v}}$ positiv homogen, das heißt für alle positiven $\alpha >0$ gilt:

$D_{{\alpha {\vec {v}}}}^{{+}}{f({\vec {x}})}=\alpha D_{{{\vec {v}}}}^{{+}}{f({\vec {x}})}.$
Falls in ${\vec {x}}$ total differenzierbar ist, so ist die Richtungsableitung als Funktion von ${\vec {v}}$ sogar linear und kann durch den Gradienten $\nabla f$ von ausgedrückt werden:

$D_{{{\vec {v}}}}{f}({\vec x})=\nabla f({\vec x})\cdot {\vec {v}}={\frac {\partial f}{\partial x_{1}}}({\vec x})\,v_{1}+\dots +{\frac {\partial f}{\partial x_{n}}}({\vec x})\,v_{n}$

Beispiele

Eindimensionale Betragsfunktion

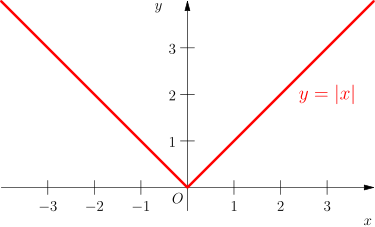
Absolutbetrag=seine Richtungsableitung in 0

Im eindimensionalen Fall gibt es nur zwei mögliche Richtungen, nämlich nach links bzw. nach rechts. Die Richtungsableitungen entsprechen also den üblichen einseitigen Ableitungen. Die Ableitungen in beide Richtungen dürfen verschiedene Werte annehmen, das bedeutet anschaulich, dass die Funktion einen Knick haben kann. Ein einfaches Beispiel hierfür ist die Betragsfunktion. Sie ist in $0$ zwar nicht differenzierbar, aber die einseitige Richtungsableitung existiert:

$D_{v}^{+}{f(0)}=v\quad$ für $v\geq 0$

und

$D_{v}^{-}{f(0)}=-v\quad$ für $v\leq 0$

Der Absolutbetrag ist also gleich seiner einseitigen Richtungsableitung in 0 als Funktion von .

Normalenableitung auf Gebieten

Ist $\Omega \subset \mathbb {R} ^{n}$ (n>1) ein glatt berandetes Gebiet mit einem äußeren Normalenvektorfeld $\nu$ und $f\in C^{1}({\bar \Omega })$ , dann ist

${\frac {\partial f}{\partial \nu }}=\nabla f\cdot \nu$

die Normalenableitung von auf dem Rand von $\Omega$ . Objekte dieser Art treten beispielsweise bei partiellen Differentialgleichungen mit Neumann-Randbedingungen auf.

Literatur

Otto Forster: Analysis 2. Differentialrechnung im Rⁿ. Gewöhnliche Differentialgleichungen. 7. Auflage. Vieweg-Verlag, 2006, ISBN 3-528-47231-6.
Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg 2000, ISBN 3-540-43580-8.

Basierend auf einem Artikel in:

Wikipedia.de