Schubmodul
| Physikalische Größe | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Schubmodul | |||||||||
| Formelzeichen | G | |||||||||
| ||||||||||
| Siehe auch: Elastizitätsmodul E
Spannung (Mechanik)
| ||||||||||
Der Schubmodul (auch Gleitmodul, G-Modul, Schermodul oder Torsionsmodul) ist eine Materialkonstante, die Auskunft gibt über die linear-elastische
Verformung eines Bauteils infolge einer Scherkraft oder Schubspannung.
Die SI-Einheit ist Newton pro Quadratmeter (1 N/m² = 1 Pa), also die Einheit einer mechanischen Spannung. In Materialdatenbanken wird der Schubmodul üblicherweise in N/mm² (=MPa) oder kN/mm² (=GPa) angegeben.
Im Rahmen der Elastizitätstheorie entspricht der Schubmodul
der zweiten Lamé-Konstanten und trägt dort das Symbol
.
Definition
Der Schubmodul beschreibt das Verhältnis zwischen der Schubspannung
und dem Tangens des Schubwinkels
(Gleitung):
Für kleine Winkel
kann in erster Näherung
gesetzt werden (Kleinwinkelnäherung).
Diese Formel ist analog zum Hooke’schen Gesetz für den 1-achsigen Spannungszustand:
Die Schubsteifigkeit ist das Produkt aus dem Schubmodul
des Werkstoffs und der Querschnittsfläche
:
| Material | Typische Werte für den Schubmodul in GPa (bei Raumtemperatur) |
|---|---|
| Stahl | 79,3–81 |
| Silicium (polykristallin) | 65 |
| Kupfer | 47 |
| Titan | 41,4 |
| Glas | 26,2 |
| Aluminium | 25,5 |
| Magnesium | 17 |
| Polyethylen | 0,117 |
| Gummi | 0,0003 |
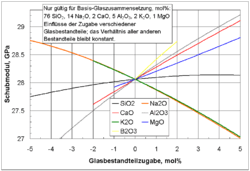
Einflüsse der Zugabe ausgewählter Glasbestandteile
zum Beispiel in
Der querschnittsabhängige Korrekturfaktor
berücksichtigt dabei die über den Querschnitt ungleichförmige Verteilung der Schubspannung
.
Oft wird die Schubsteifigkeit auch mithilfe der Schubfläche
ausgedrückt.
Bei Torsionsbelastung eines Bauteils berechnet sich seine
Torsionssteifigkeit aus dem Schubmodul und dem
Torsionsträgheitsmoment
,
das auf die Achse bezogen ist, um die der Körper tordiert wird:
analog zur Ermittlung der Dehnsteifigkeit (aus dem Produkt von Elastizitätsmodul und Querschnittsfläche).
Zusammenhang mit anderen Materialkonstanten
Bei einem isotropen Material steht der Schubmodul mit dem Elastizitätsmodul E, der Querkontraktionszahl ν (Poissonzahl) und dem Kompressionsmodul K in folgender Beziehung:
Für linear-elastisches, nicht-auxetisches Material ist die
Poissonzahl größer-gleich null. Aus der Energieerhaltung ergibt sich die positive Definitheit von
Kompressionsmodul und E-Modul. Daraus
folgt, dass die Poissonzahl unter 0,5 liegt.
Somit ergibt sich für den Schubmodul der meisten Materialien im linear-elastischen Bereich:
Auxetische Materialien sind so definiert, dass sie eine negative Poissonzahl haben, was nur bei wenigen Materialien der Fall ist. Da der Schubmodul aufgrund der Energieerhaltung eine positiv definite Größe hat, gilt für auxetische Materialien im linear-elastischen Bereich:
Da auch der E-Modul positiv definit ist, ergibt sich für die Poissonzahl der Gültigkeitsbereich
Umrechnung zwischen den elastischen Konstanten isotroper Festkörper
| Der Modul… | …ergibt sich aus: | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Kompressionsmodul
|
|
|
|
|
|||||||
| Elastizitätsmodul
|
|
|
|
|
|||||||
| 1. Lamé-Konstante
|
|
|
|
|
|||||||
| Schubmodul
(2. Lamé-Konstante) |
|
|
|
|
| ||||||
| Poissonzahl
|
|
|
|
|
|||||||
| Longitudinalmodul
|
|||||||||||
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.08. 2024