Projektiver Raum

Zentralprojektion einer Eisenbahnstrecke – die parallel verlaufenden Schienen scheinen sich im Fluchtpunkt am Horizont zu schneiden.

Der projektive Raum ist ein Begriff aus dem mathematischen Teilgebiet der Geometrie. Dieser Raum kann aufgefasst werden als die Menge aller Geraden durch den Ursprung eines Vektorraums . Ist der reelle zweidimensionale Vektorraum $\mathbb {R} ^{2}$ so nennt man ihn reelle projektive Gerade und im Falle $V=\mathbb {R} ^{3}$ heißt er reelle projektive Ebene. Analog definiert man projektive Geraden und projektive Ebenen über beliebigen Körpern als die Mengen der Ursprungsgeraden in einem zwei- bzw. dreidimensionalen Vektorraum über dem jeweiligen Körper. Projektive Ebenen können in der Inzidenzgeometrie auch axiomatisch charakterisiert werden, dabei erhält man auch projektive Ebenen, die nicht den Geraden in einem Vektorraum entsprechen.

Die Idee der projektiven Räume steht in Beziehung zur Zentralprojektion aus der darstellenden Geometrie und Kartenentwurfslehre, beziehungsweise zur Art und Weise, wie das Auge oder eine Kamera eine dreidimensionale Szene auf ein zweidimensionales Abbild projiziert. Alle Punkte, die gemeinsam mit der Linse der Kamera auf einer Linie liegen, werden auf einen gemeinsamen Punkt projiziert. In diesem Beispiel ist der zugrundeliegende Vektorraum der $\mathbb {R} ^{3}$ , die Kameralinse ist der Ursprung und der projektive Raum entspricht den Bildpunkten.

Definition

Der reell-projektive Raum $\mathbb {R} P^{n}$ ist die Menge aller Geraden durch den Nullpunkt im $\mathbb {R} ^{n+1}$ . Formal definiert man dies wie folgt.

Auf $\mathbb {R} ^{n+1}\setminus \{0\}$ sei die Äquivalenzrelation

$x\sim y\Leftrightarrow \exists \lambda \in \mathbb {R} \setminus \{0\}\colon x=\lambda y$

definiert. In Worten heißt dies, dass genau dann äquivalent zu ist, wenn es ein $\lambda \in \mathbb {R} \setminus \{0\}$ gibt, so dass $x=\lambda y$ gilt. Alle Punkte auf einer Ursprungsgeraden – der Ursprung ist nicht enthalten – werden also miteinander identifiziert und nicht mehr unterschieden.

Der Quotientenraum $\left(\mathbb{R} ^{{n+1}}\setminus \{0\}\right)/\sim$ mit der Quotiententopologie wird reeller, -dimensionaler projektiver Raum genannt und mit $\mathbb{R} P^{{n}}$ notiert.

Im Fall n=1 spricht man von der projektiven Geraden (auch: projektive Linie) und im Fall n=2 von einer projektiven Ebene.

Wählt man statt $\mathbb {R} ^{n+1}$ den komplexen Vektorraum $\mathbb{C} ^{{n+1}}$ , so erhält man mit der analogen Definition mit $\lambda \in \mathbb{C} \setminus \{0\}$ den komplex projektiven Raum der (komplexen) Dimension als den Raum der komplex eindimensionalen Unterräume des $\mathbb{C} ^{{n+1}}$ .

Die Koordinaten der Punkte des projektiven Raums, welche ja Äquivalenzklassen von Punkten $(x_{0},\ldots ,x_{n})\in \mathbb{R} ^{{n+1}}$ sind, werden durch $[x_{0}:\ldots :x_{n}]\in \mathbb{R} P^{n}$ notiert und heißen homogene Koordinaten. (Entsprechend für den komplex-projektiven Raum.) Für n=1 definiert die Abbildung $[x_{0}:x_{1}]\rightarrow {\frac {x_{0}}{x_{1}}}$ eine Bijektion zwischen $\mathbb{R} P^{1}$ und $\mathbb{R} \cup \left\{\infty \right\}$ .

Allgemeiner können auch projektive Räume über beliebigen anderen Körpern (an Stelle von $\mathbb {R}$ bzw. $\mathbb {C}$ ) konstruiert werden.

Ein allgemeinerer Begriff des projektiven Raumes wird in der synthetischen Geometrie verwendet, vor allem für den Fall n=2 die projektive Ebene. Die Axiomatik dieses allgemeineren Begriffes wird im Hauptartikel Projektive Geometrie dargestellt.

Projektive lineare Gruppe (Kollineationen)

→ Hauptartikel: Projektive Abbildung

Die projektive lineare Gruppe $\mathrm{PGL}(n+1,\mathbb \R)$ ist die Gruppe der invertierbaren projektiven Abbildungen, sie ist definiert als Quotient von $\mathrm{GL}(n+1, \mathbb \R)$ unter der Äquivalenzrelation

$A\sim B\Leftrightarrow \exists \lambda \in \mathbb{R} \setminus \{0\}\colon A=\lambda B$ .

Die Wirkung von $\mathrm{GL}(n+1 , \mathbb \R)$ auf $\left(\mathbb{R} ^{{n+1}}\setminus \{0\}\right)$ gibt eine wohl-definierte Wirkung von $\mathrm{PGL}(n+1,\mathbb \R)$ auf $\mathbb {R} P^{n}$ . Die den Elementen $A\in PGL(n+1,{\mathbb R})$ entsprechenden Abbildungen $A:\mathbb{R} P^{n}\rightarrow \mathbb{R} P^{n}$ sind projektive, das heißt hier doppelverhältnistreue Kollineationen. Mit anderen Worten:

Sie bilden die Menge der projektiven Punkte bijektiv auf sich selbst ab.
Sie bilden jede Gerade als Punktmenge auf eine Gerade ab (erhalten damit die Inzidenzstruktur).
Das Doppelverhältnis von beliebigen 4 Punkten, die auf einer Geraden liegen, bleibt unverändert. Das unterscheidet Projektivitäten von bijektiven echt semilinearen Selbstabbildungen des Vektorraums.

Analog definiert man eine Wirkung von $\mathrm{PGL}(n+1,\mathbb \C)$ auf $\mathbb{C} P^{n}$ .

Im Fall der projektiven Gerade wirkt $\mathrm{PGL}(2,\mathbb \R)$ auf $\mathbb{R} P^{1}$ durch gebrochen-lineare Transformationen. Nach der Identifikation von $\mathbb{R} P^{1}$ mit $\mathbb{R} \cup \left\{\infty \right\}$ (bzw. $\mathbb{C} P^{1}$ mit $\mathbb{C} \cup \left\{\infty \right\}$ ) wirkt $\mathrm{PGL}(2,\mathbb \R)$ bzw. $\mathrm{PGL}(2,\mathbb \R)$ durch $\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)z={\frac {az+b}{cz+d}}$ .

Beispiel: Riemann’sche Zahlenkugel

Stereographische Rückprojektionen der komplexen Zahlen und auf die Punkte $\alpha$ und $\beta$ der Riemann’schen Zahlenkugel

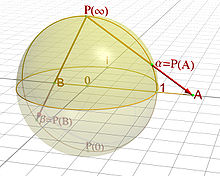
Die komplex-projektive Gerade ist nach obiger Definition gerade die Menge der komplexen Geraden in ${\mathbb C}^{2}$ , welche durch den Ursprung $(0,0)\in {\mathbb C}^{2}$ gehen.

Die komplex-projektive Gerade kann man auch als die reell-zweidimensionale Sphäre beziehungsweise Riemann’sche Zahlenkugel

$S^{2}=\{(x,y,z)\in {\mathbb R}^{3},x^{2}+y^{2}+z^{2}=1\}$

auffassen. Die Übereinstimmung mit obigen Begriffen ergibt sich wie folgt: Bezeichne mit $N:=(0,0,1)\in S^{2}$ den „Nordpol“. Betrachte die stereographische Projektion

$f:S^{2}\setminus \{N\}\rightarrow {\mathbb R}^{2}\cong {\mathbb C},$

welche durch $\textstyle (x,y,z)\mapsto \left({\frac {x}{1-z}},{\frac {y}{1-z}}\right)={\frac {x+iy}{1-z}}$ gegeben ist. Anschaulich legt man durch (x,y,z) und den Nordpol eine (reelle) Gerade und wählt den Schnittpunkt dieser Geraden mit der Äquatorebene als Bildpunkt der Abbildung, wobei der Nordpol mit $\infty$ identifiziert wird. Die Korrespondenz zwischen $S^{2}$ und ${\mathbb C}P^{1}$ in homogenen Koordinaten ist dann $(x,y,z)\mapsto \left[1:{\frac {x+iy}{1-z}}\right]=[1-z:x+iy]$ .

Eigenschaften

Die reellen und komplexen projektiven Räume sind kompakte Mannigfaltigkeiten.
Der projektive Raum ist ein Beispiel für eine nicht affine algebraische Varietät bzw. ein nicht affines Schema. Außerdem hat der projektive Raum die Struktur einer torischen Varietät. Im algebraisch-geometrischen Kontext kann man anstelle der reellen oder komplexen Zahlen jeden beliebigen Körper einsetzen.
Untervarietäten des projektiven Raums werden als projektive Varietäten (veraltet auch als projektive Mannigfaltigkeiten) bezeichnet.
Lokal nach dem projektiven Raum modellierte lokal-homogene Mannigfaltigkeiten werden als projektive Mannigfaltigkeiten bezeichnet.

Topologie

Die projektive Gerade $\mathbb{R} P^{1}$ ist homöomorph zum Kreis $S^{1}$ . Für n>1 ist die Fundamentalgruppe des projektiven Raums $\mathbb {R} P^{n}$ die Gruppe Z/2Z, die 2-fache Überlagerung des $\mathbb {R} P^{n}$ ist die Sphäre $\mathbb {S} ^{n}$ .

Für ungerade n ist der $\mathbb {R} P^{n}$ orientierbar, für gerade n ist er nicht orientierbar.

Die projektive Ebene $\mathbb {R} P^{2}$ ist eine nicht-orientierbare Fläche, die sich nicht in den $\mathbb {R} ^{3}$ einbetten lässt. Es gibt aber Immersionen des $\mathbb {R} P^{2}$ in den $\mathbb {R} ^{3}$ , zum Beispiel die sogenannte Boysche Fläche.

Die komplex-projektive Gerade $\mathbb{C} P^{1}$ ist homöomorph zur Sphäre $S^{2}$ , die quaternionisch-projektive Gerade $\mathbb{H} P^{1}$ ist homöomorph zur $S^{4}$ , die Cayley-projektive Gerade $CaP^{1}$ homöomorph zur $S^{8}$ .

Alle komplex- oder quaternionisch-projektiven Räume sind einfach zusammenhängend.

Die Hopf-Faserungen bilden (für ${\mathbb K}=\mathbb{C} ,\mathbb{H} ,Ca$ ) jeweils die Einheitssphäre in ${\mathbb K}^{2}$ auf ${\mathbb K}P^{1}$ ab, die Faser ist die Einheitssphäre in ${\mathbb K}^{1}$ . Man erhält auf diese Weise Faserungen

$S^{1}\rightarrow S^{3}\rightarrow S^{2},S^{3}\rightarrow S^{7}\rightarrow S^{4},S^{7}\rightarrow S^{{15}}\rightarrow S^{8}$ .

Diese Faserungen haben Hopf-Invariante 1.

Projektive Teilräume und abgeleitete Räume

In diesem Abschnitt wird im Sinne der obigen allgemeineren Definition von einem dimensionalen projektiven Raum $KP^{n}$ über einem beliebigen Körper ausgegangen, die Punkte des Raumes können also als eindimensionale Untervektorräume von $K^{{n+1}}$ angesehen werden.

Jedem -dimensionalen Unterraum $(-1\leq k\leq n)$ von $K^{{n+1}}$ ist ein -dimensionaler projektiver Teilraum von $KP^{n}$ zugeordnet. Man nennt auch eine (verallgemeinerte, projektive) Ebene, für Hyperebene, für Gerade in $KP^{n}$ . Auch die leere Menge wird hier als projektiver Teilraum betrachtet, dem der Nullraum von $K^{{n+1}}$ und als Dimension zugeordnet wird.
Die Schnittmenge von zwei projektiven Teilräumen ist wiederum ein projektiver Teilraum.
Bildet man zu den Unterräumen, die zwei projektiven Räumen $S_{1}$ und $S_{2}$ zugeordnet sind, die lineare Hülle ihrer Vereinigungsmenge in $K^{{n+1}}$ , so gehört zu diesem Untervektorraum wieder ein projektiver Teilraum, der Verbindungsraum $S_{1}\vee S_{2}$ (auch als Summe $S_{1}+S_{2}$ notiert) von $S_{1}$ und $S_{2}$ .
Für Schnitt und Verbindung von projektiven Teilräumen gilt die projektive Dimensionsformel:

$\operatorname {dim}(S_{1})+\operatorname {dim}(S_{2})=\operatorname {dim}(S_{1}\vee S_{2})+\operatorname {dim}(S_{1}\cap S_{2})$ .

Die Menge ${\mathcal {P}}^{n}$ aller Teilräume des projektiven Raumes $KP^{n}$ bildet bezüglich der Verknüpfungen „Schnitt“ $\cap$ und „Verbindung“ $\vee$ einen längenendlichen, modularen, komplementären Verband.
Jedem projektiven Punkt kann über seine Koordinaten eine homogene Koordinatengleichung zugeordnet werden, deren Lösungsmenge eine Hyperebene beschreibt. Durch die so definierten Hyperebenenkoordinaten bilden die Hyperebenen in $KP^{n}$ wiederum Punkte eines projektiven Raumes, des Dualraums $(KP^{n})^{D}$ .(→ siehe dazu Projektives Koordinatensystem#Koordinatengleichungen und Hyperebenenkoordinaten).
Allgemeiner bildet die Menge der Hyperebenen, die einen festen -dimensionalen Teilraum enthalten, einen projektiven Raum, den man als Bündel, im Spezialfall als Büschel von Hyperebenen bezeichnet. heißt Träger des Bündels oder Büschels.

Basierend auf einem Artikel in:

Wikipedia.de