
Quadraturamplitudenmodulation
Die Quadraturamplitudenmodulation, oder Quadratur-Amplituden-Modulation (Abkürzung QAM, englisch Quadrature amplitude modulation), ist ein Modulationsverfahren in der elektronischen Nachrichtentechnik, das die Amplitudenmodulation und Phasenmodulation kombiniert. Sie wird in der Fachliteratur überwiegend zu den digitalen Modulationsverfahren gezählt, wenngleich auch Formen der analogen Quadraturamplitudenmodulation unter der Bezeichnung Quadraturmodulation existieren.
Allgemeines
Bei der QAM wird der Träger mit Kreisfrequenz ω zweifach mit 90° Phasenverschiebung („in Quadratur“) verwendet. Darauf werden mittels multiplikativer Mischung zwei unabhängige Basisbandsignale aufmoduliert. Anschließend werden die beiden modulierten Signale addiert, um das Sendesignal zu erhalten. Dabei kann das Amplitudenmodulieren zweier Träger in Quadratur ebenfalls als Amplituden- und Phasenmodulieren eines einzigen Trägers verstanden werden. Die beiden Basisbandsignale werden in der englischsprachigen Literatur auch als I für In-phase component und Q für Quadrature Component bezeichnet (I&Q-Verfahren), wovon sich die Bezeichnung IQ-Modulation ableitet. Dabei spielt es keine Rolle, ob die beiden Basisbandsignale zeit- und wertkontinuierlich sind, wie beispielsweise die analogen Farbdifferenzsignale beim analogen Fernsehen, oder im Rahmen der digitalen QAM eine kontinuierliche Aneinanderreihung von Symbolen darstellen.
Die beiden Basisbandsignale I und Q können unabhängig oder voneinander abhängig gewählt werden. Sind die beiden Basissignale voneinander nach bestimmten Regeln abhängig, spricht man nicht mehr von einer QAM, obwohl eine unveränderte Modulatorstruktur vorliegt. Durch die Art der Abhängigkeit lassen sich mit dieser Modulatorstruktur alle linearen und nichtlinearen Modulationsformen, wie die Amplitudenmodulation (AM), Winkelmodulationen wie die Frequenzmodulation (FM) oder auch Einseitenbandmodulationen wie SSB oder VSB-Modulation realisieren. Software Defined Radios machen sich diesen Umstand zunutze.
Tragen die beiden Basisbandsignale I und Q voneinander unabhängige Informationen, streng genommen spricht man nur in diesem Fall von der QAM, muss zur Demodulation im Empfänger der Träger nicht nur mit der gleichen Frequenz wie beim Modulator vorliegen, sondern auch in identischer Phasenlage. Dies wird auch als kohärente Demodulation bezeichnet. Bei nicht korrekter Phasenlage würden sich Teile der beiden unabhängigen Basisbandsignale überlagern und daher eine korrekte Rekonstruktion des Sendesignals im Empfänger verhindern.
Die korrekte Phasenlage ist dabei durch zusätzliche Verfahren sicherzustellen, die über das Modulationsverfahren hinausgehen; die Verfahren dazu richten sich nach der jeweiligen Anwendung. Beispielsweise werden bei analogen QAM-Verfahren Burst-Signale, wie bei den Farbdifferenzsignalen, oder zusätzliche Pilottöne verwendet. Im Bereich der digitalen Signalübertragung werden periodisch spezielle Synchronisationssequenzen im Datenstrom übertragen, die dem Empfänger bekannt sind. Der Empfänger justiert im Rahmen der Synchronisierung solange die Phasenlage im Demodulator, bis die bekannten Synchronisationssequenzen passend empfangen werden.
Wegen des schaltungstechnisch größeren Aufwandes auf Empfängerseite findet die QAM-Modulation als analoge Quadraturmodulation nur in speziellen Bereichen Anwendung. Beispiele sind das AM-Stereo-Verfahren und die Übertragung der beiden Farbdifferenzsignale bei analogem Farbfernsehen nach dem NTSC- bzw. nach dem PAL-Verfahren.
Die Mehrzahl aller Anwendungen der QAM liegen im Bereich der digitalen Signalübertragung, wo digitale Datenströme zunächst auf den I- und Q-Zweig aufgeteilt werden. Den einzelnen Bits werden bestimmte Symbole zugeordnet und diese Symbolfolgen durch Pulsformungsfilter in einen kontinuierlichen Signalverlauf der beiden Basisbandsignale I und Q umgewandelt.
Weiterentwicklungen der QAM im Rahmen der digitalen Signalverarbeitung führen zu der codierten Modulation wie der Trellis-Coded Modulation (TCM), wo die Kanalcodierung, beispielsweise ein Faltungscode, mit dem Modulationsverfahren, wie unter anderem der QAM, funktionell „verschmilzt“.
Anwendungen der QAM im Rahmen der digitalen Signalverarbeitung liegen beispielsweise bei Modems zur Datenübertragung und im Bereich von Mehrträgerverfahren wie der DSL-Technik, dabei werden auch Varianten wie die Carrier-less Amplitude/Phase Modulation (CAP) eingesetzt. Weitere Anwendungsbereiche der QAM liegen bei COFDM, wo sie als Basismodulationsverfahren dient und unter anderem bei den digitalen terrestrischen Fernsehnormen nach DVB-T und DVB-T2 vorkommt.
Mathematischer Hintergrund
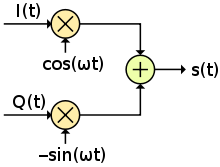
Das Sendesignal wird, wie in nebenstehender Abbildung dargestellt,
durch folgende Beziehung
aus den beiden Basisbandsignalen und
im Modulator gebildet.
Die Kreisfrequenz
steht für die
Trägerfrequenz
.
kann auch mithilfe der
Phase
sowie der
Amplitude
des Signales dargestellt werden:
Die Demodulation setzt eine zum Sender identisch eingestellte Phasenlage voraus. Liegt ein
störungsfreier Übertragungskanal vor,
ist das Empfangssignal gleich dem Sendesignal
, andernfalls kommen
Fehleranteile
zu dem Empfangssignal dazu:
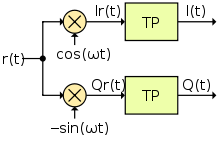
Das Fehlersignal wird unter anderem durch das Kanalmodell beschrieben. Im fehlerfreien Fall mit gilt für die Gewinnung des
Basisbandsignals
:
Dabei entstehen im Signal neben dem gewünschten Basisbandsignal
zusätzlich Mischprodukte mit doppelter Frequenz.
Diese oberen, unerwünschten Frequenzanteile werden durch einen nachfolgenden
Tiefpassfilter (TP) weggefiltert, wodurch am Ausgang
des Demodulators das ursprüngliche Signal
gebildet wird.
Die Bildung von verläuft analog:
und einer nachfolgenden Tiefpassfilterung zur Bildung von . Der bei
und
auftretende
konstante Faktor von 1/2 kann durch eine Verstärkung kompensiert werden.
Quantisierte QAM
Die quantisierte QAM erweitert die oben allgemein dargestellte QAM um Verfahren zur Übertragung von wert- und zeitdiskreten Signalfolgen, auch als Digitalsignal bezeichnet.
Konstellationsdiagramm
Grundsätzlich wird bei digitalen QAM zwischen orthogonalen Rastern und nicht orthogonalen Rastern unterschieden.
Die beiden Basisbandsignale I und Q in Bandpasslage stehen immer
orthogonal aufeinander, was die Darstellung
der Symbole in der komplexen Ebene
in Form eines Konstellationsdiagramms
erlaubt. Im Konstellationsdiagram entspricht die einem Symbol zugehörige Amplitude der Länge des Vektors
und die Phasenlage entspricht dem Winkel zwischen der I-Achse und jenem Vektor.
Ist die Phasenlage bei dem Empfänger nicht korrekt auf die Phasenlage des Senders abgestimmt, kommt es zu einer Drehung des
Konstellationsdiagramms in der komplexen Ebene, mit der Folge entsprechender Empfangsfehler.
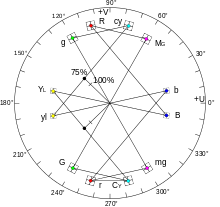
Die Anzahl der verfügbaren Symbole, sie stellen Punkte bzw. Bereiche in dieser komplexen Ebene dar, wird in Form einer Zahl ausgedrückt. Beispielsweise in der Angabe 64-QAM für eine QAM mit einem Umfang von 64 Symbolen.
Die Anzahl der Symbole in der komplexen I/Q-Ebene ist bei binären Übertragungen eine Zweierpotenz, um den einzelnen Symbolen eine bestimmte Anzahl an Bits zuzuordnen (Bits pro Symbol/Bitrate). Für eine hohe spektrale Effizienz, und so dies durch ein genügend großes Signal-Rausch-Verhältnis (SNR) möglich ist, wird eine große Anzahl von Symbolen verwendet. Beispiele für QAM-Konstellationen mit gerader Bitanzahl bei binärer Symbolzuordnung sind:
- 2 Bit: 4-QAM – diese ist identisch zur QPSK bzw. 4-PSK und verwendet 4 Punkte in einem 2×2-Raster bzw. auf einem Kreis, Anwendung bei DVB-S.
- 4 Bit: Bei 16-QAM werden 16 Symbole verwendet, beispielsweise Anwendung bei ITU-R Norm V.29 und bei DVB-T
- 6 Bit: Bei 64-QAM werden 64 Symbole verwendet, Anwendung bei DVB-C und bei DVB-T
- 8 Bit: Bei 256-QAM werden 256 Symbole verwendet, Anwendung bei DVB-C
- 10 Bit: 1024-QAM
- 12 Bit: 4096-QAM. Dies ist die größte, im Rahmen der Spezifikation von DVB-C2 derzeit angedachte QAM-Konstellation, die unter besten Voraussetzungen – bei einem Störabstand von 36 dB – gerade noch detektierbar ist. Auch der ITU-T-Standard G.hn verwendet, neben einer umfangreichen Kanalcodierung, eine 4096-QAM
Im Fall einer ungeraden Anzahl von Bits pro Symbol kann die erforderliche Einordnung in das Zweierpotenz-Raster durch eine Reduktion desjenigen Konstellationsraumes erreicht werden, der durch die nächsthöhere Quadratzahl aufgespannt wird. Es ist damit in vielen Fällen eine Verschlechterung der Fehlerrate verbunden, weshalb diese QAM-Konstellationen seltener verwendet werden. Ein Anwendungsbeispiel liegt in Kombination mit den Low-Density-Parity-Check-Codes (LDPC) mit einer 8-QAM vor, wo sich in Kombination mit der LDPC-Codierung eine bessere Gesamteffizienz als mit anderen QAM-Konstellationen ergibt.
- 3 Bit: Bei 8-QAM sind das 8 Punkte (9 Punkte in einem 3×3-Raster abzüglich der Mittelposition ergeben die 8 benötigten Positionen – diese Modulation ist ähnlich zur 8-PSK)
- 5 Bit: Bei 32-QAM sind das 32 Punkte (36 Punkte in einem 6×6-Raster abzüglich je einer Position pro Eckpunkt ergeben die 32 benötigten Positionen)
Die nicht orthogonalen Rasteranordnungen bei QAM können Vorteile bei der Symbolsynchronisation auf Seiten des Empfängers bieten. Bei hoher Fehlerrate können deshalb bestimmte Symbole vergleichsweise einfach aus dem Konstellationsdiagramm dynamisch entfernt werden. Die damit verbundene Bitratenreduktion verringert die Wahrscheinlichkeit von Übertragungsfehlern im Nutzsignal. Der Nachteil aller nicht orthogonalen QAMs besteht jedoch im Vergleich zur orthogonalen Symbolanordnung in einer schlechteren spektralen Effizienz. Dies ist Folge des Verzichts auf die Ausnutzung der höchstmöglichen Packungsdichte der Symbolanordnung in der komplexen Ebene.
Für Bereiche mit hohen Störpegeln werden Konstellationen mit geringer Symbolanzahl gewählt. In fast allen Fällen kommt eine zusätzliche Kanalcodierung wie ein Faltungscode zwecks Korrektur von Übertragungsfehlern zur Anwendung.
 16-QAM mit zulässigen Bereichen in denen eine eindeutige Symbolerkennung möglich ist
16-QAM mit zulässigen Bereichen in denen eine eindeutige Symbolerkennung möglich ist Konstellationspunkte einer 256-QAM
Konstellationspunkte einer 256-QAM Durch nicht korrekt eingestellte Phasenlage um 3,57 Grad gedrehte Konstellationspunkte einer 256-QAM. Bereits diese geringe Drehung würde bei 256-QAM zu massiven Übertragungsfehlern führen
Durch nicht korrekt eingestellte Phasenlage um 3,57 Grad gedrehte Konstellationspunkte einer 256-QAM. Bereits diese geringe Drehung würde bei 256-QAM zu massiven Übertragungsfehlern führen Nicht orthogonale QAM wie sie bei Fax-Geräten nach der Norm V.29 verwendet wird
Nicht orthogonale QAM wie sie bei Fax-Geräten nach der Norm V.29 verwendet wird
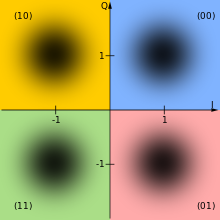
- 4-QAM-Empfangssymbole mit additivem Gauß’schen Rauschen (AWGN) der Varianzen 0,01, 0,1 und 0,3
 Rauschvarianz 0,01
Rauschvarianz 0,01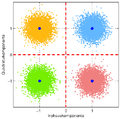 Rauschvarianz 0,1
Rauschvarianz 0,1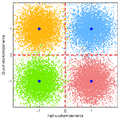 Rauschvarianz 0,3
Rauschvarianz 0,3
Es wurden jeweils 5000 verrauschte Empfangswerte je 4-QAM-Symbol erzeugt. Bei einer Varianz des Rauschens von 0,3 sind Empfangswerte zu erkennen, die nicht im passenden Quadranten liegen. Bei einer Entscheidung führt dies zu einem Symbolfehler. Die Zahl der falsch übertragenden Bits hängt von der verwendeten Bit-Symbol-Zuordnung (Bit-Mapping) ab.
Zuordnungen

Die Zuordnung der Bitfolgen zu den einzelnen Sendesymbolen im Konstellationsdiagramm kann zeitlich statisch oder dynamisch nach bestimmten Regeln erfolgen.
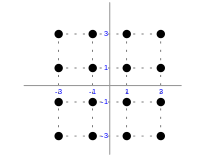
Eine statische Zuordnung erfolgt üblicherweise so, dass benachbarte Symbole sich möglichst nur um ein Bit unterscheiden, wie in nebenstehender Abbildung dargestellt. Für die systematische Verteilung der Bitfolgen in dem Konstellationsdiagramm kann unter anderem der Gray-Code eingesetzt werden. Die wesentliche Eigenschaft dieses Codes ist, dass sich bei jedem Schritt nur ein Bit ändert.
Diese Zuordnung erlaubt eine effizientere Korrektur von Übertragungsfehlern. Das Signal wird bei der Übertragung durch Rauschen überlagert, welches zu einer Streuung der Signalpunkte führt. Für übliche Wahrscheinlichkeitsverteilungen des Rauschens (wie die Gauß-Verteilung) ist es am wahrscheinlichsten, dass ein Signalpunkt in die Nähe eines direkt benachbarten Signalpunktes verschoben wird. Durch die Gray-Codierung ist sichergestellt, dass bei derartigen Fehlern nur ein Bit falsch ist. Die absolute Anzahl der Bitfehler wird so minimiert und einer optional vorhandenen Vorwärtsfehlerkorrektur (FEC) besser zugänglich.
Dynamische Zuordnungen finden im Rahmen der codierten Modulation Anwendung. In diesen Fällen ist die Zuordnung der Bitmuster unter anderem von den vorherigen Zuständen bzw. Symbolkombinationen abhängig. Ein Beispiel für eine dynamische Bitzuordnung im Konstellationsdiagramm stellt die bereits eingangs erwähnte Trellis-Coded Modulation dar.
Modulatorstruktur
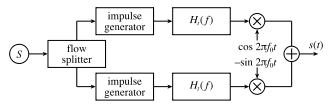
Bei der quantisierten QAM wird die oben dargestellte allgemeine Modulatorstruktur zur Übertragung von Datenfolgen um folgende Funktionsblöcke erweitert, wie auch in nebenstehender Abbildung dargestellt:
- Einen Splitter, der den von der Datenquelle S erzeugten Datenstrom in zwei Datenströme für I und Q mit jeweils halber Bitrate aufteilt.
- Für jeden Zweig ist je ein Impulsgenerator vorgesehen. Dieser weist einer bestimmten Anzahl von Bits, abhängig vom Symbolumfang, ein bestimmtes Signalniveau an seinem Ausgang zu. Beispielsweise werden bei 16-QAM je Zweig je 2 Bits vom Impulsgenerator zusammengefasst und bilden dann 4 Stufen mit den bipolaren Niveaus −3, −1, 1 und 3. Diese Zahlenwerte entsprechen direkt den entsprechenden Auslenkungen auf der I- bzw. Q-Achse im Konstellationsdiagramm.
- Bei dem schlagartigen Wechsel zwischen zwei unterschiedlichen Niveaus tritt am Ausgang des Impulsgenerators ein Sprung auf, der unerwünschte spektrale Störanteile aufweist. Zwecks Minimierung werden diese Impulse in einem Impulsformungsfilter H "geformt", um einen möglichst gleichmäßigen Verlauf der I- bzw. Q-Komponente zu erhalten. Dafür werden Pulsformungsfilter wie das Raised-Cosine-Filter oder der Gauß-Filter verwendet.
Die Impulsdauer, die bei 16-QAM die Information von 4 Bits trägt, richtet sich nach der Bandbreite des Übertragungskanals. Steht eine große Bandbreite zur Verfügung, können die Symbole zeitlich knapper übertragen werden als bei geringer Bandbreite. Bei gegebener Bandbreite richtet sich die maximale Symbolrate nach der Intersymbolinterferenz, die im Idealfall gerade noch nicht auftreten darf, da sie die Unterscheidung der zeitlich aufeinanderfolgenden Symbole verhindert.
Demodulatorstruktur
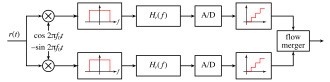
Der Empfänger für quantisierte QAM stellt das Gegenstück zum Sender dar. Die aus den Tiefpassfiltern gewonnenen Basisbandsignale I und Q werden je einem Matched Filter H zugeführt. Die Übertragungsfunktion dieses Filters ist auf die vom Sender gebildeten Pulsformen ausgelegt und erlaubt damit eine optimale Störunterdrückung.
Diese beiden Signale werden je einem Analog-Digital-Umsetzer (ADC) zugeführt. Die unterschiedlich hohen Niveaus des sendeseitigen Impulsgenerators werden in der nächsten Stufe in die zugehörigen Bitkombinationen umgesetzt. Anschließend erfolgt die Zusammensetzung der beiden Datenströme zur weiteren Datenverarbeitung.
Literatur
- Hermann Rohling: Einführung in die Informations- und Codierungstheorie. Teubner Verlag, Stuttgart 1995, ISBN 3-519-06174-0.
- Karl-Dirk Kammeyer: Nachrichtenübertragung. 4. neu bearbeitete und ergänzte Auflage. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8351-0179-1.
- John G. Proakis, Masoud Salehi: Communication Systems Engineering. 2. Auflage. Prentice Hall, Upper Saddle River NJ 2002, ISBN 0-13-095007-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.02. 2023