Pseudorapidität

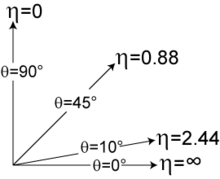
Gegenüberstellung von Polarwinkel $\theta$ und Pseudorapidität $\eta$ für einige beispielhafte Werte.
Als Vorwärtsrichtung bezeichnet man den Winkelbereich mit großen Werten von $\eta$ .

Die Pseudorapidität $\eta$ (eta) ist eine räumliche Koordinate, die in der experimentellen Teilchenphysik verwendet wird, um den Winkel eines Vektors relativ zur Strahlachse anzugeben. Sie wird gegenüber der Angabe des Polarwinkels $\theta$ bevorzugt, weil bei Hadron-Hadron-Kollisionen der Fluss der erzeugten Teilchen pro Pseudorapiditäts-Intervall etwa konstant ist.

Die Pseudorapidität ist definiert als

$\eta =-\ln \left[\tan \left({\frac {\theta }{2}}\right)\right].$

Für ein Teilchen mit Impuls ${\vec {p}}$ (und $\left|{\vec {p}}\right|=p$ ) lässt sich dies umschreiben in:

$\eta =\operatorname {artanh} (p_{L}/p)={\frac {1}{2}}\cdot \ln \left({\frac {p+p_{L}}{p-p_{L}}}\right),$

worin

$\operatorname {artanh}$ die Areatangens-hyperbolicus-Funktion ist und
der Longitudinalimpuls $p_{L}$ die Impulskomponente entlang der Strahlachse.

In der Hochenergienäherung, d.h. für ein Teilchen mit der Energie , dessen Masse gegenüber seinem Impuls vernachlässigbar ist, $m\ll p\Rightarrow E\approx p$ , ist die Pseudorapidität numerisch in etwa gleich der Rapidität

$\eta \approx y,$

die in der experimentellen Teilchenphysik definiert wird als

$y={\frac {1}{2}}\cdot \ln \left({\frac {E+p_{L}}{E-p_{L}}}\right).$

Zum Vergleich: die originale Rapidität gemäß der speziellen Relativitätstheorie ist

$\vartheta ={\frac {1}{2}}\cdot \ln \left({\frac {E+p}{E-p}}\right)={\frac {1}{2}}\cdot \ln \left({\frac {1+\beta }{1-\beta }}\right),$

worin $\beta =v/c$ das Verhältnis der Teilchengeschwindigkeit zur Lichtgeschwindigkeit ist.

Die Form des differentiellen Wirkungsquerschnitts $d\sigma /dy$ ist invariant unter einem Lorentz-Boost. Das Gleiche gilt in guter Näherung auch für die Pseudorapidität, nur ist diese leichter zu messen: Nicht die Masse des Teilchens muss ermittelt werden, sondern lediglich seine Flugrichtung durch den Detektor.

Basierend auf einem Artikel in:

Wikipedia.de