Rayleigh-Streuung

Die Rayleigh-Streuung ist die Ursache der Luftperspektive

Die Rayleigh-Streuung verursacht den blauen Farbton des Himmels am Tag und die Rotfärbung der Sonne, wenn sie unter- oder aufgeht.

Rayleigh-Streuung eines grünen 50-mW-Laserpointers bei Vollmond

Die Rayleigh-Streuung [ˈreɪlɪ-], benannt nach John William Strutt, 3. Baron Rayleigh, bezeichnet die (hauptsächlich) elastische Streuung elektromagnetischer Wellen an Teilchen, deren Durchmesser klein im Vergleich zur Wellenlänge λ ist, also etwa bei der Streuung von Licht an kleinen Molekülen. Bei Streuung in der Erdatmosphäre an molekularem Sauerstoff und Stickstoff wird typischerweise auch die inelastische Komponente durch Rotationsramanstreuung mit zur Rayleigh-Streuung gezählt, da diese nur eine Verschiebung der Wellenzahl des Photons um weniger als 50 cm⁻¹ bewirkt. Der Wirkungsquerschnitt dieses Beitrags hat die gleiche Wellenlängenabhängigkeit wie die elastische Komponente.

Der Streuquerschnitt σ der Rayleigh-Streuung ist proportional zur vierten Potenz der Frequenz f der elektromagnetischen Welle. Dies gilt nicht nur für unabhängig streuende Teilchen, d.h. bei Teilchenabständen größer als die Kohärenzlänge der Strahlung, sondern auch bei höherer Teilchenkonzentration für die Streuung an Inhomogenitäten des Brechungsindex durch eine statistische Anordnung der Teilchen, beispielsweise in Gasen oder Gläsern. Blaues Licht hat eine höhere Frequenz f als rotes und wird daher stärker gestreut. Dieser Effekt ist für das Himmelsblau am Tag sowie für die Morgenröte (und Abendröte) der Sonne am Horizont verantwortlich. Aus dem gleichen Grund erfolgt die Datenfernübertragung durch Glasfasern mit noch langwelligerem, infrarotem Licht.

Rayleigh-Streuung tritt auf, da das einfallende Licht die Elektronen eines Moleküls anregt und ein Dipolmoment ${\vec {p}}_{{\text{ind}}}=\alpha {\vec {E}}$ induziert, welches genauso schwingt wie die einfallende elektromagnetische Strahlung. Das induzierte Dipolmoment wirkt nun wie ein Hertzscher Dipol und sendet Licht aus, das dieselbe Wellenlänge wie das einfallende Licht besitzt.

Wirkungsquerschnitt

Der Wirkungsquerschnitt $\sigma$ der Rayleigh-Streuung für ein einzelnes Teilchen ergibt sich aus dem Oszillatormodell. Im Grenzfall niedriger Frequenzen (im Vergleich zur Eigenfrequenz, $\omega \ll \omega _{0}$ ) gilt:

$\sigma (\omega )\approx \sigma _{{\mathrm {Th}}}{\frac {\omega ^{4}}{\omega _{0}^{4}}}$

wobei $\sigma _{{\mathrm {Th}}}=0{,}665\cdot 10^{{-24}}\,{\mathrm {cm}}^{2}$ der Thomson-Wirkungsquerschnitt ist.

Für eine kleine Kugel mit Durchmesser d und Brechungsindex n ist die Intensität I im Abstand R des um den Winkel $\theta$ gestreuten Lichts

$I={\frac {I_{0}}{R^{2}}}{\frac {1+\cos ^{2}\theta }{2}}\left({\frac {2\pi }{\lambda }}\right)^{4}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6}\,.$

Dabei ist die einfallende Welle der Intensität $I_{0}$ unpolarisiert angenommen. Das Streulicht teilt sich im Verhältnis 1 : $\cos ^{2}\theta$ auf die Polarisationsrichtungen senkrecht und parallel zur Streuebene auf.

Das Blau beziehungsweise das Rot des Himmels

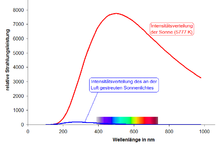
Leistungsverteilung von gestreutem Sonnenlicht

Die Rayleigh-Streuung erklärt, warum der Himmel blau erscheint. Die Wellenlänge von blauem Licht, $\lambda _{{\mathrm {blau}}}$ , beträgt rund 450 nm, die von rotem Licht rund 650 nm. Somit folgt für das Verhältnis der Wirkungsquerschnitte:

${\begin{aligned}{\frac {\sigma _{\text{blau}}}{\sigma _{\text{rot}}}}&={\frac {\frac {1}{\lambda _{\text{blau}}^{4}}}{\frac {1}{\lambda _{\text{rot}}^{4}}}}=\left({\frac {650\,{\text{nm}}}{450\,{\text{nm}}}}\right)^{4}\approx 4{,}5\end{aligned}}$

Im Bild ist die abgestrahlte Leistungsverteilung der Sonne, genähert durch das Plancksche Strahlungsgesetz aus einer Oberflächentemperatur von 5777 K, rot eingezeichnet. Das spektrale Maximum liegt danach bei grünem Licht (500 nm Wellenlänge). Das spektrale Maximum des Tageslichtes liegt hingegen u.a. aufgrund des hier beschriebenen Streueffektes bei 550 nm. Die Leistungsverteilung des Streulichtes (blaue Kurve) ergibt sich durch Multiplikation mit ω⁴. Demnach wandert das Maximum weit in den UV-Bereich. Tatsächlich liegt es aber im nahen UV, da bei kürzeren Wellenlängen molekulare Absorptionen hinzukommen.

Am Tag, wenn die Sonne hoch am Himmel steht, legt das Licht nur eine kurze Strecke durch die Atmosphäre zurück. Dabei wird nur wenig blaues Licht in andere Richtungen gestreut. Deshalb erscheint die Sonne gelb. Von hochfliegenden Flugzeugen aus erscheint die Sonne „weißer“, weil weniger blaue Lichtanteile weggestreut wurden.
Die Summe allen Streulichtes lässt den Himmel aus allen anderen Richtungen blau erscheinen. Auf dem Mond, wo eine dichte Atmosphäre fehlt, erscheint der Himmel dagegen auch tagsüber schwarz.
Bei niedrigem Sonnenstand ist die Strecke des Sonnenlichts durch die Erdatmosphäre viel länger. Dadurch wird ein Großteil der hochfrequenten Lichtanteile (blau) seitlich weggestreut, es bleibt überwiegend Licht mit langen Wellenlängen übrig und der Farbeindruck der Sonne verschiebt sich in Richtung rot. Dieser Effekt wird durch zusätzliche Partikel in der Luft (z.B. Dunst, Aerosole, Staub) weiter verstärkt. Für die Blaufärbung des Himmels im Zenit nach Sonnenuntergang ist allerdings die Chappuis-Absorption verantwortlich, die sich bei höherem Sonnenstand kaum bemerkbar macht.

Stärke der Lichtschwächung durch Rayleigh-Streuung

Um die Stärke der Rayleigh-Streuung quantitativ zu berechnen, ist zu berücksichtigen, dass innerhalb eines Kohärenzvolumens der Strahlung die von den Molekülen ausgehenden Elementarwellen interferieren, sodass nicht Intensitäten nach obiger Formel, sondern Streuamplituden addiert werden müssen. Die Teilchendichte, unterhalb derer dieser Effekt für Sonnenlicht vernachlässigt werden darf, beträgt etwa 1/μm³, sieben Größenordnungen unter dem für die Atmosphäre relevanten Wert. Die mittlere Dichte innerhalb eines streuenden Volumenelements ist für die Streuung irrelevant, wirksam sind die Dichteschwankungen.

Ein Ergebnis der Statistik ist, dass die Schwankungsamplitude der Teilchenzahl gem. der Poisson-Verteilung nur mit der Wurzel der Teilchenzahl zunimmt. Da kürzere Wellenlängen an feineren Strukturen aus entsprechend weniger Teilchen gestreut werden, 'sieht' diese Strahlung stärkere Schwankungsamplituden als längerwellige Strahlung. Bei fester Wellenlänge hängt die Schwankungsamplitude von der Wurzel der Teilchendichte des Gases ab. Die gestreute Intensität hängt aber quadratisch von der Schwankungsamplitude ab, also linear von der Dichte. Insgesamt gilt für die Lichtschwächung in der Atmosphäre bei senkrechtem Einfall nach Paetzold (1952):

$k={\frac {\,5\cdot 32\,\pi ^{{3}}\,(n_{0}-1)^{2}}{3\cdot \ln 100\cdot \lambda ^{4}}}\,{\frac {H}{N_{0}}}$

Darin ist die sogenannte Extinktion in astronomischen Größenklassen, $n_{{\mathrm {0}}}$ der Brechungsindex der Luft unter Normalbedingungen, die effektive Dicke der Atmosphäre (Skalenhöhe, siehe barometrische Höhenformel) und $N_{0}$ die Teilchendichte der Luft (erneut unter Normalbedingungen). Dass letztere im Nenner steht, ist nur ein scheinbarer Widerspruch zu dem oben Gesagten, denn der Term $n_{0}-1$ ist proportional zur Dichte und steht quadratisch im Zähler.

Aus der Extinktion folgt wiederum die Transmission , das Verhältnis zwischen von der streuenden Schicht durchgelassenen und einfallenden Intensität:

$T=10^{{-0{,}4\,k}}$

Das ist die in der Astronomie gebräuchliche Form des Lambert-Beerschen Gesetzes. In der Praxis wird auch

$T={\mathrm {e}}^{{-\tau }}$

benutzt, mit $\tau$ als optischer Tiefe. Es gilt die einfache Umrechnung:

$k=1{,}086\,\tau$

Transmission der klaren Atmosphäre auf Meereshöhe in Abhängigkeit von Wellenlänge und Einfallswinkel

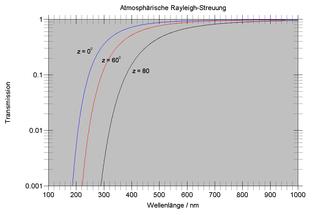
Bei schrägem Einfall unter einem Zenitwinkel ist die effektive Schichtdicke näherungsweise (bei planparalleler Schichtung):

$H(z)={\frac {H(0)}{\cos(z)}}$

Nach Paetzold (1952) ist $N_{0}=2{,}70\cdot 10^{{25}}~{\mathrm {m}}^{{-3}}$ sowie $H=7990~{\mathrm {m}}$ . Nach Stoecker (1997) ist $n_{0}=1{,}000292$ . Einsetzen liefert

$\tau ={\frac {0{,}0084~\mu {\mathrm {m}}^{4}}{\cos(z)\,\lambda ^{4}}}$

Im Visuellen (550 nm) passieren bei senkrechtem Einfall etwa 90 % des Lichts die Atmosphäre, im Blauen (440 nm) noch etwa 80 %. Bei flachem Einfall unter einem Zenitwinkel von 80° liegen diese Anteile nur noch bei 60 % und 25 %. Die bereits diskutierte Rötung des Lichts durch die Rayleigh-Streuung wird so klar verständlich.

In der Praxis ist die Lichtschwächung durch weitere Streuung an Aerosol- und Staubpartikeln (siehe Mie-Streuung) deutlich größer. Nach Naturkatastrophen wie Vulkanausbrüchen ist diese zusätzliche Extinktion besonders stark. So fanden Grothues und Gochermann (1992) nach dem Ausbruch des Pinatubo im Jahre 1991 auf La Silla (einer der Standorte des Europäischen Südobservatoriums (ESO)), bei senkrechtem Lichteinfall im Visuellen eine Lichtschwächung von 0,21 Größenklassen (normal sind 0,13 Größenklassen). Die Transmission war also von 89 % auf 82 % vermindert. Im Blauen war der Extinktionskoeffizient von 0,23 auf 0,31 Größenklassen angestiegen, d.h., die Transmission war von 81 % auf 75 % gefallen.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de