Figurierte Zahl

Figurierte Zahlen sind Klassen von Zahlen, die sich auf geometrische Figuren beziehen. Legt man regelmäßige Figuren aus Spielsteinen und zählt die Steine, erhält man figurierte Zahlen. Beispiele für figurierte Zahlen sind die Quadratzahlen, Kubikzahlen und Pyramidenzahlen.

Die Folgen von figurierten Zahlen bilden so genannte arithmetische Folgen. Zur Bestimmung der expliziten Formel untersucht man die Differenzen zwischen benachbarten Folgegliedern, die selber wiederum eine Folge, die Differenzenfolge, bilden. Ist keine andere Möglichkeit ersichtlich, so lässt sich die explizite Gesetzmäßigkeit jeder arithmetischen Folge mit dem sogenannten Polynomansatz algebraisch bestimmen.

Schon die griechischen Mathematiker beschäftigten sich mit figurierten Zahlen.

Polygonalzahlen

Je nach Aufbau unterscheidet man dezentrale und zentrierte Polygonalzahlen, wobei erstere meist nur Polygonalzahlen genannt werden. Der Begriff Polygonalzahl wird auch als Überbegriff für dezentrale und zentrierte Polygonalzahlen verwendet.

(Dezentrale) Polygonalzahlen

Siehe Hauptartikel: Polygonalzahl

Eine Polygonalzahl ist eine Zahl, zu der es ein Polygon (Vieleck) gibt, das sich mit einer entsprechenden Zahl an Steinen legen lässt. Beispielsweise ist die 16 eine Polygonalzahl, da sich ein Quadrat aus 16 Steinen legen lässt.

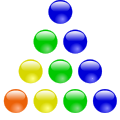Die 10 ist die vierte Dreieckszahl.
Die 16 ist die vierte Quadratzahl.
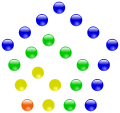Die 22 ist die vierte Fünfeckszahl.
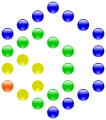Die 28 ist die vierte Sechseckszahl.

Es gibt für alle Primzahlen p > 5 eine n-te k-Polygonalzahl $P_{k}^{(2)}(n),n\geq 3,k\geq 3$ mit $p-1=P_{k}^{(2)}(n)$ , aber keine $p+1=P_{k}^{(2)}(n),n\geq 4,k\geq 3$ sowie zumindest ein $2\leq r<p-2,p-2=r{\pmod {P_{3}^{(2)}(r)}}$ mit der Dreieckszahl $P_{3}^{(2)}(r)$ . Für den größeren Primzahlzwilling p' > 5 gilt sogar ausschließlich $p'-2=2{\pmod {P_{3}^{(2)}(2)}}$ .

Zentrierte Polygonalzahlen

Ein weiteres Legemuster für regelmäßige Polygone beginnt mit einem Stein in der Mitte. Um diesen herum werden mehrere Polygone gelegt, wobei sich deren Seitenlängen von innen nach außen jeweils um eins erhöhen. Die dazu notwendige Anzahl an Steinen entspricht einer zentrierten Polygonalzahl. Die folgenden Bilder zeigen einige Beispiele:

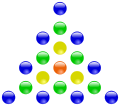Die 19 ist die vierte zentrierte Dreieckszahl.
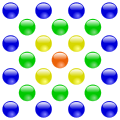Die 25 ist die vierte zentrierte Quadratzahl.
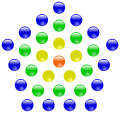Die 31 ist die vierte zentrierte Fünfeckszahl.
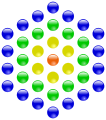Die 37 ist die vierte zentrierte Sechseckszahl.

Rechteckzahlen oder pronische Zahlen

Zwölf Kugeln bilden ein Rechteck.

Siehe Hauptartikel: Rechteckzahl

Eine Rechteckzahl oder pronische Zahl ist das Produkt zweier aufeinanderfolgender natürlicher Zahlen. Beispielsweise ist $12 = 3 \cdot 4$ eine Rechteckzahl. Legt man Steine zu einem Rechteck, dessen eine Seite um 1 länger ist als die zweite, so entspricht die Anzahl der Steine einer Rechteckszahl.

Dreidimensionale Körper

Die geometrischen Konstruktionen zu den Polygonalzahlen lassen sich von ebenen Figuren auf dreidimensionale Körper ausweiten. So entstehen Pyramidalzahlen und weitere Arten von figurierten Zahlen. Da es sich bei den Figuren um Polyeder handelt, verwenden manche Autoren hierfür den Begriff Polyederzahl.

Pyramidalzahlen oder Pyramidenzahlen

Siehe Hauptartikel: Pyramidenzahl

Addiert man die ersten Quadratzahlen erhält man die -te quadratische Pyramidalzahl Pyr_4(n) . Geometrisch bedeutet das, mehrere Quadrate zu einer Pyramide zu stapeln. Das folgende Bild zeigt dies für die vierte quadratische Pyramidalzahl.

Dieses Konstruktionsprinzip lässt sich von Quadratzahlen auf beliebige Polygonalzahlen übertragen. Dadurch entstehen die unterschiedlichen Klassen der Pyramidalzahlen.

Summen zentrierter Polygonalzahlen

Oktaederzahlen

Die Oktaederzahlen können als Summe der ersten zentrierten Quadratzahlen interpretiert werden:

$Okt_{n}=\sum _{i=1}^{n}ZQ_{i}=ZQ_{1}+ZQ_{2}+\ldots +ZQ_{n}=Pyr_{4}(n)+Pyr_{4}(n-1)=n+4T_{n-1}$

Die ersten Oktaederzahlen sind

0, 1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891, 1156, … (Folge A005900 in OEIS).

Kubikzahlen

Die (dezentralen) Kubikzahlen sind die Summe der ersten zentrierten Sechseckszahlen. Die direkte Berechnungsformel lautet:

$Kub_{n}=n^{3}$

Zentrierte Kubikzahlen

Zentrierte Kubikzahlen lassen sich analog definieren als

$ZK_{n}=Kub_{n}+Kub_{n-1}=n^{3}+(n-1)^{3}=2n^{3}-3n^{2}+3n-1$ .

Rhombische Dodekaederzahlen

Die rhombischen Dodekaederzahlen lassen sich zu einem Rhombendodekaeder zusammenbauen. Sie haben die Form

$ZK_{n}+6\cdot Pyr_{4}(n)=(2n-1)(2n^{2}-2n+1)$ .

Die ersten Zahlen dieser Form sind

0, 1, 15, 65, 175, 369, 671, … (Folge A005917 in OEIS).

Reguläre figurierte Zahlen

Figurierte Zahlen lassen sich für beliebige Dimensionen definieren. Allgemein ist die -te figurierte Zahl der Ordnung mit dem Binomialkoeffizienten

$f^n_r = {n + r - 1 \choose r} = \frac{(n + r - 1)(n + r - 2) \ldots n}{1 \cdot 2 \cdot \ldots \cdot r}$

identisch.

Mit steigender Ordnung entstehenden so aus den Dreieckszahlen

$f^n_2 = \Delta_n = 1 + 2 + \ldots + n$

die Tetraederzahlen

$f^n_3 = T_n = \Delta_1 + \Delta_2 + \ldots + \Delta_{n}$ ,

und Pentatopzahlen

$f^n_4 = P_n = T_1 + T_2 + \ldots + T_{n}$ ,

Diese Folge lässt sich in beliebige Dimensionen rekursiv fortsetzen:

$f^n_{r+1} = \sum_{i=1}^n f^i_r = f^1_r + f^2_r + \ldots + f^n_r$

Figurenzahlen, errichtet über den Seiten des pythagoräischen k-Dreiecks

Verallgemeinert errichtet der Satz des Pythagoras mit k=0 jeweils Quadrate mit der Fläche $n\cdot (n+0)=n^{2}$ (ganzzahlig die Quadratzahlen n²) über den Seiten eines pythagoräischen k-Dreiecks (zum Begriff siehe Folge A198453 in OEIS). Für bestimmte ganzzahlige pythagoräische k-Tripel (a,b,c) mit $a^{2}+b^{2}=c^{2}$ ist das Dreieck ABC nach dem Cosinussatz rechtwinklig und der Differenzwinkel $\phi$ zum rechten Winkel über der längsten Seite somit Null, wodurch $csc(\phi )=(a+b+c+0)/0=\infty$ den Grenzwert der natürlichen Zahlen annimmt (Unendlichkeitsaxiom).

Rechteckssatz (6,3,7)

Dreieckssatz (2,2,3)

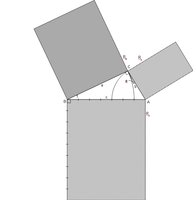
Im Fall $k=\pm 1$ werden rechtwinklige Dreiecke der Fläche $1/2\cdot n\cdot (n+1)=T(n)$ (ganzzahlig die Dreieckzahlen Δ_n) je mit der kleinen bzw. großen Kathete über den Seiten des Dreiecks ABC errichtet. Für bestimmte ganzzahlige pythagoräische $\pm 1$ -Tripel (a,b,c) mit $T(a)+T(b)=T(c)$ ist das Dreieck ABC zwar stumpf-/spitzwinklig, aber der $csc(\phi )=(a+b+c+1)/1$ des Differenzwinkels zum rechten Winkel über der längsten Seite ist ganzzahlig (Folge A012132 in OEIS).

Im Fall $k=\pm 2$ werden spezielle 2-Rechtecke der Fläche $n\cdot (n+2)=R(n)$ (ganzzahlig die 2-Rechteckszahlen R_n) je mit der kleinen bzw. großen Rechteckseite über den Seiten des Dreiecks ABC errichtet. Für bestimmte ganzzahlige pythagoräische $\pm 2$ -Tripel (a,b,c) mit $R(a)+R(b)=R(c)$ ist das Dreieck ABC mit geradzahligem Umfang zwar stumpf-/spitzwinklig, aber der $csc(\phi )=(a+b+c+2)/2$ des Differenzwinkels zum rechten Winkel über der längsten Seite ist ganzzahlig (Folge A198457 in OEIS).

In den Fällen $k=\pm 1$ oder $k=\pm 2$ liefert der Cosinussatz deshalb spezielle Aussagen zur Teilbarkeit. Allgemein konvergiert im Grenzübergang des Dreiecksumfangs a+b+c gegen Unendlich der Differenzwinkel $\phi$ gegen Null und somit die Form des pythagoräischen k-Dreiecks ABC zu einem (0-)pythagoräischen Dreieck ABC (Folge A103606 in OEIS).

Literatur

John H. Conway, Richard K. Guy: Zahlenzauber. Von natürlichen und imaginären und anderen Zahlen. Birkhäuser, Basel u.a. 1997, ISBN 3-7643-5244-2.
Lancelot Hogben: Mathematik für alle. Eine Einführung in die Wissenschaft der Zahlen und Figuren. Neu überarbeitete Ausgabe. Pawlak, Herrsching 1985, ISBN 3-88199-208-1.
Jochen Ziegenbalg: Figurierte Zahlen. Springer, 2018, ISBN 978-3-658-20934-6.

Basierend auf einem Artikel in:

Wikipedia.de