Additionsverfahren (Mathematik)
und 
folgt das Gleichungssystem 
.
Wenn nämlich beide Waagen im Vorfeld im Gleichgewicht waren, so ist dies die
Waage auch, wenn man die jeweiligen Seiten zusammenlegt.Das Additionsverfahren ist ein Verfahren, das zur Lösung von Gleichungssystemen genutzt werden kann. Der wahrscheinlich bekannteste Lösungsansatz zur Lösung von Gleichungssystemen, das Gaußsche Eliminationsverfahren, bedient sich des Additionsverfahrens, es ist aber auch allgemein bei der Lösung von Gleichungssystemen von Bedeutung.
Beim Additionsverfahren werden Gleichungen addiert. Dies geschieht in der Regel so, dass eine oder mehrere Variablen (Unbekannte) in den Gleichungen eliminiert werden.
Rechtfertigung (Anschaulich)
Als Beispiel soll folgendes lineare Gleichungssystem gelöst werden:
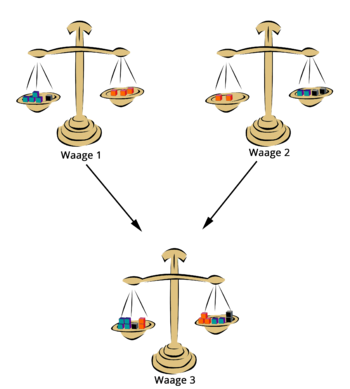
Man kann sich beide Gleichungen als ausgeglichene Waagen vorstellen. Waage 1
hat in der linken Schale 
und in der rechten 
liegen. Waage 2 hat in der linken Schale 
und in der rechten 
liegen.
Legt man die Inhalte der linken Schalen zusammen, müssen diese also so viel wiegen wie die rechten Schalen zusammen. Als Formel erhält man:
Sortiert man die linke Seite der Gleichung nach den Unbekannten, hebt sich
weg und man erhält eine Lösung für 
Auch das vorherige Vervielfachen einer Gleichung ändert nichts am
Gleichgewicht der jeweiligen Waage. Ein Mehrfachadditionsverfahren wie
oder ein Subtraktionsverfahren wie 
ist also lediglich eine abkürzende Schreibweise für eine Äquivalenzumformung
mit anschließendem Additionsverfahren. Für
wird die zweite Gleichung zunächst verdreifacht und dann beide Gleichungen
addiert (ein ausführliches Beispiel dazu steht unten). Für
wird die zweite Gleichung zunächst auf beiden Seiten mit 
multipliziert und dann beide Gleichungen addiert.
Beispiel
Mit Hilfe des Additionsverfahrens soll das folgende Gleichungssystem gelöst werden:
Dazu muss eine der beiden Gleichungen so umgeformt
werden, dass bei einer Addition der beiden Gleichungen eine Variable
verschwindet. In diesem Beispiel multiplizieren wir dazu Gleichung (2) auf
beiden Seiten mit 
.
Dadurch erhalten wir ein gleichwertiges Gleichungssystem, in dem der Term
vorkommt.
Nun werden beide Gleichungen des Systems addiert und somit in einer Gleichung zusammengefasst:
Anschließend löst man nach der verbliebenen Variablen
auf:
Damit ist der Wert der ersten Variable bekannt. Diesen Wert (
)
setzen wir in Gleichung (1) ein, um den Wert der zweiten Variable zu berechnen.
Dadurch erhalten wir den Wert für die zweite Variable. Die Lösung des
Gleichungssystems gibt man als Lösungsmenge
an, also 
.
Siehe auch
Wikipedia.de
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.07. 2021