Gradfolge

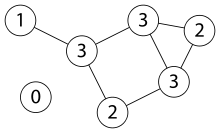
Graph mit eingezeichneten Knotengraden und der Gradfolge 0,1,2,2,3,3,3

Als Gradfolge (oder auch Valenzsequenz bzw. Gradsequenz) eines einfachen Graphen bezeichnet man in der Graphentheorie die aufsteigende Folge der Knotengrade aller Knoten eines Graphen.

Definition

Die Gradfolge eines einfachen Graphen G = (V, E) mit den Knoten $v_{1},v_{2},\ldots ,v_{n}\in V$ und Knotengraden $d(v_{1})\leq d(v_{2})\leq \dots \leq d(v_{n})$ ist die Folge natürlicher Zahlen

$d_{1},d_{2},\ldots ,d_{n}$ ,

wobei $d_{i}=d(v_{i})$ für alle $i=1,2,\dots ,n$ jeweils den Grad des Knotens $v_{i}$ angibt. Eine aufsteigende Folge natürlicher Zahlen heißt graphisch, wenn mindestens ein einfacher Graph existiert, der diese Gradfolge aufweist.

Beispiele

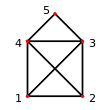
Haus vom Nikolaus mit Knotennummerierung

Gradfolge

Das Haus vom Nikolaus hat mit der Knotennummerierung im nebenstehenden Bild die Knotengrade $d(1)=d(2)=3,d(3)=d(4)=4$ und $d(5)=2$ . Eine Sortierung nach dem Grad ergibt dann die zugehörige Gradfolge $2,3,3,4,4$ .

Graphische Folgen

Die Folge $0,1,2,2,3,3,3$ ist graphisch, da der eingangs gezeigte Graph genau diese Grade hat. Die Folge $1,3,4$ ist aber beispielsweise nicht graphisch, da kein einfacher Graph mit drei Ecken existieren kann, der einen Knoten mit Grad vier hat.

Verwendung

Gradfolgen werden in der Graphentheorie beim Hamiltonkreisproblem betrachtet, insbesondere bei einem Satz von Vašek Chvátal, der Aussagen über die Existenz von Hamiltonkreisen durch die Betrachtung von Gradfolgen folgert.

Literatur

Reinhard Diestel: Graphentheorie. Springer, Berlin 2010, ISBN 978-3-642-14911-5.

Basierend auf einem Artikel in:

Wikipedia.de