Linearer Raum (Geometrie)
Ein linearer Raum, manchmal auch als Inzidenzraum bezeichnet,
ist eine grundlegende Struktur in der endlichen
Geometrie. Als eigenständiger Begriff wurde er 1964 von Paul Libois eingeführt. Außer in Trivialfällen (bei höchstens eindimensionalen
Räumen) kann man lineare Räume als Verallgemeinerung der schwach affinen
Räume ansehen, die wiederum eine Verallgemeinerung der affinen Räume sind.
Gleichzeitig stellen lineare Räume auch eine Verallgemeinerung der mindestens
zweidimensionalen projektiven
Räume dar. Endliche lineare Räume wiederum können als Verallgemeinerung von
2-
Blockplänen angesehen werden, bei der man darauf verzichtet, dass auf jeder
Geraden (=Block) die gleiche Anzahl von Punkten liegt.
Definitionen
Linearer Raum
Sei
eine I-Inzidenzstruktur,
bei der man die Elemente von
als Punkte und die Elemente von
als Geraden (oder Blöcke) bezeichnet. Weiterhin verwendet man für
die Inzidenzrelation auch die Sprechweisen ein Punkt
liegt auf einer Geraden
(
mit
)
und eine Gerade
geht durch einen Punkt
(
mit
).
Die Inzidenzstruktur
wird als linearer Raum bezeichnet, wenn die folgenden 3 Axiome erfüllt
sind:
- (L1) Durch 2 Punkte geht genau eine Gerade.
- (L2) Auf jeder Geraden liegen mindestens 2 Punkte.
- (L3) L besitzt mindestens 2 Geraden.
Gelegentlich wird das Axiom L3 in der Literatur nicht gefordert, in einem solchen Fall bezeichnet man diejenigen linearen Räume die es dennoch erfüllen als nicht triviale lineare Räume. Besitzt der lineare Raum eine endliche Anzahl von Punkten, so spricht man auch kurz von einem endlichen linearen Raum.
Es werden fast immer nur endliche lineare Räume untersucht. Wie bei Blockplänen
wird dann die Anzahl der Punkte in der Regel mit ,
die Anzahl der Geraden mit
bezeichnet.
Partieller linearer Raum
Gelten für eine Inzidenzstruktur die Axiome (L2) und (L3), aber an Stelle von (L1) nur das schwächere Axiom
- (L1p) „Durch 2 Punkte geht höchstens eine Gerade.“,
so spricht man von einem partiellen linearen Raum (eng. partial linear space).
Entarteter linearer Raum, near-pencil
- Einen linearen Raum mit
Punkten, der eine Gerade mit
Punkten besitzt, bezeichnet man als degenerierten linearen Raum (degenerate linear space oder near-pencil). Alle anderen linearen Räume bezeichnet man als nichtdegenerierte lineare Räume.
- Die Klasse der projektiven Ebenen wird mit der Klasse der degenerierten linearen Räume zusammengefasst zur Klasse der verallgemeinerten projektive Ebene.
Eigenschaften
- Jeder lineare Raum ist eine einfache Inzidenzstruktur, das heißt, eine Gerade ist durch die mit ihr inzidierenden Punkte eindeutig bestimmt, kann also als Menge ihrer Punkte aufgefasst werden.
- Für endliche lineare Räume ist die Anzahl
der Geraden nie kleiner als die Anzahl
der Punkte, es gilt also stets
. Das ist die Aussage eines Satzes von de Brujin und Erdős.
-
- Gleichheit
gilt genau dann, wenn der lineare Raum eine verallgemeinerte projektive Ebene ist, also entweder eine projektive Ebene oder ein near-pencil.
- Die maximal mögliche Anzahl an Geraden bei gegebener Punktzahl
ist
. Der lineare Raum ist dann der vollständige Graph auf v Knoten.
- Gleichheit
Beispiele
- Die normale euklidische Ebene bildet einen unendlichen linearen Raum.
- Etwas allgemeiner sind alle affinen und projektiven Räume, deren Dimension größer oder gleich 2 ist, und damit insbesondere auch projektive Ebenen, etwa die Fano-Ebene, (nicht triviale) lineare Räume.
- Eine punktierte projektive Ebene entsteht aus einer projektiven Ebene durch Weglassen genau eines Punktes: Eine solche Ebene bildet stets einen linearen Raum.
- Eine affine Ebene mit einem Fernpunkt entsteht aus einer affinen Ebene durch Hinzufügen genau eines Fernpunktes als Schnittpunkt genau einer fest gewählten Parallelenschar der Ebene. Auch diese Ebenen bilden stets einen linearen Raum.
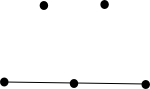
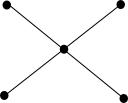
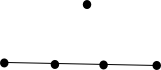
Im Folgenden sind alle vier linearen Räume mit fünf Punkten ()
aufgelistet. Hierbei ist es üblich, in der graphischen Darstellung alle Geraden
mit nur zwei Punkten aus Gründen der Übersicht nicht zu zeichnen.
|
|
|
|
|
| 10 Geraden: Vollständiger Graph auf 5 Knoten. | 8 Geraden | 6 Geraden: die affine Ebene |
5 Geraden: der near-pencil mit 5 Punkten. |
|
|
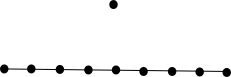
| near pencil mit 10 Punkten (10 Geraden) |


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.10. 2019