Machscher Kegel

Machscher Kegel. Im Fall v>v_s bildet sich eine Stoßwelle (blau dargestellt). v_s bezeichnet hier die Schallgeschwindigkeit.

Schlierenfoto eines Projektiles bei Mach 1,2 im Windkanal. Sichtbar sind schräge Verdichtungsstöße und Verdünnungsfächer, die durch die Umlenkung des Fluids entstehen. Sie unterscheiden sich im Winkel vom Machschen Kegel.

Ein Jagdbomber F/A-18 Hornet im Überschallflug mit Wolkenscheibeneffekt

Der Machsche Kegel ist eine Stoßwelle, die bei Wellen im Zusammenhang mit hohen Geschwindigkeiten auftritt. Er wurde nach Ernst Mach benannt.

Ein sich mit der Geschwindigkeit bewegendes Objekt verdichtet das Medium vor sich her, hiervon ausgelöste Schallwellen breiten sich mit Schallgeschwindigkeit $c_{{{\mathrm S}}}$ kugelförmig aus. Bewegt sich jedoch das Objekt selbst mit Überschallgeschwindigkeit, also schneller als die Ausbreitungsgeschwindigkeit der Wellen, dann kann sich in Bewegungsrichtung des Objektes die Verdichtungsfront niemals vom Objekt ablösen und läuft damit permanent diesem voran. Die ausgelösten Stoßwellen formen sich, wie die Überlagerung von Elementarwellen nach dem Huygensschen Prinzip zeigt, zu einem im Bezugssystem des bewegten Objektes stationären Kegelmantel. Der halbe Spitzenwinkel dieses Kegels heißt Machscher Winkel.

Sichtbarer Machscher Kegel

Bei hoher Luftfeuchtigkeit wird die Stoßfront des Machschen Kegels als Wolkenscheibe sichtbar. Im Kegel folgt unmittelbar nach der Kompression ein ähnlich starker Unterdruck. Durch diese adiabatische Expansion überschreitet der Partialdruck des Wassers den Sättigungsdampfdruck deutlich. Als Folge kondensiert Wasserdampf zu kleinen Tröpfchen, die als Nebelwand sichtbar sind. Hinter der Stoßfront normalisiert sich der Luftdruck, die Tröpfchen verdampfen und der Nebel löst sich auf. Es entsteht der Eindruck einer am Flugzeug befestigten Wolkenscheibe.

Mit Schlierenoptik können Machsche Kegel im Windkanal dargestellt und vermessen werden.

Mathematische Beschreibung

Öffnungswinkel des Machschen Kegels

Die Gleichung für den halben Öffnungswinkel des Machschen Kegels lautet:

$\sin \varphi ={\frac {s_{{\text{Welle}}}}{s_{{\text{Objekt}}}}}={\frac {c_{{{\mathrm S}}}\cdot t}{v\cdot t}}={\frac {c_{{{\mathrm S}}}}{v}}={\frac {1}{{\mathit {Ma}}}}\,$

: in der Zeit zurückgelegter Weg
$\varphi$ : machscher Winkel
$c_{{{\mathrm S}}}$ : Schallgeschwindigkeit
: Fluggeschwindigkeit des Objekts
${\mathit {Ma}}$ : Mach-Zahl

Bei Schallgeschwindigkeit hat der Kegelöffnungswinkel eine Größe von 180°. Der Kegel hat in diesem Fall die Form einer ebenen Stoßfront angenommen. Für $v>c_{\mathrm {S} }$ bilden die sich durchdringenden Kugelwellenfronten Kegel mit konstruktiver Interferenz.

Beschreibung von dynamischen Wellenbildern

$c_{s}$ : Schallgeschwindigkeit
$f_{s}$ : Frequenz der Schallquelle
$\omega_s$ : Kreisfrequenz der Schallquelle
$\lambda$ : Wellenlänge
$v_{x},v_{y}$ : Geschwindigkeit des Flugzeugs
: Wellenpropagationskonstante
$\varphi$ : Azimutaler Winkel (Polarkoordinaten)

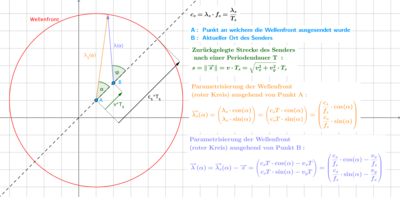
Beschreibung der Wellenfront als verschobene Kreisparametrisierung:

Graphische Darstellung des Wellenlängenvektors

${\overrightarrow {\lambda }}(\alpha )={\begin{pmatrix}\lambda _{x}(\alpha )\\\lambda _{y}(\alpha )\end{pmatrix}}={\begin{pmatrix}{\frac {c_{s}}{f_{s}}}\cos(\alpha )-{\frac {v_{x}}{f_{s}}}\\{\frac {c_{s}}{f_{s}}}\sin(\alpha )-{\frac {v_{y}}{f_{s}}}\end{pmatrix}}\quad \quad \alpha \in [-\pi ,\pi ]$

Hierbei entspricht $\alpha$ einem freien Parameter welcher sich im Intervall $[-\pi ,\pi ]$ befindet, ist jedoch nicht gleich dem typischen azimutalen Umlaufwinkel der Polarkoordinaten. Die geometrische Herleitung ist in der Abbildung „Graphische Darstellung des Wellenlängenvektors“ zu sehen.

Die winkelabhängige Wellenlänge ist die Norm dieser Kreisparametrisierung:

$\lambda (\alpha )=\|{\overrightarrow {\lambda }}(\alpha )\|={\sqrt {\lambda _{x}^{2}(\alpha )+\lambda _{y}^{2}(\alpha )}}$

Die Wellenpropagationskonstante lässt sich damit wie folgt angeben:

$k(\alpha )={\frac {2\pi }{\lambda (\alpha )}}$

Der azimutale Umlaufwinkel wird in Abhängigkeit von $\alpha$ aus den Komponenten des Wellenlängenvektors berechnet werden:

$\tan(\varphi (\alpha ))={\frac {\lambda _{y}(\alpha )}{\lambda _{x}(\alpha )}}\quad \rightarrow \quad \varphi (\alpha )=\arctan 2(\lambda _{y}(\alpha ),\lambda _{x}(\alpha )),\quad -\pi \leq \alpha \leq \pi$

Eine effektive Umrechnung des azimutalen Winkels $\varphi$ in den Parameterwinkel $\alpha$ ist gegeben durch die folgende Formel in Determinanten-Schreibweise:

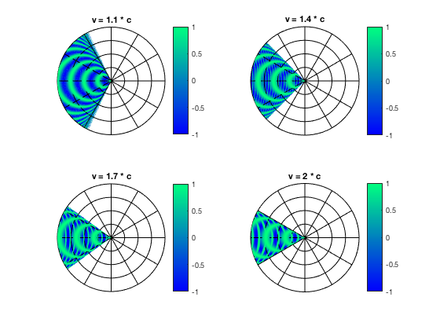$\alpha (\varphi )=\varphi -{\text{arcsin}}\left({\frac {1}{c_{s}}}\cdot {\begin{vmatrix}v_{x}&\cos \varphi \\v_{y}&\sin \varphi \end{vmatrix}}\right)\quad ,\quad -\infty <\varphi <\infty$

Einige Wellenbilder mit verschiedenen Machzahlen

Die Wellengleichung lässt sich damit als parametrisierte Fläche folgendermaßen beschreiben:

${\overrightarrow {u}}(r,\varphi ,t)={\begin{pmatrix}x(r,\varphi ,t)\\y(r,\varphi ,t)\\z(r,\varphi ,t)\end{pmatrix}}={\begin{pmatrix}r\cdot \cos \varphi \\r\cdot \sin \varphi \\A\cdot \cos(\omega _{s}t-k(\alpha (\varphi ))\cdot r)\end{pmatrix}}$

Der Parameter entspricht dem radialen Parameter der Polarkoordinaten. Die weiter oben zu sehende Animation ist nach diesem Berechnungsprinzip erstellt. Bei einer Mach-Zahl von 2 ist der Öffnungswinkel des Kegels exakt 30°.

Machscher Kegel

Sichtbarer Machscher Kegel

Mathematische Beschreibung

Öffnungswinkel des Machschen Kegels

Beschreibung von dynamischen Wellenbildern

Siehe auch