Normalisierung (Datenbank)

Unter Normalisierung eines relationalen Datenschemas (Tabellenstruktur) versteht man die Aufteilung von Attributen (Tabellenspalten) in mehrere Relationen (Tabellen) gemäß den Normalisierungsregeln (s.u.), so dass eine Form entsteht, die keine Redundanzen mehr enthält.

Ein konzeptionelles Schema, das Datenredundanzen enthält, kann dazu führen, dass bei Änderungen der damit realisierten Datenbank die mehrfach enthaltenen Daten nicht konsistent, sondern nur teilweise und unvollständig geändert werden, womit sie obsolet oder widersprüchlich werden können. Man spricht von auftretenden Anomalien. Zudem belegt mehrfache Speicherung derselben Daten unnötig Speicherplatz. Um Redundanz zu verhindern, normalisiert man solche Tabellen.

Es gibt verschiedene Ausmaße, in denen ein Datenbankschema gegen Anomalien gefeit sein kann. Je nachdem spricht man davon, dass es in erster, zweiter, dritter usw. Normalform vorliege. Diese Normalformen sind durch bestimmte formale Anforderungen an das Schema definiert.

Man bringt ein relationales Datenschema in eine Normalform, indem man fortschreitend anhand für sie geltender funktionaler Abhängigkeiten seine Relationen in einfachere zerlegt, bis keine weitere Zerlegung mehr möglich ist. Dabei dürfen jedoch auf keinen Fall Daten verloren gehen. Mit dem Satz von Delobel kann man für einen Zerlegungsschritt formal nachweisen, dass er keine Datenverluste mit sich bringt.

Normalisiert wird vor allem in der Phase des Entwurfs einer relationalen Datenbank. Für die Normalisierung gibt es Algorithmen (Synthesealgorithmus (3NF), Zerlegungsalgorithmus (BCNF) usw.), die automatisiert werden können.

Die Zerlegungsmethodik folgt der relationalen Entwurfstheorie.

Vorgehen

Ziel: Konsistenzerhöhung durch Redundanzvermeidung

Aufspaltung der Tabelle TBL_AdressenAlles

Bei der Normalisierung in diesen Bereichen werden zunächst Spalten (synonyme Begriffe: Felder, Attribute) von Tabellen innerhalb dieser Bereiche (der Datenschemata) in neue Spalten aufgeteilt, z.B. Adressen in Postleitzahl, Ort und Strasse. Anschließend werden Tabellen aufgeteilt, zum Beispiel eine Tabelle
tbl_AdressenAlles mit den Feldern Firma, Strasse, PLZ und Ort in diese Tabellen:

tbl_Adressen mit den Feldern AdressID, Firma, Strasse und PLZ
tbl_PLZOrt mit den Feldern PLZ und Ort

Siehe Bild Aufspaltung der Tabelle tbl_AdressenAlles – wobei die Tabelle tbl_Adressen noch den eindeutigen Primärschlüssel AdressID erhält.

Hinweis: In diesem Beispiel wird angenommen, dass es zu jeder Postleitzahl nur jeweils einen Ortsnamen gibt, was in Deutschland jedoch sehr oft nicht zutrifft – bspw. in ländlichen Gebieten, wo sich mitunter bis zu 100 Orte eine Postleitzahl „teilen“.

Die Normalisierung hat den Zweck, Redundanzen (mehrfaches Festhalten des gleichen Sachverhalts) zu verringern und dadurch verursachte Anomalien (z.B. infolge Änderung an nicht allen Stellen) zu verhindern, um so die Aktualisierung einer Datenbank zu vereinfachen (Änderungen lediglich an einer Stelle) sowie die Konsistenz der Daten zu gewährleisten.

Beispiel

Ein Beispiel dazu: Eine Datenbank enthält Kunden und deren Adressen sowie Aufträge, die den Kunden zugeordnet sind. Da es mehrere Aufträge vom selben Kunden geben kann, würde eine Erfassung der Kundendaten (womöglich mit Adressdaten) in der Auftragstabelle dazu führen, dass sie dort mehrfach vorkommen, obwohl der Kunde immer nur einen Satz gültiger Daten hat (Redundanz). Beispielsweise kann es dazu kommen, dass in einem Auftrag fehlerhafte Adressdaten zum Kunden eingegeben werden, im nächsten Auftrag werden die korrekten Daten erfasst. So kann es – in dieser Tabelle oder auch gegenüber anderen Tabellen – zu widersprüchlichen Daten kommen. Die Daten wären dann nicht konsistent, man wüsste nicht, welche Daten korrekt sind. Womöglich sind sogar beide Adressen nicht korrekt, weil der Kunde umgezogen ist (Lösung siehe unten).

Bei einer normalisierten Datenbank gibt es für die Kundendaten nur einen einzigen Eintrag in der Kundentabelle, mit der jeder Auftrag dieses Kunden verknüpft wird (üblicherweise über die Kundennummer). Im Falle des Umzugs eines Kunden (ein anderes Beispiel ist die Änderung der Mehrwertsteuer) gäbe es zwar mehrere Einträge in der entsprechenden Tabelle, die aber zusätzlich durch die Angabe eines Gültigkeitszeitraums unterscheidbar sind und im obigen Kundenbeispiel über die Kombination Auftragsdatum/Kundennummer eindeutig angesprochen werden können.

Ein weiterer Vorteil von Redundanzfreiheit, der bei Millionen Datensätzen einer Datenbank auch heute noch eine wichtige Rolle spielt, ist der geringere Speicherbedarf, wenn der Datensatz einer Tabelle zum Beispiel tbl_Auftrag auf einen Datensatz einer anderen Tabelle z.B. tbl_Kunde verweist, anstatt diese Daten selbst zu enthalten.

Aufspaltung von Tabellen zur Normalisierung

Dieses sind die Empfehlungen, die ausgehend von der Theorie der Normalisierung bei der Datenbankentwicklung gegeben werden, um vor allem Konsistenz der Daten und eine eindeutige Selektion von Daten zu gewährleisten. Die hierzu angestrebte Redundanzfreiheit steht allerdings in speziellen Anwendungsfällen in Konkurrenz zur Verarbeitungsgeschwindigkeit oder zu anderen Zielen. Es kann daher sinnvoll sein, auf eine Normalisierung zu verzichten oder diese durch eine Denormalisierung rückgängig zu machen, um

die Verarbeitungsgeschwindigkeit (Performance) zu erhöhen oder
Anfragen zu vereinfachen und damit die Fehleranfälligkeit zu verringern oder
Besonderheiten von Prozessen (zum Beispiel Geschäftsprozessen) abzubilden.

In diesen Fällen sollten regelmäßig automatische Abgleichroutinen implementiert werden, um Inkonsistenzen zu vermeiden. Alternativ können die betreffenden Daten auch für Änderungen gesperrt werden.

Normalformen

Zurzeit gebräuchliche Normalformen sind:

1. Normalform (1NF)
2. Normalform (2NF)
3. Normalform (3NF)
Boyce-Codd-Normalform (BCNF)
4. Normalform (4NF)
5. Normalform (5NF)

Zum einen dienen sie der Beurteilung der Qualität eines betrachteten Datenbankschemas, zum anderen helfen sie, Fehler beim Erzeugen neuer Schemata zu vermeiden.

Außerdem können mit Hilfe der Normalisierung Datenstrukturen aus nichtrelationalen Quellen gewonnen werden, die im Sinne des Normalisierungskonzepts formal korrekt sind und die Daten aus ihren jeweiligen nichtrelationalen Quellen, aus denen sie entstanden sind (zum Beispiel Formulardaten oder Spreadsheets), aufnehmen können.

Nachfolgend werden die Kriterien der jeweiligen Normalformen erklärt. Dabei ist zu beachten, dass jede Normalform die Kriterien der vorhergehenden Normalformen mit einschließt, d.h. für die folgenden Kriterienmengen gilt: ${\text{1NF}}\subseteq {\text{2NF}}\subseteq {\text{3NF}}\subseteq {\text{BCNF}}\subseteq {\text{4NF}}\subseteq {\text{5NF}}$ .

Erste Normalform (1NF)

Erläuterung

Jedes Attribut der Relation muss einen atomaren Wertebereich haben, und die Relation muss frei von Wiederholungsgruppen sein. (Anm.: statt „atomar“ wird auch die Bezeichnung „atomisch“ verwendet.)

Atomar heißt, dass zusammengesetzte, mengenwertige oder geschachtelte Wertebereiche (also relationenwertige Attributwertebereiche) nicht erlaubt sind. Der Wertebereich keines Attributs einer Relation in 1NF kann in weitere (sinnvolle) Teilbereiche aufgespaltet werden.

Beispiel: Die Adresse darf nicht als einzelnes Attribut verwendet werden, sondern muss – sofern es der zugrunde liegende Prozess erfordert – in PLZ, Ort, Straße, Hausnummer etc. aufgeteilt werden.

Frei von Wiederholungsgruppen bedeutet, dass Attribute, die gleiche oder gleichartige Information enthalten, in eine andere Relation ausgelagert werden müssen.

Ein Beispiel für eine Wiederholungsgruppe wäre eine Spalte { Telefon }, die mehrere Telefonnummern enthält oder auch eine Spaltengruppe { Telefon1, Telefon2, Telefon3 }, wobei im letzteren Fall anzumerken ist, dass es sich dabei nicht notwendigerweise um eine Wiederholungsgruppe handeln muss (siehe Alternative Formulierungen).

Praktischer Nutzen

Abfragen der Datenbank werden durch die 1NF erleichtert bzw. überhaupt erst ermöglicht, wenn die Attributwertebereiche atomar sind. So ist es beispielsweise in einem Feld, das einen ganzen Namensstring aus Titel, Vorname und Nachname enthält, schwierig bis unmöglich, nach Nachnamen zu sortieren.

Alternative Formulierungen

Alle Attribute enthalten atomare Inhalte, und die Relation hat eine feste Breite. Diese Formulierung bezieht sich darauf, dass es niemals nötig sein darf, weitere Attribute in die Relation aufzunehmen, weil die Wiederholungszahl der Wiederholungsgruppe zu klein wird (z.B.: es wird bei drei Attributen Telefon1–3 eine 4. Telefonnummer für eine Person bekannt). Sie ist insofern interessant, als sie helfen kann zu entscheiden, ob tatsächlich eine Wiederholungsgruppe vorliegt: Obwohl z.B. { .., Telefon1, Telefon2, Telefon3,.. } sehr stark das Vorhandensein einer Wiederholungsgruppe impliziert, könnte es bei lediglich anderen Attributnamen klar werden, dass – freilich unter dem Licht der Anwendung – dem nicht so sein muss: { .., Telefon, Fax, Mobil,.. }

Eine weitere Variante entsteht durch folgenden Zusatz: .. und die Relation einen Primärschlüssel hat. Obwohl diese Formulierung so nicht bei Edgar F. Codd nachgelesen werden kann, handelt es sich um eine Erweiterung, die zu ausgesprochen praxistauglichen Datenstrukturen führt.

Negativbeispiel: 1NF verletzt

CD_Lied
CD_ID	Album	Gründungsjahr	Erscheinungsjahr	Titelliste
4711	Anastacia – Not That Kind	1999	2000	{1. Not That Kind, 2. I’m Outta Love, 3. Cowboys & Kisses}
4712	Pink Floyd – Wish You Were Here	1965	1975	{1. Shine On You Crazy Diamond}
4713	Anastacia – Freak of Nature	1999	2001	{1. Paid my Dues}

Das Feld Album enthält die Attributwertebereiche Interpret und Albumtitel.
Das Feld Titelliste enthält eine Menge von Titeln.

Dadurch hat man ohne Aufspaltung folgende Probleme bei Abfragen:

Zur Sortierung nach Albumtitel muss das Feld Album in Interpret und Albumtitel aufgeteilt werden.
Die Titel können (mit einfachen Mitteln) nur alle gleichzeitig als Titelliste oder gar nicht dargestellt werden.

Lösung

CD_Lied
CD_ID	Albumtitel	Interpret	Gründungsjahr	Erscheinungsjahr	Track	Titel
4711	Not That Kind	Anastacia	1999	2000	1	Not That Kind
4711	Not That Kind	Anastacia	1999	2000	2	I’m Outta Love
4711	Not That Kind	Anastacia	1999	2000	3	Cowboys & Kisses
4712	Wish You Were Here	Pink Floyd	1965	1975	1	Shine On You Crazy Diamond
4713	Freak of Nature	Anastacia	1999	2001	1	Paid my Dues

Die Attributwertebereiche werden in atomare Attributwertebereiche aufgespalten:

Das Feld Album wird in die Felder Albumtitel und Interpret gespalten.
Das Feld Titelliste wird in die Felder Track und Titel gespalten sowie auf mehrere Datensätze aufgeteilt.

Da jetzt jeder Attributwertebereich atomar ist sowie die Tabelle einen eindeutigen Primärschlüssel (Verbundschlüssel aus den Spalten CD_ID und Track) besitzt, befindet sich die Relation in 1NF.

Zweite Normalform (2NF)

Erläuterung

Eine Relation ist genau dann in der zweiten Normalform, wenn die erste Normalform vorliegt und kein Nichtprimärattribut (Attribut, das nicht Teil eines Schlüsselkandidaten ist) funktional von einer echten Teilmenge eines Schlüsselkandidaten abhängt.

Anders gesagt: Jedes nicht-primäre Attribut (nicht Teil eines Schlüssels) ist jeweils von allen ganzen Schlüsseln abhängig, nicht nur von einem Teil eines Schlüssels. Wichtig ist hierbei, dass die Nichtschlüsselattribute wirklich von allen Schlüsseln vollständig abhängen.

Somit gilt, dass Relationen in der 1NF, deren Schlüsselkandidat(en) nicht zusammengesetzt sind, sondern lediglich aus jeweils (einem) einzelnen Attribut(en) bestehen, automatisch die 2NF erfüllen.

In einer Relation R(A,B) ist das Attribut B von dem Attribut A funktional abhängig, falls zu jedem Wert des Attributs A genau ein Wert des Attributs B gehört. In einer Relation R(S1,S2,B) ist das Attribut B von den Schlüsselattributen S1 und S2 voll funktional abhängig, wenn B von den zusammengesetzten Attributen (S1,S2) funktional abhängig ist, nicht aber von einem einzelnen Attribut S1 oder S2.

Diese informelle Definition kann wie folgt präzisiert werden:

Eine Relation ist genau dann in zweiter Normalform, wenn sie

in der ersten Normalform ist und
für jedes Attribut der Relation gilt:
- ist Teil eines Schlüsselkandidaten oder
- ist von einem Schlüsselkandidaten abhängig, aber
- ist nicht von einer echten Teilmenge eines Schlüsselkandidaten abhängig.

ist voll funktional abhängig von jedem Schlüsselkandidaten (wobei die Schlüsselkandidaten KC auch durch die Kombination mehrerer Attribute gebildet werden können). Die 2NF eliminiert alle partiellen funktionalen Abhängigkeiten, d.h. kein Nichtschlüsselattribut ist funktional abhängig von Teilen des Schlüsselkandidaten.

Falls ein Schlüsselkandidat zwei Attribute besitzt, können bei der Zerlegung in die 2NF höchstens drei Relationen entstehen. Falls ein Schlüsselkandidat drei Attribute besitzt, können bei der Zerlegung in die 2NF höchstens sieben Relationen entstehen. Das sind jeweils die Anzahl der Teilmengen einer gegebenen Menge minus 1 (leere Menge) und entspricht der Anzahl der Elemente der Potenzmenge ( $2^{n}$ ) als Obergrenze.

Praktischer Nutzen

Die 2NF erzwingt wesentlich „monothematische“ Relationen im Schema: jede Relation modelliert nur einen Sachverhalt.

Dadurch werden Redundanz und die damit einhergehende Gefahr von Inkonsistenzen reduziert. Nur noch logisch/sachlich zusammengehörige Informationen finden sich in einer Relation. Dadurch fällt das Verständnis der Datenstrukturen leichter.

Negativbeispiel: 2NF verletzt

CD_Lied
CD_ID	Albumtitel	Interpret	Gründungsjahr	Erscheinungsjahr	Track	Titel
4711	Not That Kind	Anastacia	1999	2000	1	Not That Kind
4711	Not That Kind	Anastacia	1999	2000	2	I’m Outta Love
4711	Not That Kind	Anastacia	1999	2000	3	Cowboys & Kisses
4712	Wish You Were Here	Pink Floyd	1965	1975	1	Shine On You Crazy Diamond
4713	Freak of Nature	Anastacia	1999	2001	1	Paid my Dues

Der Primärschlüssel der Relation ist aus den Feldern CD_ID und Track zusammengesetzt. (Grundsätzlich darf ein Primärschlüssel aus mehreren Attributen bestehen, jedoch entsteht daraus im genannten Beispiel ein Konflikt.)
Die Felder Albumtitel, Interpret und Erscheinungsjahr sind vom Feld CD_ID abhängig, aber nicht vom Feld Track. Dieser (Punkt 2) verletzt die 2. Normalform, da die drei nicht-primären Attribute nicht nur von einem Teil des Schlüssels (hier CD_ID) abhängen dürfen. Wäre der Schlüssel nicht zusammengesetzt (siehe Punkt 1), so könnte dies nicht passieren.

Probleme, die sich daraus ergeben

Die Informationen aus diesen drei Feldern sind, wie am Beispiel der CD Not That Kind zu erkennen, mehrfach vorhanden, d.h. redundant. Dadurch besteht die Gefahr, dass die Integrität der Daten verletzt wird. So könnte man den Albumtitel für das Lied Not That Kind in I Don’t Mind ändern, ohne jedoch die entsprechenden Einträge für die Titel I’m Outta Love und Cowboys & Kisses zu ändern (Update-Anomalie).

CD_Lied (inkonsistent)
CD_ID	Albumtitel	Interpret	Gründungsjahr	Erscheinungsjahr	Track	Titel
4711	I Don't Mind	Anastacia	1999	2000	1	Not That Kind
4711	Not That Kind	Anastacia	1999	2000	2	I’m Outta Love
4711	Not That Kind	Anastacia	1999	2000	3	Cowboys & Kisses
4712	Wish You Were Here	Pink Floyd	1965	1975	1	Shine On You Crazy Diamond
4713	Freak of Nature	Anastacia	1999	2001	1	Paid my Dues

In diesem Fall wäre ein Zustand erreicht, den man als Dateninkonsistenz bezeichnet. Über die komplette Tabelle betrachtet, „passen“ die Daten nicht mehr zusammen.

Lösung

Die Daten in der Tabelle werden in zwei Tabellen aufgeteilt: CD und Lied. Die Tabelle CD enthält nur noch Felder, die voll funktional von CD_ID abhängen, hat also CD_ID als Primärschlüssel. Auch der Albumtitel allein sei eindeutig, also ein Schlüsselkandidat. Da keine weiteren (zusammengesetzten) Schlüsselkandidaten existieren, liegt die Tabelle damit automatisch in der 2. Normalform vor. Die Tabelle "Lied" enthält schließlich nur noch Felder, die voll funktional von CD_ID und Track abhängen, liegt also auch in der 2. Normalform vor. Mit Hilfe dieser verlustfreien Zerlegung sind auch die genannten Redundanzen der Daten beseitigt.

CD
CD_ID	Albumtitel	Interpret	Gründungsjahr	Erscheinungsjahr
4711	Not That Kind	Anastacia	1999	2000
4712	Wish You Were Here	Pink Floyd	1965	1975
4713	Freak of Nature	Anastacia	1999	2001

Lied
CD_ID	Track	Titel
4711	1	Not That Kind
4711	2	I’m Outta Love
4711	3	Cowboys & Kisses
4712	1	Shine On You Crazy Diamond
4713	1	Paid my Dues

Das Attribut CD_ID aus der Tabelle Lied bezeichnet man als Fremdschlüssel, der auf den Primärschlüssel der Tabelle CD verweist. Zugleich stellen die Attribute CD_ID und Track den zusammengesetzten Primärschlüssel der Tabelle Lied dar.

Dritte Normalform (3NF)

Erläuterung

Die dritte Normalform ist genau dann erreicht, wenn sich das Relationenschema in der 2NF befindet, und kein Nichtschlüsselattribut (hellgraue Zellen in der Tabelle) von einem Schlüsselkandidaten transitiv abhängt.

Ein Attribut $A_{2}$ ist vom Schlüsselkandidaten $P_{1}$ transitiv abhängig, wenn es eine Attributmenge $A_{1}$ gibt, sodass $(P_{1}\rightarrow A_{1})$ und $(A_{1}\rightarrow A_{2})$ .

Hierbei handelt es sich um eine Abhängigkeit, bei der ein Attribut $A_{2}$ über eine Attributmenge $A_{1}$ von einem Schlüsselkandidaten $P_{1}$ der Relation abhängig ist (ohne dass zugleich auch $P_{1}$ direkt von $A_{1}$ abhängig, also $A_{1}$ ein Schlüsselkandidat ist). Das heißt: Wenn die Attributmenge $A_{1}$ von der Attributmenge $P_{1}$ abhängt und Attribut $A_{2}$ von $A_{1}$ , dann ist $A_{2}$ transitiv abhängig von $P_{1}$ . Formal ausgedrückt: $(P_{1}\rightarrow A_{1})\wedge (A_{1}\rightarrow A_{2})\Rightarrow P_{1}\rightarrow A_{2}$ .

Einfach gesagt: Ein Nichtschlüsselattribut darf nicht von einer Menge aus Nichtschlüsselattributen abhängig sein. Ein Nichtschlüsselattribut darf also nur direkt von einem Primärschlüssel (bzw. einem Schlüsselkandidaten) abhängig sein.

Siehe auch: Transitive Relation, Synthesealgorithmus

Praktischer Nutzen

Transitive Abhängigkeiten sind sofort ersichtlich, ohne dass man die Zusammenhänge der Daten kennen muss. Sie sind durch die Struktur der Relationen wiedergegeben.

Außerdem werden verbliebene thematische Durchmischungen in der Relation behoben: nach der 3NF sind die Relationen des Schemas zuverlässig monothematisch.

Alternative Formulierung

Die dritte Normalform ist erreicht, wenn sich das Relationenschema in 2NF befindet, und kein Nichtschlüsselattribut (hellgraue Zellen in der Tabelle) Determinante ist.

Oder: Die dritte Normalform ist erreicht, wenn sich das Relationenschema in 2NF befindet, und kein Nichtschlüsselattribut (hellgraue Zellen in der Tabelle) von einem anderen Nichtschlüsselattribut funktional abhängig ist.

Negativbeispiel: 3NF verletzt

CD
CD_ID	Albumtitel	Interpret	Gründungsjahr	Erscheinungsjahr
4711	Not That Kind	Anastacia	1999	2000
4712	Wish You Were Here	Pink Floyd	1965	1975
4713	Freak of Nature	Anastacia	1999	2001

Lied
CD_ID	Track	Titel
4711	1	Not That Kind
4711	2	I’m Outta Love
4711	3	Cowboys & Kisses
4712	1	Shine On You Crazy Diamond
4713	1	Paid my Dues

Offensichtlich lässt sich der Albumtitel einer CD aus der CD_ID bestimmen, das Gründungsjahr der Band/Interpreten hängt wiederum vom Interpreten und damit transitiv von der CD_ID ab.

Das Problem ist hierbei wieder Datenredundanz. Wird zum Beispiel eine neue CD mit einem existierenden Interpreten eingeführt, so wird das Gründungsjahr redundant gespeichert.

Lösung

CD
CD_ID	Albumtitel	Interpret_ID	Erscheinungsjahr
4711	Not That Kind	311	2000
4712	Wish You Were Here	312	1975
4713	Freak of Nature	311	2001

Künstler
Interpret_ID	Interpret	Gründungsjahr
311	Anastacia	1999
312	Pink Floyd	1965

Lied
CD_ID	Track	Titel
4711	1	Not That Kind
4711	2	I’m Outta Love
4711	3	Cowboys & Kisses
4712	1	Shine On You Crazy Diamond
4713	1	Paid my Dues

Die Relation wird aufgeteilt, wobei die beiden voneinander abhängigen Daten in eine eigene Tabelle ausgelagert werden. Der Schlüssel der neuen Tabelle muss als Fremdschlüssel in der alten Tabelle erhalten bleiben.

An der Tabelle "Lied" wurden keine Änderungen bei der Übertragung in die 3. Normalform vorgenommen. Sie ist hier nur der Vollständigkeit halber gelistet.

Boyce-Codd-Normalform (BCNF)

Erläuterung

Ein Relationenschema ist in der Boyce-Codd-Normalform, wenn es in der 3NF ist und jede Determinante (Attributmenge, von der andere Attribute funktional abhängen) ein Schlüsselkandidat ist (oder die Abhängigkeit ist trivial).

Die BCNF (nach Raymond F. Boyce und Edgar F. Codd) verhindert, dass Teile zweier aus mehreren Feldern zusammengesetzten Schlüsselkandidaten voneinander abhängig sind.

Die Überführung in die BCNF ist zwar immer verlustfrei möglich, aber nicht immer abhängigkeitserhaltend. Die Boyce-Codd-Normalform war ursprünglich als Vereinfachung der 3NF gedacht, führte aber zu einer neuen Normalform, die diese verschärft: Eine Relation ist automatisch frei von transitiven Abhängigkeiten, wenn alle Determinanten Schlüsselkandidaten sind.

Negativbeispiel: BCNF verletzt

In diesem Beispiel gibt es eine einfache Datenbank, in der die Vereinszugehörigkeit von Sportlern gespeichert wird. Es sollen die folgenden Bedingungen gelten:

jeder Verein bietet nur eine Sportart an.
ein Sportler kann in verschiedenen Vereinen spielen, aber nur, wenn diese Vereine unterschiedliche Sportarten anbieten. Damit wird sichergestellt, dass der Sportler nie gegen einen Verein spielt, in dem er selbst Mitglied ist.

Sportler
Name	Sportart	Verein
Schuster	Fußball	FC Musterhausen
Leitner	Fußball	FC Musterhausen
Leitner	Eishockey	EC Beispielstadt

Aus den oben genannten Bedingungen folgt, dass das Attribut Sportart funktional abhängig vom Attribut Verein ist, d.h. Verein ist eine Determinante. Jedoch ist Verein kein Schlüsselkandidat. Mögliche Schlüsselkandidaten sind {Name,Verein} und {Name,Sportart}. Eine Konvertierung in BCNF ist möglich, indem (Name, Verein) als Primärschlüssel verwendet und die Relation aufgeteilt wird:

Lösung

Sportler
Name	Verein
Schuster	FC Musterhausen
Leitner	FC Musterhausen
Leitner	EC Beispielstadt

Verein
Verein	Sportart
FC Musterhausen	Fußball
EC Beispielstadt	Eishockey

Zerlegungsalgorithmus

Es existiert ein Algorithmus, der relationale Schemata durch Zerlegung (engl. decomposition) in die Boyce-Codd-Normalform überführt. Alle Schemata werden dabei solange aufgespalten, bis keines mehr die BCNF bricht. Jede Aufspaltung erfolgt anhand einer, die BCNF verletzenden, funktionalen Abhängigkeit. Die Attribute der verletzenden Abhängigkeit bilden das erste neue Schema, und die restlichen Attribute plus die Determinante ein weiteres Schema. Die beiden neuen Schemata enthalten von den ursprünglichen funktionalen Abhängigkeiten lediglich solche, welche nur Attribute des jeweiligen Schemas nutzen, der Rest geht verloren.

Folgender Pseudocode beschreibt den Zerlegungsalgorithmus:

1:	Gegeben ist ein relationales Schema $R=({\overline {R}},{\mathcal {F}})$ , mit der Menge aller Attribute ${\overline {R}}$ und der Menge der funktionalen Abhängigkeiten ${\mathcal {F}}$ über diesen Attributen.
2:	Die Ergebnismenge Dekomposition, bestehend aus den zerlegten Schemata, wird mit initialisiert.
3:	Solange es ein Schema in der Menge Dekomposition gibt, das nicht in der BCNF ist, führe folgende Zerlegung aus:
4:	Sei ${\overline {X}}{\overline {Y}}\subseteq {\overline {S}}$ eine Attributmenge für die eine funktionale Abhängigkeit ${\overline {X}}\rightarrow {\overline {Y}}$ definiert ist, welche der BCNF widerspricht.
5:	Ersetze in der Ergebnismenge Dekomposition durch zwei neue Schemata $S_{1}=({\overline {X}}{\overline {Y}},{\mathcal {F}}_{1})$ , ein Schema bestehend nur aus den Attributen der Abhängigkeit, welche die BCNF ursprünglich verletzt hat; und $S_{2}=(({\overline {S}}-{\overline {Y}})\cup {\overline {X}},{\mathcal {F}}_{2})$ , ein Schema mit allen Attributen, außer denen die nur in der abhängigen Menge ${\overline {Y}}$ und nicht in der Determinante ${\overline {X}}$ enthalten sind. Die Menge der funktionalen Abhängigkeiten ${\mathcal {F}}_{1}$ enthält nur noch die Abhängigkeiten, welche lediglich Attribute aus ${\overline {X}}{\overline {Y}}$ enthalten, entsprechendes gilt für ${\mathcal {F}}_{2}$ . Damit fallen alle Abhängigkeiten weg, welche Attribute aus beiden Schemata benötigen.
6:	Ergebnis: Dekomposition – eine Menge von relationalen Schemata, welche in der BCNF sind.

Durchlauf des Algorithmus am obigen Beispiel (ohne Darstellung aller trivialen Abhängigkeiten):

1: R = ( { Name, Sportart, Verein }, { ( { Name, Sportart } → { Verein } ), ( { Verein } → { Sportart } ), ( { Name, Verein } → { Name, Verein } ) } )
2: Dekomposition = { R }
3: da R aus Dekomposition nicht die BCNF erfüllt mache folgendes:
- 4,5: { Verein } → { Sportart } ist die Abhängigkeit, die die Verletzung der BCNF bedingt, damit ist $S_{1}$ = ( { Verein, Sportart }, { ( { Verein } → { Sportart }) } ) und $S_{2}$ = ( { Name, Verein }, { ( { Name, Verein } → { Name, Verein } ) } )
6: Ergebnis: ${\text{Dekomposition}}:=\{S_{1},S_{2}\}$

Unterschied zur 3NF

Die BCNF-Normalform ist strenger hinsichtlich der erlaubten funktionalen Abhängigkeiten: in Relationsschemata in 3NF können einige Informationen doppelt vorkommen, in der BCNF jedoch nicht.

Vierte Normalform (4NF)

Erläuterung

Ein Relationenschema ist dann in der 4. Normalform, wenn es in der BCNF ist und nur noch triviale mehrwertige Abhängigkeiten (MWA) enthält.

Einfach ausgedrückt: Es darf innerhalb einer Relation nicht mehrere 1:n- oder m:n-Beziehungen zu einem Schlüsselwert geben, die thematisch/inhaltlich nichts miteinander zu tun haben. Gehört etwa zu einem Schlüsselwert i-mal Attribut a, aber davon unabhängig auch j-mal Attribut b, ist die 4NF verletzt.

Anschaulich ausgedrückt: Die 4NF untersucht n-äre Beziehungen (mehr als zwei Tabellen stehen gleichzeitig in Beziehung) und ob diese korrekt modelliert wurden.

Negativbeispiel: 4NF verletzt

Besitz
Personnummer	Haustier	Fahrzeug
1	Katze	Volkswagen
1	Katze	Ferrari
1	Hamster	Volkswagen
1	Hamster	Ferrari
2	Hund	Porsche

Zu einer Personennummer gibt es mehrere Haustiere und Fahrzeuge. Haustiere und Fahrzeuge einer Person haben aber prinzipiell nichts miteinander zu tun; man sagt, sie sind »voneinander unabhängig«. Als Primärschlüssel kommt nur eine Kombination aus allen drei Attributen in Frage, somit ist die Tabelle in 3NF. Personnummer → Haustier ist dabei eine mehrwertige Abhängigkeit, Personnummer → Fahrzeug auch. Da diese beiden MWAs unabhängig voneinander sind, ist die 4NF verletzt.

Beispiel 4NF

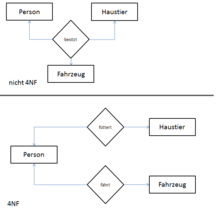
Die Beispielgrafik zeigt die fehlerhafte Modellierung der mehrwertigen Abhängigkeiten und die korrekte Lösung. Zwischen Haustier und Fahrzeug besteht keine Beziehung, somit war die Beziehung „besitzt“ falsch modelliert.

Lösung

Füttert
Personnummer	Haustier
1	Katze
1	Hamster
2	Hund

Fährt
Personnummer	Fahrzeug
1	Volkswagen
1	Ferrari
2	Porsche

Hinweis

Folgendes Relationsschema erfüllt die 4NF, obwohl auch hier mehrere MWAs vorliegen:

Elternschaft
Person	Partner	Kind
1	2	Gabi
1	88	Peter
1	99	Hilbert
2	1	Gabi
2	77	Hans

Person → Partner und Person → Kind sind zwar zwei MWAs, aber diese beiden sind auch untereinander abhängig: Partner → Kind. Solche untereinander abhängigen MWAs werden erst in 5NF gelöst.

Fünfte Normalform (5NF)

Erläuterung

Eine Relation ist in 5NF, wenn sie in der 4NF ist und keine mehrwertigen Abhängigkeiten enthält, die voneinander abhängig sind.

Einfach ausgedrückt: Es darf innerhalb einer Relation nicht mehrere 1:n- oder m:n-Beziehungen zu einem Schlüsselwert geben, die thematisch/inhaltlich miteinander verknüpft sind. Gehört etwa zu einem Schlüsselwert i-mal Attribut a, aber davon abhängig auch j-mal Attribut b, ist die 5NF verletzt.

Die 5NF verlangt also vereinfachte Relationen, aus denen aber durch Projektions- und Verbundoperationen alle Informationen der ursprünglichen Relation wiederherstellbar sein müssen. Sie ist somit sehr generell gehalten und dadurch (vorerst) die letzte Normalform. So können Relationen in einzelne Abfragen aufgeteilt werden und durch spätere Verbundsoperationen wieder zusammengefügt werden, wobei eine Teilmenge des so genannten kartesischen Produkts entsteht.

Die 5NF unterstützt in soweit die Konsistenz, als dass sich durch das Aufteilen auch neue Kombinationen ergeben können, falls beim Hinzufügen einer Information sich theoretisch auch andere Kombinationen ergeben würden, die aber nicht berücksichtigt werden, wenn alle Attribute in einer einzigen Tabelle der Relation stehen.

Negativbeispiel: 5NF verletzt

Die folgende Relation zeigt, welche Lieferanten welche Bauteile an welches Projekt liefern können:

Lieferant	Teil	Projekt
Müller	Schraube	Projekt 1
Müller	Nagel	Projekt 2
Maier	Nagel	Projekt 1

Die Relation muss weiter zerteilt werden, denn es ist auch vom Projekt abhängig, welche Teile bei diesem benötigt werden. Wichtig ist auch, dass sich die Relation aufteilen lässt, ohne dass Informationen verloren gehen.

Lösung

Um diese Relation in die 5. Normalform umzuwandeln, müssen drei Relationen erstellt werden (Lieferant–Teil, Teil–Projekt und Lieferant–Projekt).

Welche Teile kann welcher Lieferant liefern?

Lieferant-Teil
Lieferant	Teil
Müller	Schraube
Müller	Nagel
Maier	Nagel

Welche Teile werden von welchem Projekt benötigt?

Teil-Projekt
Teil	Projekt
Schraube	Projekt 1
Nagel	Projekt 2
Nagel	Projekt 1

Welche Projekte können von welchem Lieferanten beliefert werden?

Lieferant-Projekt
Lieferant	Projekt
Müller	Projekt 1
Müller	Projekt 2
Maier	Projekt 1

Hinweis

Anders als bei der Umformung zwischen den bisherigen Normalformen wird durch diese Umwandlung etwas anderes durch die neuen Relationen ausgedrückt als zuvor in der 4. Normalform.

Das merkt man leicht, wenn man die drei Relationen aus dem Beispiel oberhalb wieder vereinigt:

Lieferant	Teil	Projekt
Müller	Schraube	Projekt 1
Müller	Nagel	Projekt 2
Müller	Nagel	Projekt 1
Maier	Nagel	Projekt 1

Neu ist das Tupel: Müller – Nagel – Projekt 1.

Denn Müller könnte theoretisch das Projekt 1 mit Nägeln beliefern, da

er auch Projekt 2 mit Nägeln beliefert und
Projekt 1 auch Nägel benötigt (die jedoch bisher von Maier geliefert wurden).

Die Überführung in 5NF ist also nur dann möglich, wenn man die Möglichkeiten der Verbindungen aus drei Beziehungen ausdrücken möchte und nicht eine konkrete Verbindung zwischen den dreien haben möchte. Diese Aufteilung ergibt bei der richtigen Anwendung neue Informationen, wie hier, dass Müller Projekt 1 auch mit Nägeln beliefern könnte.

Bemerkungen

Schwächen im Datenmodell aufgrund fehlender Normalisierung können – neben den typischen Anomalien – einen höheren Aufwand bei einer späteren Weiterentwicklung bedeuten. Andererseits kann beim Datenbankentwurf aus Überlegungen zur Performance bewusst auf Normalisierungsschritte verzichtet werden (Denormalisierung). Typisches Beispiel dafür ist das Sternschema im Data-Warehouse.

Die Erstellung eines normalisierten Schemas wird durch automatische Ableitung aus einem konzeptuellen Datenmodell gestützt; hierzu dient in der Praxis ein erweitertes Entity-Relationship-Modell (ERM) oder ein Klassendiagramm der Unified Modeling Language (UML) als Ausgangspunkt. Das aus dem konzeptionellen Entwurf abgeleitete Relationenschema kann dann mit Hilfe der Normalisierungen überprüft werden; es existieren jedoch Formalismen und Algorithmen, die diese Eigenschaft bereits sicherstellen können.

Statt des ursprünglichen von Peter Chen 1976 entwickelten ER-Modells werden heute erweiterte ER-Modelle verwendet: Das Structured-ERM (SERM), das E3R-Modell, das EER-Modell sowie das von der SAP AG verwendete SAP-SERM.

Befindet sich ein Relationenschema nicht in der 1NF, so nennt man diese Form auch Non-First-Normal-Form (NF²) oder Unnormalisierte Form (UNF).

Der Prozess der Normalisierung und Zerlegung einer Relation in die 1NF, 2NF und 3NF muss die Wiederherstellbarkeit der ursprünglichen Relation erhalten, das heißt die Zerlegung muss verbundtreu und abhängigkeitstreu sein.

Merkregeln

Ist die Relation in 1. Normalform und besteht der Primärschlüssel aus nur einem Attribut und gibt es keinen anderen Schlüssel, der aus mehreren Attributen besteht, so liegt automatisch die 2. Normalform vor.
Ist eine Relation in 2. Normalform und besitzt sie außer dem Primärschlüssel höchstens ein weiteres Attribut, das nicht Teil eines Schlüssels ist, so liegt die Tabelle in 3. Normalform vor.

Literatur

Ramez Elmasri, Shamkant B. Navathe: Grundlagen von Datenbanksystemen. Pearson Studium, 2002, ISBN 3-8273-7021-3
Stefan M. Lang, Peter C. Lockemann: Datenbankeneinsatz. Springer, Berlin u.a. 1995, ISBN 3-540-58558-3.

Basierend auf einem Artikel in:

Wikipedia.de