B-Baum
Ein B-Baum (englisch B-tree) ist in der Informatik eine Daten- oder Indexstruktur, die häufig in Datenbanken und Dateisystemen eingesetzt wird. Ein B-Baum ist ein immer vollständig balancierter Baum, der Daten nach Schlüsseln sortiert speichert. Er kann binär sein, ist aber im Allgemeinen kein Binärbaum. Das Einfügen, Suchen und Löschen von Daten in B-Bäumen ist in amortisiert logarithmischer Zeit möglich. B-Bäume wachsen und schrumpfen, anders als viele Suchbäume, von den Blättern hin zur Wurzel.
Geschichte und Namensgebung
Der B-Baum wurde 1972 von Rudolf Bayer und Edward M. McCreight entwickelt. Er erwies sich als ideale Datenstruktur zur Verwaltung von Indizes für das relationale Datenbankmodell, das 1970 von Edgar F. Codd entwickelt worden war. Diese Kombination führte zur Entwicklung des ersten SQL-Datenbanksystems System R bei IBM.
Die Erfinder lieferten keine Erklärung über die Herkunft des Namens B-Baum. Die häufigste Interpretation ist, dass B für balanciert steht. Weitere Interpretationen sind B für Bayer, Barbara (nach seiner Frau), Broad, Busch, Bushy, Boeing (da Rudolf Bayer für Boeing Scientific Research Labs gearbeitet hat), Banyanbaum (ein Baum, bei dem Äste und Wurzeln ein Netz erstellen) oder binär aufgrund der ausgeführten binären Suche innerhalb eines Knotens.
Idee und Übersicht
In einem B-Baum kann ein Knoten – im Unterschied zu Binärbäumen – mehr als 2
Kind-Knoten haben. Dies ermöglicht es, mit einer variablen Anzahl Schlüssel
(oder Datenwerte) pro Knoten die Anzahl der bei einer Datensuche zu lesenden
Knoten zu reduzieren. Die maximale erlaubte Anzahl der Schlüssel ist von einem
Parameter
(in der Literatur manchmal auch als
,
oder
definiert), dem Verzweigungsgrad (oder Ordnung) des B-Baumes, abhängig. Die
Bedeutung von
ist je nach Definition unterschiedlich: Entweder bezeichnet
die maximale Anzahl von Kindknoten – in diesem Fall ist die maximal erlaubte
Anzahl von Schlüsseln
,
oder die minimal erlaubte Anzahl von Kindknoten – in dem
Fall wäre die maximal erlaubte Anzahl an Schlüsseln
.
Anwendung finden B-Bäume unter anderem bei Datenbanksystemen, die mit sehr großen Datenmengen umgehen müssen, von denen nur ein Bruchteil gleichzeitig in den Hauptspeicher eines Rechners passt. Die Daten sind daher persistent auf Hintergrundspeicher (z.B. Festplatten) abgelegt und können blockweise gelesen werden. Ein Knoten des B-Baumes kann dann als ein Block gelesen bzw. gespeichert werden. Durch den großen Verzweigungsgrad bei B-Bäumen wird die Baumhöhe und damit die Anzahl der (langsamen) Schreib-/Lesezugriffe reduziert. Die variable Schlüsselmenge pro Knoten vermeidet zusätzlich häufiges Balancieren des Baumes.
Ein vollständig besetzter B-Baum, in dem
als die maximal erlaubte Anzahl von Kindknoten und h als die Höhe des Baums
definiert ist, speichert gerade
Schlüssel. So können etwa bei einem entsprechend groß gewählten
(z.B.
)
bei einer Höhe von
bereits
Schlüssel gespeichert werden. Da eine Suchoperation höchstens
Knotenzugriffe benötigt, müssen für jede Suchanfrage in einem solchen Baum
höchstens fünf Baumknoten inspiziert werden.
Definitionen
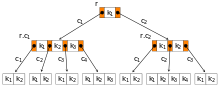
- Ein Knoten eines B-Baumes speichert
- eine variable Anzahl
von Schlüsseln
(und optional ein pro Schlüssel zugeordnetes Datenelement),
- eine Markierung isLeaf, die angibt, ob es sich bei dem Knoten um ein Blatt oder einen inneren Knoten handelt.
- Falls es sich um einen inneren Knoten handelt, zusätzlich
Verweise auf Kindknoten.
- eine variable Anzahl
- Für die Schlüssel in einem B-Baum gilt eine gegenüber binären Suchbäumen
verallgemeinerte Sortierungsbedingung:
- Alle Schlüssel eines Knotens sind aufsteigend sortiert.
- Bei einem inneren Knoten
teilen seine Schlüssel
die Schlüsselbereiche seiner Unterbäume
in
Teilbereiche ein. Jeder Schlüssel
stellt demnach eine Grenze dar, dessen linksseitiger Verweis auf kleinere Werte und dessen rechtsseitig angeordneter Verweis auf größere Werte verweist. In einem Unterbaum
kommen folglich nur Schlüssel
vor, für die gilt:
, falls
, falls
, falls
- Alle Blattknoten des B-Baumes befinden sich in gleicher Tiefe. Die Tiefe
der Blattknoten ist gleich der Höhe
des Baumes.
- Es gilt folgende Beschränkung für die erlaubte Anzahl von Kindverweisen
bzw. Schlüsseln pro Knoten. Dazu wird eine Konstante
festgelegt, die den minimalen Verzweigungsgrad von Baumknoten angibt.
- Alle Knoten außer der Wurzel haben
- mindestens
und höchstens
Schlüssel und
- mindestens
und höchstens
Kindverweise, wenn es sich um innere Knoten handelt.
- mindestens
- Die Wurzel hat
- mindestens
und höchstens
Schlüssel, wenn der B-Baum nicht leer ist, und
- mindestens
und höchstens
Kindverweise, wenn die Höhe des Baumes größer 0 ist.
- mindestens
- Alle Knoten außer der Wurzel haben
Eigenschaften
Für die Höhe
eines B-Baumes mit
gespeicherten Datenelementen gilt:
Damit sind im schlimmsten Fall immer noch Zugriffe auf
Baumknoten zum Auffinden eines Datenelements notwendig. Die Konstante dieser
Abschätzung ist aber deutlich geringer als bei (balancierten) binären
Suchbäumen mit Höhe
:
Bei einem minimalen Verzweigungsgrad von
benötigt ein B-Baum damit Zugriffe auf zehnmal weniger Knoten zum Auffinden
eines Datenelements. Wenn der Zugriff auf einen Knoten die Dauer der gesamten
Operation dominiert (wie das beim Zugriff auf Hintergrundspeicher der Fall ist),
ergibt sich dadurch eine zehnfach erhöhte Ausführungsgeschwindigkeit.
Spezialfälle und Varianten
Für den Spezialfall
spricht man von 2-3-4-Bäumen,
da Knoten in einem solchen Baum 2, 3 oder 4 Kinder haben können. Verbreitete
Varianten des B-Baumes sind B+-Bäume,
in denen die Daten nur in den Blättern gespeichert werden, und B*-Bäume, die durch eine
modifizierte Überlaufbehandlung immer zu
gefüllt sind. Alle diese Varianten werden wie auch der reguläre B-Baum in der
Praxis oft eingesetzt.
Auch ein R-Baum kann als balancierter Baum als Erweiterung des B-Baumes bezeichnet werden.
Operationen
Suchen
Die Suche nach einem Schlüssel
liefert denjenigen Knoten
,
der diesen Schlüssel speichert, und die Position
innerhalb dieses Knotens, für die gilt, dass
.
Enthält der Baum den Schlüssel
nicht, liefert die Suche das Ergebnis nicht enthalten.
Die Suche läuft in folgenden Schritten ab:
- Die Suche beginnt mit dem Wurzelknoten
als aktuellem Knoten
.
- Ist
ein innerer Knoten,
- wird die Position
des kleinsten Schlüssels bestimmt, der größer oder gleich
ist.
- Existiert eine solche Position
,
- aber ist
, kann der gesuchte Schlüssel nur in dem Unterbaum mit Wurzel
enthalten sein. Die Suche wird daher mit Schritt 2 und dem Knoten
als aktuellem Knoten fortgesetzt.
- ansonsten wurde der Schlüssel gefunden und
wird als Ergebnis zurückgeliefert.
- aber ist
- Existiert keine solche Position, ist der Schlüssel größer als alle im
aktuellen Knoten gespeicherten Schlüssel. In diesem Fall kann der gesuchte
Schlüssel nur noch in dem Unterbaum enthalten sein, auf den der letzte
Kindverweis
zeigt. In diesem Fall wird die Suche mit Schritt 2 und dem Knoten
als aktuellem Knoten fortgesetzt.
- wird die Position
- Ist
ein Blattknoten,
- Wird
in den Schlüsseln von
gesucht.
- Wenn der Schlüssel an Position
gefunden wird, ist das Ergebnis
, ansonsten nicht enthalten.
- Wird
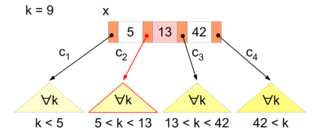
In Abbildung 2 ist die Situation während der Suche nach dem Schlüssel
dargestellt. Im Schritt 2 aus obigem Algorithmus wird im aktuellen Knoten
die kleinste Position
gesucht, für die
gilt. Im konkreten Beispiel wird die Position
gefunden, da
gilt. Die Suche wird daher im rot markierten Unterbaum
fortgesetzt, weil sich aufgrund der B-Baum-Eigenschaft (2) der gesuchte
Schlüssel
nur in diesem Unterbaum befinden kann.
Einfügen
Das Einfügen eines Schlüssels
in einen B-Baum geschieht immer in einem Blattknoten.
- In einem vorbereitenden Schritt wird der Blattknoten
gesucht, in den eingefügt werden muss. Dabei werden Vorkehrungen getroffen, damit die Einfügeoperation nicht die B-Baum-Bedingungen verletzt und einen Knoten erzeugt, der mehr als
Schlüssel enthält.
- In einem abschließenden Schritt wird
unter Berücksichtigung der Sortierreihenfolge lokal in
eingefügt.
Die Suche von
läuft mit zwei Unterschieden so ab, wie unter Suchen
beschrieben. Diese Unterschiede sind:
- Das Einfügen eines neuen Schlüssels
geschieht immer in einem Blattknoten. Dem Einfügen muss daher immer ein vollständiger Suchlauf vorhergehen, der ergibt, dass der Schlüssel
noch nicht existiert, und der ermittelt, in welchen Knoten er einzutragen ist. Dies kann nur ein Blattknoten sein, denn diese Aussage ist erst nach dem Durchsuchen über die gesamte Höhe des Baumes zulässig. Die Suche bricht jedoch in einem inneren Knoten ab, wenn dort der Schlüssel
bereits gefunden wird und ein Einfügen deshalb nicht notwendig ist.
- Bevor die Suche zu einem Kindknoten
absteigt, wird überprüft, ob
voll ist, d.h. bereits
Schlüssel enthält. In diesem Fall wird
vorsorglich geteilt. Dies garantiert, dass die Einfügeoperation mit einem einzigen Baumabstieg durchgeführt werden kann und keine anschließenden Reparaturmaßnahmen zur Wiederherstellung der B-Baum-Bedingungen durchgeführt werden müssen.
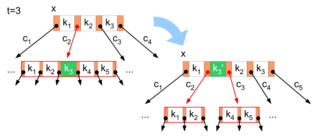
Das Teilen eines vollen Baumknotens geschieht, wie in Abbildung 3 gezeigt.
Die Suche ist an Knoten
angekommen und würde zum Kindknoten
absteigen (roter Pfeil). Das heißt, die Suchposition ist
.
Da dieser Kindknoten voll ist, muss er vor dem Abstieg geteilt werden, um zu
garantieren, dass ein Einfügen möglich ist. Ein voller Knoten hat mit
immer eine ungerade Anzahl von Schlüsseln. Der mittlere davon (in der Abbildung
ist das Schlüssel
)
wird im aktuellen Knoten an der Suchposition
eingefügt. Der Knoten
wird in zwei gleich große Knoten mit jeweils
Schlüsseln geteilt und diese über die beiden neuen Zeigerpositionen verlinkt
(zwei rote Pfeile im Ergebnis). Die Suche steigt anschließend entweder in den
Unterbaum
oder
ab, je nachdem, ob der einzufügende Schlüssel kleiner oder gleich dem mittleren
Schlüssel des geteilten Knotens ist oder nicht.
Löschen
Das Löschen eines Schlüssels
ist eine komplexere Operation als das Einfügen, da hier auch der Fall betrachtet
werden muss, dass ein Schlüssel aus einem inneren Knoten gelöscht wird. Der
Ablauf ist dabei wie die Suche nach einem geeigneten Platz zum Einfügen eines
Schlüssels, allerdings mit dem Unterschied, dass vor dem Abstieg in einen
Unterbaum überprüft wird, ob dieser genügend Schlüssel (
)
enthält, um eine eventuelle Löschoperation ohne Verletzung der
B-Baum-Bedingungen durchführen zu können. Dieses Vorgehen ist analog zum
Einfügen und vermeidet anschließende Reparaturmaßnahmen.
Enthält der Unterbaum, den die Suche für den Abstieg ausgewählt hat, die
minimale Anzahl von Schlüsseln (),
wird entweder eine Verschiebung oder
eine Verschmelzung
durchgeführt. Wird der gesuchte Schlüssel in einem Blattknoten gefunden, kann er
dort direkt gelöscht werden. Wird er dagegen in einem inneren Knoten gefunden,
passiert die Löschung wie in Löschen
aus inneren Knoten beschrieben.
Verschiebung
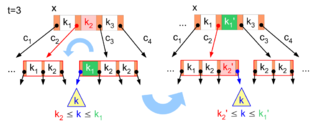
Enthält der für den Abstieg ausgewählte Unterbaum nur die minimale
Schlüsselanzahl ,
aber ein vorausgehender oder nachfolgender Geschwisterknoten hat mindestens
Schlüssel, wird ein Schlüssel in den ausgewählten Knoten verschoben, wie in
Abbildung 4 gezeigt. Die Suche hat hier
für den Abstieg ausgewählt (da
),
dieser Knoten enthält aber nur
Schlüssel (roter Pfeil). Da der nachfolgende Geschwisterknoten
ausreichend viele Schlüssel enthält, kann von dort der kleinste Schlüssel
in den Vaterknoten verschoben werden, um im Gegenzug den Schlüssel
als zusätzlichen Schlüssel in den für den Abstieg ausgewählten Knoten zu
verschieben. Dazu wird der linke Unterbaum von
zum neuen rechten Unterbaum des verschobenen Schlüssels
.
Man kann sich leicht davon überzeugen, dass diese Rotation die
Sortierungsbedingungen erhält, da für alle Schlüssel
im verschobenen Unterbaum vor und nach der Verschiebung die Forderung
gilt. Eine symmetrische Operation kann zur Verschiebung eines Schlüssels aus
einem vorausgehenden Geschwisterknoten durchgeführt werden.
Verschmelzung
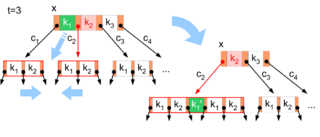
Enthalten sowohl der für den Abstieg ausgewählte Unterbaum
als auch sein unmittelbar vorausgehender und nachfolgender Geschwisterknoten
genau die minimale Schlüsselanzahl, ist eine Verschiebung
nicht möglich. In diesem Fall wird eine Verschmelzung des ausgewählten
Unterbaumes mit dem vorausgehenden oder nachfolgenden Geschwisterknoten gemäß
Abbildung 5 durchgeführt. Dazu wird der Schlüssel aus dem Vaterknoten
,
welcher die Wertebereiche der Schlüssel in den beiden zu verschmelzenden Knoten
trennt, als mittlerer Schlüssel in den verschmolzenen Knoten verschoben. Die
beiden Verweise auf die jetzt verschmolzenen Kindknoten werden durch einen
Verweis auf den neuen Knoten ersetzt.
Da der Algorithmus vor dem Abstieg in einen Knoten sicherstellt, dass dieser
mindestens
anstelle der von den B-Baum-Bedingungen geforderten
Schlüssel enthält, ist gewährleistet, dass der Vaterknoten
eine ausreichende Schlüsselanzahl enthält, um einen Schlüssel für die
Verschmelzung zur Verfügung zu stellen. Nur im Fall, dass zwei Kinder des
Wurzelknotens verschmolzen werden, kann diese Bedingung verletzt sein, da die
Suche bei diesem Knoten beginnt. Die B-Baum-Bedingungen fordern für den
Wurzelknoten mindestens einen Schlüssel, wenn der Baum nicht leer ist. Bei
Verschmelzung der letzten zwei Kinder des Wurzelknotens, wird aber sein letzter
Schlüssel in das neu entstehende einzige Kind verschoben, was zu einem leeren
Wurzelknoten in einem nicht leeren Baum führt. In diesem Fall wird der leere
Wurzelknoten gelöscht und durch sein einziges Kind ersetzt.
Löschen aus inneren Knoten
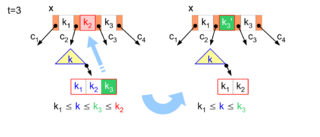
Wird der zu löschende Schlüssel
bereits in einem inneren Knoten gefunden (
in Abbildung 6), kann dieser nicht direkt gelöscht werden, weil er für die
Trennung der Wertebereiche seiner beiden Unterbäume
und
benötigt wird. In diesem Fall wird sein symmetrischer Vorgänger (oder sein
symmetrischer Nachfolger) gelöscht und an seine Stelle kopiert. Der symmetrische
Vorgänger ist der größte Blattknoten im linken Unterbaum
,
befindet sich also dort ganz rechts außen. Der symmetrische Nachfolger ist
entsprechend der kleinste Blattknoten im rechten Unterbaum
und befindet sich dort ganz links außen. Die Entscheidung, in welchen Unterbaum
der Abstieg für die Löschung stattfindet, wird davon abhängig gemacht, welcher
genügend Schlüssel enthält. Haben beide nur die minimale Schlüsselanzahl, werden
die Unterbäume verschmolzen. Damit wird keine Trennung der Wertebereiche mehr
benötigt und der Schlüssel kann direkt gelöscht werden.
Beispiel
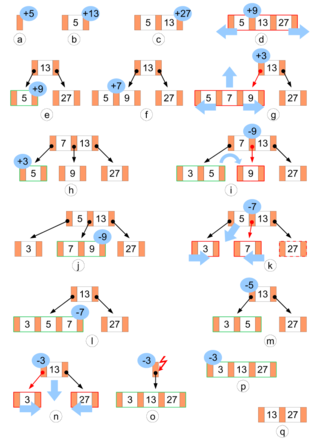
Abbildung 7 zeigt die Entwicklung eines B-Baumes mit minimalem
Verzweigungsgrad .
Knoten in einem solchen Baum können minimal einen und maximal drei Schlüssel
speichern und haben zwischen zwei und vier Verweise auf Kindknoten. Man spricht
daher auch von einem 2-3-4-Baum.
In einer praktischen Anwendung würde man dagegen einen B-Baum mit wesentlich
größerem Verzweigungsgrad verwenden.
Folgende Operationen wurden auf einem 2-4 Baum (siehe Abbildung 7) durchgeführt:
- a–c) Einfügen von 5, 13 und 27 in einen anfangs leeren Baum.
- d–e) Einfügen von 9 führt zum Teilen des Wurzelknotens.
- f) Einfügen von 7 in einen Blattknoten.
- g–h) Einfügen von 3 führt zum Teilen eines Knotens.
- i–j) Um 9 löschen zu können, wird ein Schlüssel aus einem Geschwisterknoten verschoben.
- k–l) Das Löschen von 7 führt zum Verschmelzen von zwei Knoten.
- m) Löschen von 5 aus einem Blatt.
- n–q) Löschen von 3 führt zur Verschmelzung der letzten zwei Kinder des Wurzelknotens. Der entstehende leere Wurzelknoten wird durch sein einziges Kind ersetzt.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.03. 2022