B+-Baum
Der B+-Baum ist eine in Datenbanken und Dateisystemen verwendete Daten- oder Indexstruktur. Sie ist eine Erweiterung des B-Baumes. Bei einem B+-Baum werden die eigentlichen Datenelemente nur in den Blattknoten gespeichert, während die inneren Knoten lediglich Schlüssel enthalten. Die Schlüssel in den Verzeichnisseiten bezeichnet man auch als Separatoren.
Der B+-Baum wird aus historischen Gründen manchmal auch als B*-Baum bezeichnet. B*-Baum bezeichnet jedoch auch eine B-Baum-Variante mit einem Mindestfüllgrad von 2/3 durch eine verbesserte Split-Strategie.
Ziel dieses Verfahrens ist es, die Zugriffszeiten auf die Datenelemente zu verbessern. Dazu muss man die Baumhöhe verringern, was bedeutet, dass der Verzweigungsgrad des Baumes wachsen muss. Da die maximale Speicherbelegung eines Knotens begrenzt ist, gewinnt man durch das Verlegen der Daten in die Blätter mehr Platz für Schlüssel bzw. Verzweigungen in den inneren Knoten. Dies gilt insbesondere bei der Speicherung komplexer Objekte, die deutlich mehr Speicher belegen als die Schlüssel oder auch nicht über eine feste Größe verfügen. Die reduzierte Baumhöhe impliziert auch weniger innere Knoten. Diese können so leichter im Hauptspeicher gehalten werden, was die Leistung im wahlfreien Zugriff steigert.
Ein weiteres Ziel kann sein, die Operation Bereichssuche zu verbessern, bei der alle Daten in einem gewissen Schlüsselintervall sequentiell durchlaufen werden. Werden die Daten nämlich ausschließlich in den Blättern abgelegt, muss der jeweils nächste Datensatz der Sequenz nicht wieder von der Wurzel aus gesucht werden. So muss für einen Komplettdurchlauf der Daten nur der erste Schlüssel gesucht werden, ein Großteil des Baumes wird nicht gelesen. Um Nachfolger und Vorgänger eines Blattknoten effizient (d.h. in konstanter Zeit) zu finden, müssen die Blätter in einer doppelt verketteten Liste miteinander verbunden sein. Dieses Feature wird häufig in die Definition des B+-Baumes mit aufgenommen.
Wesentlicher Vorteil eines externen Suchbaums (Daten nur in den Blättern) ist die Möglichkeit des Einsatzes von Sekundärindizes. Sie stellen einen weiteren – nach anderen Kriterien sortierbaren – Suchbaum auf denselben Daten zur Verfügung.
Struktur
Jeder Knoten besteht aus
Suchschlüsseln und
Pointern. Blattnachfolger und (optional) Blattvorgänger werden in jedem Blatt
gespeichert. Die restlichen Pointer in den Blattknoten zeigen jeweils auf die
Datenelemente, die durch die Suchschlüssel repräsentiert werden.
Es ist auch möglich, Mittelknoten und Wurzel-/Blattknoten unterschiedliche
Größen zuzuordnen. Hier spricht man von einem Baum des Typs ,
wobei
die Größe von Mittelknoten und
die Größe von Wurzel- und Blattknoten bezeichnet. Im Folgenden gilt
.
Beispiel:
- Alle Knoten haben maximal 3 Suchschlüsselwerte und maximal 4 Pointer
- Die Wurzel hat mindestens einen Wert, also 2 Pointer
- Innere Knoten haben mindestens 1 Suchschlüssel und 2 Pointer
- Blätter haben mindestens 2 Suchschlüssel und 3 Pointer
Regeln
- Wurzel: Mindestens zwei Pointer besetzt
- Mittelknoten: Mindestfüllgrad
Pointer
- Blätter: Mindestfüllgrad
Pointer (zeigen auf Datenblöcke, Pointer auf Nachbarknoten werden nicht gezählt)
Für Mittel- und Wurzelknoten gilt: Der links unter einem Suchschlüssel startende Pointer führt zu einem Knoten, dessen größter Suchschlüsselwert kleiner dem Suchschlüsselwert ist. Der rechts unter einem Suchschlüssel stehende Pointer führt zu einem Knoten, dessen kleinster Suchschlüsselwert größer gleich dem Suchschlüsselwert ist.
Operationen
Suchen
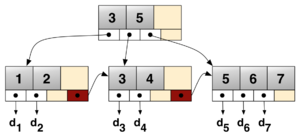
Beispiel anhand von obiger Grafik:
- Suche von Wert „9“: Start im Wurzelknoten, Wert ist größer als oder gleich 5, also gehe rechten Weg den Pointer entlang, durchsuche Blatt, nicht gefunden, Suche erfolglos.
- Suche von Wert „2“: Start im Wurzelknoten, Wert ist kleiner als 3, also gehe linken Weg dem Pointer entlang und durchsuche Blatt, gefunden, Suche erfolgreich.
Einfügen
Es gibt grundsätzlich zwei Möglichkeiten beim Einfügen von neuen Suchschlüsseln:
- Es gibt im betreffenden Blatt Platz.
- Es gibt keinen Platz.
Im ersten Fall kann der Wert einfach in das Blatt eingetragen werden (siehe Suchen).
Im zweiten Fall wird der Wert an das Blatt „virtuell“ angefügt. Jetzt ergibt sich eine Überfüllung des Blattes. Es muss also geteilt werden. Dabei ist zu beachten, dass bei ungerader Suchschlüsselanzahl in einem Blatt das linke Teilblatt einen Suchschlüsselwert mehr als das rechte bekommt (Beispiel: n=4, 1 einfügen, links 3 Werte, rechts 2 Werte). Dies kann möglicherweise eine Kettenreaktion verursachen, die nach oben im Baum durchpropagiert werden muss, da ja die Mittel- und Wurzelknoten angepasst werden müssen. Bei dieser Kettenreaktion wird bei der Überfüllung eines Eltern-Knotens das mittlere Element eine Ebene nach oben befördert. Das wiederholt sich, bis genügend Platz ist, oder der B+-Baum um eine Ebene (Tiefe) erweitert werden muss.
Löschen
Der Wert wird im Baum gesucht. Wenn er gefunden wird, dann wird der Wert entfernt. Eventuelle Änderungen müssen durch den Baum propagiert werden. Dabei gibt es zu beachten, dass unterbefüllte Knoten mit anderen verschmolzen oder Schlüssel von Geschwisterknoten umverteilt werden müssen. Beim Verschmelzen gibt es durchaus unterschiedliche Techniken. Am gebräuchlichsten sollte es sein, den Knoten mit seinem linken Nachbarn zu verschmelzen (wenn es keinen linken gibt, dann den rechten) und bei Bedarf diesen bei Überfüllung wieder nach obiger Regel zu teilen.
Vorteile
- Der B+-Baum ist immer balanciert
- höherer Verzweigungsgrad als der B-Baum, und damit eine geringere Verzeichnisgröße und Tiefe
- für Bereichsanfragen (in Datenbanksystem) optimal geeignet, da immer alle Blätter sortiert und durch Pointer untereinander verbunden, sodass leicht iterierbar
- Referenzschlüssel entsprechen nicht zwingend einem realen Schlüssel und müssen daher nur in manchen Fällen beim Löschen eines entsprechenden Knotens gelöscht werden.
Varianten
Eine wichtige Variante des B+-Baums erlaubt die Verwendung von Schlüsseln und
Daten mit variabler Länge. Hierzu muss der Begriff des Füllgrades umdefiniert
werden, da größere Schlüssel natürlich mehr Speicherplatz benötigen als kleine
Schlüssel. Ziel des Baumes bleibt weiterhin, alle Seiten mindestens zur Hälfte
gefüllt zu lassen, und es werden die entsprechenden Balancierungs-Operationen
weiterhin durchgeführt. Bei Löschvorgängen kann jedoch der Mindestfüllgrad
unterschritten werden, wenn ein zu großer Separator die entsprechende
Balancierungs-Operation verhindert. Es kann dann für Verzeichnisseiten nur noch
der Mindestfüllgrad
ohne komplizierte Restrukturierungsmaßnahmen garantiert werden.
Durch Verwendung einer Varint-Kodierung kann der Verzweigungsgrad eines B+-Baumes, wenn die Implementierung variable Längen erlaubt, meist deutlich gesteigert werden.
Mit Schlüsseln variabler Länge kann ein B+-Baum auch als Trie (Präfix-B+-Baum) eingesetzt werden.
Literatur
- Alfons Kemper, André Eickler: Datenbanksysteme. Oldenbourg Verlag, München 2015, ISBN 978-3-11-044375-2 (10. Auflage)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.03. 2022