Molekülstruktur
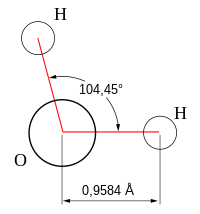
Als Molekülstruktur oder Molekülgeometrie wird die
geometrische, räumliche relative Anordnung der Atome
in einem Molekül bezeichnet. Sie
bestimmt maßgeblich wichtige Eigenschaften wie das elektrische
Dipolmoment.
Eigenschaften
Zur Beschreibung werden meist kartesische
Koordinaten (x, y, z) verwendet, um die Positionen der Atome anzugeben, oder
auch interne Koordinaten, d.h. Bindungslängen
und Bindungswinkel
und ggf. Diederwinkel.
Diese können durch das Auftreten von Symmetrien
usw. in 32 Punktgruppen
zusammengefasst werden. Die Beschreibung erfolgt typischerweise in der nach Arthur
Schoenflies benannten Schoenflies-Symbolik.
Experimentell kann die Molekülstruktur mittels
Kristallstrukturanalyse
oder Kernspinresonanzspektroskopie
(NMR) ermittelt werden. Für kleine Moleküle aus wenigen Atomen kann die Struktur
auch mit den Methoden der Theoretischen
Chemie berechnet werden. Eine ungefähre Abschätzung ist mit dem VSEPR-Modell möglich.
| Atome am Zentralatom | Freie Elektronenpaare | Sterische Zahl | Form | Idealer Bindungswinkel (Bsp.) | Beispiel | Bild |
|---|---|---|---|---|---|---|
| 2 | 0 | 2 | linear | 180° | CO2 | |
| 3 | 0 | 3 | trigonal-planar | 120° | BF3 | |
| 2 | 1 | 3 | gebogen | 120° (119°) | SO2 | |
| 4 | 0 | 4 | tetraedrisch | 109,5° | CH4 | 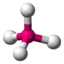 |
| 3 | 1 | 4 | trigonal-pyramidal | 109,5° (107,8°) | NH3 | |
| 2 | 2 | 4 | gebogen | 109,5° (104,48°) | H2O | |
| 5 | 0 | 5 | trigonal-bipyramidal | 90°, 120° | PCl5 | 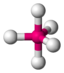 |
| 4 | 1 | 5 | wippenartig | ax–ax 180° (173,1°), eq–eq 120° (101,6°), ax-eq 90° |
SF4 | |
| 3 | 2 | 5 | T-förmig | 90° (87,5°), 180° (175°) | ClF3 | |
| 2 | 3 | 5 | linear | 180° | XeF2 | |
| 6 | 0 | 6 | octaedrisch | 90°, 180° | SF6 | 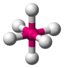 |
| 5 | 1 | 6 | quadratisch-pyramidal | 90° (84,8°) | BrF5 | |
| 4 | 2 | 6 | quadratisch-planar | 90°, 180° | XeF4 | |
| 7 | 0 | 7 | pentagonal-bipyramidal | 90°, 72°, 180° | IF7 | 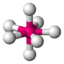 |
| 6 | 1 | 7 | pentagonal-pyramidal | 72°, 90°, 144° | XeOF5− | |
| 5 | 2 | 7 | pentagonal-planar | 72°, 144° | XeF5− | |
| 8 | 0 | 8 | quadratisch-antiprismatisch | XeF8(2−) | ||
| 9 | 0 | 9 | tricapped trigonal-prismatisch | ReH9(2−) |  |
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.06. 2024