Strahldichte
| Physikalische Größe | |||||||
|---|---|---|---|---|---|---|---|
| Name | Strahldichte | ||||||
| Formelzeichen | |||||||
| |||||||
Die Strahldichte L (auch spezifische Intensität, englisch radiance) liefert detaillierte Information über die Orts- und Richtungsabhängigkeit der von einer Sendefläche abgegebenen Strahlung.
Definition
Einführung und Grenzwertbetrachtung
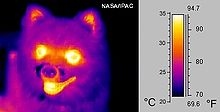
Man betrachte einen Körper (beispielsweise eine Glühlampe, eine Leuchtdiode), welcher Strahlung (gemessen beispielsweise in Watt) in seine Umgebung abgibt. In der Regel wird jeder Punkt des Körpers in verschiedene Richtungen unterschiedlich viel Strahlung aussenden. Soll diese Charakteristik detailliert beschrieben werden, so ist das Konzept der Strahldichte nötig.
Es ist nämlich nicht möglich anzugeben, wie viel Watt von einem unendlich kleinen Punkt auf der Oberfläche des Körpers ausgeht, da sich die endliche Strahlungsleistung auf eine unendliche Anzahl solcher Punkte verteilt und auf einen einzelnen Oberflächenpunkt daher Null Watt entfallen. Stattdessen betrachtet man eine kleine Umgebung des betreffenden Punktes, setzt die von dieser Umgebung ausgehende (endliche) Strahlungsleistung ins Verhältnis zu ihrer (endlichen) Fläche und lässt die Umgebung gedanklich auf Null schrumpfen. Obwohl die abgestrahlte Leistung und auch die abstrahlende Fläche dabei jeweils gegen Null gehen, strebt beider Verhältnis gegen einen endlichen Grenzwert, die Flächenleistung oder spezifische Ausstrahlung M des Punktes, gemessen in Watt pro Quadratmeter.

In gleicher Weise ist es nicht möglich anzugeben, welche Leistung in eine bestimmte Richtung abgegeben wird, da sich die endliche Strahlungsleistung auf unendlich viele mögliche Richtungen verteilt und auf jede einzelne Richtung daher Null Watt entfallen. Stattdessen betrachtet man einen kleinen, die gewünschte Richtung umgebenden Raumwinkel, setzt die in diesen Raumwinkel abgegebene (endliche) Leistung ins Verhältnis zur (endlichen) Größe des Raumwinkels und lässt den Raumwinkel gedanklich auf Null schrumpfen. Wiederum streben dabei sowohl der Raumwinkel als auch die in ihm enthaltene abgestrahlte Leistung jeweils gegen Null, ihr Verhältnis aber gegen einen endlichen Grenzwert, die in die betreffende Richtung abgegebene Strahlstärke I, gemessen in Watt pro Steradiant.
Die Strahldichte kombiniert beides und beschreibt auf diese Weise sowohl die Orts- als auch die Richtungsabhängigkeit der von einem unendlich kleinen Flächenelement abgegebenen Strahlung.
Strahldichte
Die Strahldichte
gibt an, welche Strahlungsleistung
von einem gegebenen Punkt der Strahlungsquelle in die durch den Polarwinkel
und den Azimutwinkel
gegebene Richtung pro projiziertem Flächenelement
und pro Raumwinkelelement
ausgesendet wird.
ist hierbei der Winkel zwischen Ausstrahlrichtung und Flächennormale
- Formelzeichen: L, LΩ
- SI-Einheit: Watt pro Quadratmeter pro Steradiant
- Einheitenzeichen: W·m−2·sr−1
Die Definition der Strahldichte weist die Besonderheit auf, dass die
abgegebene Strahlungsleistung nicht wie üblich auf das abstrahlende
Flächenelement ,
sondern auf das in Abstrahlrichtung projizierte Flächenelement
bezogen wird. Die in eine bestimmte Richtung abgegebene Strahlungsleistung hängt
nämlich zum einen von den (möglicherweise richtungsabhängigen) physikalischen
Strahlungseigenschaften der Oberfläche und zum anderen rein geometrisch von der
in Abstrahlrichtung wirksamen Projektion des strahlenden Flächenelements ab. Der
zweite Effekt bewirkt, dass die unter dem Polarwinkel
abgegebene Strahlungsleistung um den Faktor
geringer ist als die senkrecht abgegebene Leistung. Die Division durch den
Faktor
rechnet diesen geometrischen Effekt heraus, so dass nur noch eine eventuelle
physikalische Richtungsabhängigkeit aufgrund der Oberflächeneigenschaften übrig
bleibt.
Oberflächen, welche nach Herausrechnen des –Faktors
keine Richtungsabhängigkeit der Strahldichte mehr aufweisen, nennt man
diffuse Strahler oder lambertsche
Strahler. Ein lambertsches Flächenelement gibt in alle Richtungen
dieselbe Strahldichte ab:
Die von ihm in eine bestimmte Richtung abgegebene Strahlungsleistung variiert nur noch mit dem Kosinus des Abstrahlwinkels; solche Strahler sind daher mathematisch besonders einfach zu behandeln:
Insbesondere kann bei der Integration über den Raumwinkel die nunmehr
winkelunabhängige Strahldichte
als Konstante vor das Integral gezogen werden (siehe unten).
Für die Definition der Strahldichte ist es unerheblich, ob es sich bei der vom Flächenelement abgegebenen Strahlung um (thermische oder nichtthermische) Eigenemission, um transmittierte oder reflektierte Strahlung oder eine Kombination daraus handelt.
Die Strahldichte ist an jedem Punkt des Raumes definiert, an dem Strahlung vorhanden ist. Man denke sich anstelle eines abstrahlenden Oberflächenelements gegebenenfalls ein fiktives durchstrahltes Flächenelement im Raum.
Das photometrische Äquivalent der Strahldichte ist die Leuchtdichte, welche daher zur Veranschaulichung dienen kann: Die Leuchtdichte ist ein Maß für die Helligkeit, mit der eine Fläche wahrgenommen wird. Betrachtet man eine diffus leuchtende Fläche, z. B. ein Blatt Papier, aus verschiedenen Richtungen, so bleibt die wahrgenommene Leuchtdichte der Fläche dabei konstant, während die den Betrachter erreichende gesamte Lichtmenge von der projizierten Fläche abhängt und daher mit dem Cosinus des Betrachtungswinkels variiert. Analog ist die Strahldichte eines diffusen Strahlers in alle Richtungen dieselbe, die in eine bestimmte Richtung abgegebene Strahlungsleistung hängt aber zusätzlich von der in die betreffende Richtung projizierten Strahlfläche ab.
Spektrale Strahldichte
Die spektrale Strahldichte (engl. spectral radiance)
(Einheit: W·m−2·Hz−1·sr−1) eines Körpers gibt
an, welche Strahlungsleistung der Körper bei der Frequenz
in die durch den Polarwinkel
und den Azimutwinkel
gegebene Richtung pro projizierter Fläche, pro Raumwinkel
und pro Frequenzbreite aussendet.
Die spektrale Strahldichte wird auch angegeben als
(Einheit: W·m−3·sr−1) bezogen auf das
Einheits-Wellenlängenintervall.
Die spektrale Strahldichte liefert die detaillierteste Darstellung der Strahlungseigenschaften eines Strahlers. Sie beschreibt explizit die Richtungsabhängigkeit und die Frequenz- (oder Wellenlängen‑)abhängigkeit der abgegebenen Strahlung. Aus der spektralen Strahldichte lassen sich die anderen Strahlungsgrößen durch Integration über die Richtungen und/oder Frequenzen ableiten. Integration über das relevante Frequenz- bzw. Wellenlängenintervall liefert insbesondere wieder die Strahldichte, welche daher, wenn sie von der spektralen Strahldichte unterschieden werden muss, auch Gesamtstrahldichte genannt wird.
Schwarzer Strahler
Ein Schwarzer Strahler ist ein idealisierter Körper, welcher alle auf ihn treffende elektromagnetische Strahlung vollständig absorbiert. Aus thermodynamischen Gründen weist die von einem solchen Körper seinerseits abgegebene thermische Strahlung ein universelles Spektrum auf, und er muss zwangsläufig ein lambertscher Strahler sein. Reale Strahler erreichen diese idealen Eigenschaften niemals vollständig, können ihnen jedoch nahekommen. Die Strahlungseigenschaften eines Schwarzen Strahlers können daher oft als gute Näherung für einen realen Strahler benutzt werden.
Die Abweichung eines realen Strahlers vom schwarzen Ideal kann durch einen Emissionsgrad erfasst werden. Da ein realer Strahler auf einer gegebenen Wellenlänge nicht stärker strahlen kann als ein schwarzer Körper gleicher Temperatur, muss der Emissionsgrad immer kleiner als 1 sein. Der Emissionsgrad kann wellenlängenabhängig und, falls der reale Strahler kein lambertscher Strahler ist, auch richtungsabhängig sein. Ermittelt werden die Emissionsgrade durch Vergleich der Strahldichten oder der spektralen Strahldichten von realem und Schwarzem Strahler.
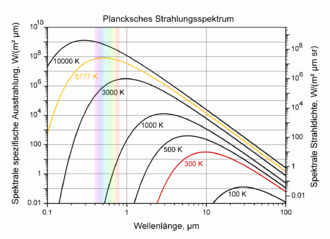
Spektrale Strahldichte eines Schwarzen Strahlers
Herleitung
Nach Planck gilt für die spektrale Energiedichte eines Schwarzen Strahlers:
Aus dieser ergibt sich die spektrale Strahldichte:
Der Faktor kann so verstanden werden, dass sich die Strahlung mit der
Geschwindigkeit
in den gesamten Raumwinkel
ausbreitet.
Folgerung
Für die spektrale Strahldichte
eines Schwarzen
Strahlers der absoluten
Temperatur T gilt nach Max Planck
in der Frequenzdarstellung:
mit
| : | spektrale Strahldichte des Schwarzen Strahlers, | W m−2 Hz−1 sr−1 | |
| : | Frequenz, | Hz |
und in der Wellenlängendarstellung:
mit
| : | spektrale Strahldichte des Schwarzen Strahlers, | W m−2 μm−1 sr−1 | |
| : | Wellenlänge, | m, µm | |
| : | absolute Temperatur, | K | |
| : | Plancksches Wirkungsquantum, | Js | |
| : | Lichtgeschwindigkeit, | m/s | |
| : | Boltzmannkonstante, | J/K |
ist die Strahlungsleistung, die vom Flächenelement dA im Frequenzbereich
zwischen ν und ν + dν in das zwischen den Azimutwinkeln
φ und φ+dφ sowie den Polarwinkeln β und
β+dβ aufgespannte Raumwinkelelement dΩ abgestrahlt wird.
Die Richtungsabhängigkeit dieser Strahlungsleistung kommt nur durch den
geometrischen
–Faktor
zustande; die spektrale Strahldichte selbst ist richtungsunabhängig.
Bei der Umrechnung zwischen Frequenz- und Wellenlängendarstellung ist zu beachten, dass wegen
gilt:
Das Verhältnis der in eine bestimmte Richtung abgegebenen und bei einer bestimmten Wellenlänge betrachteten spektralen Strahldichte eines Flächenelements eines gegebenen Strahlers zu der bei derselben Wellenlänge betrachteten spektralen Strahldichte eines Schwarzen Strahlers derselben Temperatur ist der gerichtete spektrale Emissionsgrad des Flächenelements.
Integriert man die spektrale Strahldichte des Schwarzen Strahlers über alle
Richtungen des Halbraums, in den das Flächenelement abstrahlt, so erhält man die
spektrale spezifische Ausstrahlung des Schwarzen Strahlers. Das Integral
liefert einen zusätzlichen Faktor .
Zur Formel siehe den Artikel „Plancksches
Strahlungsgesetz“.
Gesamtstrahldichte eines Schwarzen Strahlers
Integriert man die spektrale Strahldichte über alle Frequenzen bzw.
Wellenlängen, so erhält man die Gesamtstrahldichte :
Die Auswertung des Integrals liefert wegen :
mit
: Gesamtstrahldichte des Schwarzen Strahlers, W m−2 sr−1.
ist die Strahlungsleistung, die vom Flächenelement dA auf allen
Frequenzen in das in der Richtung β gelegene Raumwinkelelement dΩ abgestrahlt
wird.
Das Verhältnis der in eine bestimmte Richtung abgegebenen Gesamtstrahldichte eines Flächenelements eines gegebenen Strahlers zu der Gesamtstrahldichte eines Schwarzen Strahlers derselben Temperatur ist der gerichtete Gesamtemissionsgrad des Flächenelements.
Integriert man die Gesamtstrahldichte des Schwarzen Strahlers über alle
Richtungen des Halbraums, in den das Flächenelement abstrahlt, so erhält man die
spezifische
Ausstrahlung des Schwarzen Strahlers. Das Integral liefert einen
zusätzlichen Faktor .
Zur Formel siehe den Artikel „Stefan-Boltzmann-Gesetz“.
Anwendung
Umstellen der Definitionsgleichung für die Strahldichte liefert die
Strahlungsleistung, die vom Flächenelement
in das Raumwinkelelement
gestrahlt wird, welches in der durch die Winkel
und
beschriebenen Richtung liegt:
Soll die Ausstrahlung einer endlich großen Abstrahlfläche
in einen endlich großen Raumwinkel
ermittelt werden, so ist über
und
zu integrieren:
Dabei wurde die Darstellung des Raumwinkelelements in Kugelkoordinaten verwendet:
Da
im Allgemeinen vom Ort auf der Strahlfläche
und von den überstrichenen Richtungen abhängen kann, ergibt sich unter Umständen
ein sehr kompliziertes Integral. Eine wesentliche Vereinfachung tritt ein, wenn
die Strahlfläche ein lambertscher Strahler (die Strahldichte also
richtungsunabhängig) mit konstanten Oberflächeneigenschaften (die Strahldichte
also ortsunabhängig) ist. Dann ist die Strahldichte eine konstante Zahl
und kann vor das Integral gezogen werden:
Das Integral hängt jetzt nur noch von der Gestalt und Lage des Raumwinkels
ab und kann unabhängig von
gelöst werden. Auf diese Weise können nur von der Sender- und
Empfängergeometrie abhängige allgemeine Sichtfaktoren
ermittelt werden.
Wird beispielsweise die Ausstrahlung in den gesamten von der Strahlfläche
überblickten Halbraum betrachtet, so ergibt sich für das Integral der Wert
und die Abstrahlung eines lambertschen Strahlers der Fläche
in den gesamten Halbraum ist einfach:
(Strahlungsleistung eines lambertschen Strahlers in den Halbraum)
Ist die Strahlfläche ein Schwarzer Strahler
der Temperatur ,
so lässt sich die benötigte Strahldichte sofort nach dem planckschen
Strahlungsgesetz berechnen (Formeln siehe oben). Ist sie ein Grauer Strahler, so
ist die plancksche Strahldichte um den Emissionsgrad
abzumindern. Eine eventuelle Orts- und Richtungsabhängigkeit des Emissionsgrades
sowie eventuelle Reflexionen können die Integrationen erschweren.
Fotometrisches Grundgesetz
Ausstrahlung
_DE.png)
Betrachtet man ein Flächenelement ,
welches mit der Strahldichte
ein im Abstand
befindliches Flächenelement
bestrahlt, so spannt
von
aus betrachtet den Raumwinkel
auf, und aus der ersten Gleichung im vorigen Abschnitt folgt:
Dabei sind
und
die Neigungswinkel der Flächenelemente gegen die gemeinsame
Verbindungslinie.
Dies ist das fotometrische Grundgesetz. Durch Integration über die beiden Flächen ergibt sich wiederum die von Fläche 1 nach Fläche 2 fließende Strahlungsleistung.
Einstrahlung
Die Bestrahlungsdichte
(nicht zu verwechseln mit der Bestrahlungsstärke,
welche auch oft mit
bezeichnet wird) ist analog zur Strahldichte, jedoch für den Einstrahlungsfall
definiert. Sie gibt an, welche Strahlungsleistung
aus der durch den Polarwinkel
und den Azimutwinkel
gegebenen Richtung pro projiziertem Flächenelement
und pro Raumwinkelelement
empfangen wird. Die bisher abgeleiteten Gleichungen gelten analog. Insbesondere
gilt für die auf Flächenelement
empfangene, von
abgegebene Strahlungsleistung:
wobei diesmal der von
aufgespannte Raumwinkel
auftritt.
Folgerung
Die von
nach
ausgesandte und die auf
von
empfangene Strahlungsleistung müssen identisch sein (sofern nicht in einem
zwischen den Flächen liegenden Medium Strahlungsleistung durch Absorption oder
Streuung verloren geht), und aus dem Vergleich der beiden Gleichungen folgt:
Die von Fläche 1 ausgesandte Strahldichte ist identisch mit der auf Fläche 2 eintreffenden Bestrahlungsdichte.
Man beachte, dass die Strahldichte nicht mit dem Abstand abnimmt. Die gesamte
übertragene Strahlungsleistung
bzw.
nimmt hingegen wie erwartet mit dem Quadrat des Abstandes ab (aufgrund des
Faktors
im Nenner beider Gleichungen), dies liegt daran, dass der von der Senderfläche
aufgespannte Raumwinkel aus Sicht der Empfängerfläche quadratisch mit dem
Abstand abnimmt. Das photometrische
Äquivalent der Strahldichte ist die Leuchtdichte,
welche bekanntlich ebenfalls für flächig erscheinende Lichtquellen unabhängig
von deren Entfernung ist (eine nahe Plakatwand erscheint zwar größer aber nicht
heller als eine identisch beleuchtete weiter entfernte).
Wird die Bestrahlungsdichte über den Raumwinkel integriert, aus dem sie stammt, so ergibt sich die Bestrahlungsstärke genannte Einstrahl-Leistungsdichte auf der Empfängerfläche in W/m². Falls die Strahldichte der Senderfläche bekannt ist, so ist damit sofort auch die Bestrahlungsdichte der Empfängerfläche bekannt:
Beispiele
Die Sonne ist in guter Näherung ein Schwarzer Strahler der Temperatur 5777 K. Sie erscheint von der Erde aus gesehen unter einem Raumwinkel von 0,000068 Steradian. Man berechne die daraus folgende Bestrahlungsstärke an der Erdoberfläche (senkrecht zur Sonnenstrahlung und ohne Berücksichtigung der absorbierenden Atmosphäre).
Gemäß dem planckschen Strahlungsgesetz beträgt die Strahldichte der
Sonnenoberfläche .
Die Bestrahlungsdichte an der Erdoberfläche hat denselben Zahlenwert. Wird die
von der Sonne herrührende Bestrahlungsdichte als über die Sonnenscheibe konstant
angesehen, so reduziert sich die Integration über den von der Sonnenscheibe
eingenommenen Raumwinkel auf eine Multiplikation der Bestrahlungsdichte mit dem
Raumwinkel.
Es ergibt sich eine Bestrahlungsstärke von 20,10 × 106 W·m−2·sr−1 × 0,000068 sr = 1367 W·m−2, die Solarkonstante.
Ein grüner Laserpointer emittiert einen Lichtstrahl mit einer Leistung von einem Milliwatt. An der Austrittsöffnung hat der kreisförmige Strahl einen Radius von einem Millimeter. Der Radius vergrößert sich entlang der Strahlachse um 0,2 mm pro Meter. Berechne das Strahlparameterprodukt dieses Lasers, sowie den Raumwinkel den der Strahlkegel einnimmt und daraus die Strahldichte des Lasers.
Die gegebenen Zunahme des Radius entlang der Stahlachse um 0,2 mm pro Meter entspricht einem ebenen Winkel von 0,2 mrad. Das Strahlparameterprodukt dieses Lasers ergibt sich als Produkt aus diesem halben Öffnungswinkel und dem Radius des Strahls zu 0,2 mm·mrad.
Aus dem ebenen Winkel von 0,2 mrad berechnet sich der Raumwinkel in Steradiant zu 3,14 × 10−8 sr.
Um die Strahldichte zu bestimmen, wird noch aus dem gegebenen Radius die Fläche des Strahls an der Austrittsöffnung zu 3,14 mm² berechnet. Für die Strahldichte ergibt sich somit ein Wert von 1 mW / (3,14 mm² × 3,14 × 10−8 sr) = 10 GW·m−2·sr−1. Die Strahldichte des Lasers ist also um einen Faktor 500 größer als die der Sonne (20 MW·m−2·sr−1, siehe oben)!


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2022