Exponentieller Prozess

Bei einem exponentiellen Prozess handelt es sich um einen Vorgang, bei dem sich eine Größe exponentiell ändert. Man unterscheidet zwischen

exponentiellem Wachstum, bei dem eine Größe immer schneller wächst, und
exponentieller Annäherung, bei der sich eine Größe einem vorgegebenen festen Wert annähert. Der praktisch wichtigste Spezialfall hiervon ist der exponentielle Zerfall, bei dem eine Größe sich monoton abnehmend immer langsamer der Null nähert.

Meistens geht es dabei um zeitliche Änderungen.

Exponentielles Wachstum

Wenn bei einem Wachstumsprozess einer Größe die Wachstumsrate ${\tfrac {\mathrm {d} A}{\mathrm {d} t}}$ (also die positive zeitliche Änderung der Größe) proportional zur Größe selbst ist, liegt exponentielles Wachstum vor:

${\frac {{\mathrm {d}}A}{{\mathrm {d}}t}}\sim A$

Mit der Proportionalitätskonstanten $\tau$ erhält man aus dieser Proportionalitätsbeziehung die Differentialgleichung

$\tau \cdot {\frac {{\mathrm {d}}A}{{\mathrm {d}}t}}=A$

deren Lösung eine Exponentialfunktion ist:

$A(t)=A_{0}\cdot {\mathrm {e}}^{{{\frac {t}{\tau }}}}$

Damit bekommt $\tau$ die Bedeutung einer Zeitspanne, in der die Größe jeweils auf das e-fache anwächst. $A_{0}$ ist der Wert der Größe zu Beginn (bei Zeit t=0 ).

Exponentieller Zerfall

Exponentieller Zerfall einer zerfallenden Stoffmenge eines radioaktiven Nuklids mit Halbwertszeit

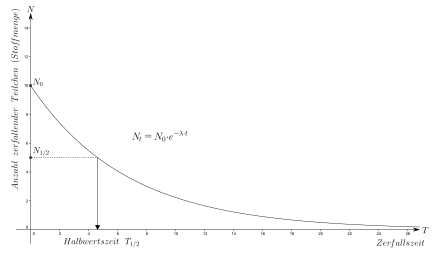
Ist die Abnahme einer Größe proportional zum jeweiligen Wert der Größe selbst, so spricht man von exponentiellem Zerfall, exponentieller Abnahme oder exponentiellem Abfall.

Beispiele

Zeitlich exponentielle Abnahme:

Radioaktiver Zerfall: In jeder Sekunde zerfällt ein feststehender Prozentsatz der vorhandenen Atomkerne der Substanz; je weniger Kerne noch vorliegen, desto langsamer nimmt ihre Zahl ab
Entladen eines Kondensators über einen Widerstand
Selbstinduktionsspannung bei Spannungsänderungen an einer Spule
Stromstärke beim Ausschaltvorgang einer Spule
Schwingungsamplitude eines gedämpften Pendels (bei Stokes-Reibung)
Entleeren eines Wasserbehälters durch einen dünnen Schlauch am Boden: Je tiefer der Wasserstand fällt, desto geringer wird der Wasserdruck im Schlauch und desto langsamer strömt das Wasser aus
Katalytischer Abbau von Stoffen durch eine chemische Reaktion, siehe Exponentialfunktion, Kinetik (Chemie).
Relaxation (NMR): Wiederaufbau der longitudinalen oder Zerfall der transversalen Kernmagnetisierung nach einer Störung.

Räumlich (mit der Eindringtiefe) exponentielle Abnahme:

Absorption mancher Strahlungen in homogenem Material

Mathematische Darstellung

Da die Abnahme eine negative Änderung ist, lautet die Differentialgleichung (hier für zeitliche Abnahme geschrieben) jetzt

$-\tau \cdot {\frac {{\mathrm {d}}A}{{\mathrm {d}}t}}=A$ (es ist üblich, ein positives $\tau$ anzunehmen und das Vorzeichen in die Gleichung zu schreiben)

und deren Lösung ist

$A(t)=A_{0}\cdot {\mathrm {e}}^{{-{\frac {t}{\tau }}}}$

$\tau$ ist also die Zeitspanne, in der die Größe jeweils auf das ${\tfrac {1}{{\mathrm {e}}}}$ -fache (etwa 37 %) abfällt. Man nennt $\tau$ Zeitkonstante, in der Physik auch Lebensdauer.

Eine anschaulichere Größe anstelle von $\tau$ ist die Halbwertszeit. Sie gibt an, innerhalb welcher Zeitspanne die Größe immer auf die Hälfte abnimmt, und lässt sich leicht aus der Zeitkonstante berechnen:

$T_{{\text{1/2}}}=\ln \,(2)\cdot \tau \approx 0{,}6931\cdot \tau$

Exponentielle Annäherung

Bei vielen physikalischen Prozessen gleicht sich eine physikalische Größe zwischen zwei miteinander verbundenen Körpern/Systemen aus.

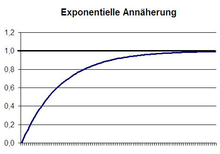
Exponentielle Annäherung an den Wert 1

Beispiele:

Die Temperatur eines Metallstücks gleicht sich an die Umgebungstemperatur an.
Die Temperaturen zweier unterschiedlich heißer, wärmeleitfähig verbundener Metallklötze gleichen sich einander an.
Die Spannung eines zu ladenden Kondensators nähert sich der Ladespannung an.
Die Stromstärke beim Einschaltvorgang einer Spule nähert sich der durch das ohmsche Gesetz gegebenen Stromstärke an.
Die Wasserstände zweier unterschiedlich gefüllter, mit einem dünnen Schlauch verbundener Wasserbehälter gleichen sich einander an.
Diffusion: Die Konzentrationen eines gelösten Stoffes in zwei miteinander verbundenen Kammern gleichen sich aus.
Die Fallgeschwindigkeit eines Körpers in einer Flüssigkeit endlicher Viskosität nähert sich ihrer Endgeschwindigkeit an (Stokes-Reibung).

Vielen dieser Beispiele ist gemeinsam, dass jeweils eine intensive Größe und eine extensive Größe miteinander in Beziehung stehen:

Temperatur und Wärmemenge (thermische Energie)
elektrische Spannung und elektrische Ladung am Kondensator
Wasserdruck und Volumen (oder Stoffmenge) in zylindrischen Behältern
Konzentration und Stoffmenge.

Die beiden Größen sind dabei jeweils proportional zueinander, und eine Differenz in der ersten Größe bewirkt, dass ein Fluss (oder Strom) der zweiten Größe zwischen den beiden Systemen fließt. Dieser wiederum bewirkt in den Systemen eine Änderung der ersten Größe:

Eine Temperaturdifferenz bewirkt einen Wärmefluss und damit Temperaturänderungen in beiden Körpern.
Eine Spannungsdifferenz am Kondensator bewirkt einen elektrischen Strom und damit eine Spannungsänderung.
Ein Konzentrationsgefälle bewirkt einen Stofftransport und damit Konzentrationsänderungen.
Eine Füllhöhendifferenz (und damit Druckdifferenz) bewirkt einen Materiefluss und damit Füllhöhenänderungen.

Die zeitliche Änderung der intensiven Größe ist dabei proportional zur Stärke des jeweiligen Flusses, und diese ist proportional zur Differenz der Größe. In einem solchen Fall gilt für eine Größe also die Differentialgleichung

$-\tau {\frac {{\mathrm {d}}A}{{\mathrm {d}}t}}=A_{2}-A_{1}$

Dieser grundlegende Sachverhalt ist für die oben beschriebenen Phänomene gleich, deshalb lassen sich Erkenntnisse und Gesetze zwischen diesen gut übertragen. Die Diffusionsgesetze beispielsweise gelten ebenso für die Wärmeleitung und elektrische Ladung. (Elektrische Phänomene sind allerdings meist sehr schnell. Bei Flüssigkeiten/Gasen ohne starke Reibung/Dämpfung sorgt die Trägheit der bewegten Masse für zusätzliche Effekte, meist in Form von Schwingungen und Schallwellen.)

Ist einer der beiden Werte konstant (Außentemperatur, Ladespannung), so wird sich die betrachtete Größe an diesen Wert annähern. Sind beide Werte variabel, so werden sie sich aneinander annähern. In beiden Fällen nähern sich die Werte einem Endwert $A_{{\text{Ende}}}$ an, den man meist leicht berechnen kann.

Als Differentialgleichung kann man schreiben

$-\tau {\frac {{\mathrm {d}}A}{{\mathrm {d}}t}}=A-A_{{\text{Ende}}}$

mit der Lösung

$A(t)=A_{{\text{Ende}}}+\left(A_{{\text{Anfang}}}-A_{{\text{Ende}}}\right){\mathrm {e}}^{{-{\frac {t}{\tau }}}}$

Dabei ist $A_{{\text{Anfang}}}$ der Wert von zu Beginn (bei Zeit t=0 ).

Der Exponentielle Abfall ist als Annäherung an den Wert 0 ein Spezialfall der Exponentiellen Annäherung mit $A_{{\text{Ende}}}=0$ .

Der Endwert A_Ende wird nie erreicht, sondern nur immer besser angenähert. In der Praxis wird die immer kleinere Differenz zum Endwert irgendwann kleiner als die Messungenauigkeit. Nach der fünffachen Zeitkonstante ( $t=5\tau$ ) ist die ursprüngliche Differenz bereits auf unter 1 % abgesunken, nach der siebenfachen ( $t=7\tau$ ) auf unter 1 ‰.

Die Zeitkonstante $\tau$ lässt sich im konkreten Fall bestimmen und hängt ab von Größen wie allgemeinen Widerständen und Kapazitäten. Beispielsweise ist beim Auf- oder Entladen eines Kondensators mit der Kapazität über einen Widerstand mit dem Wert :

$\tau =R\cdot C$ .

Siehe auch

Lebensdauer (Physik)

Basierend auf einem Artikel in:

Wikipedia.de