Anharmonischer Oszillator
Der anharmonische Oszillator ist ein schwingungsfähiges physikalisches System, bei dem die Rückstellkraft nicht proportional zur Auslenkung aus der Ruhelage ist. Das hat zur Folge, dass die Schwingung nicht streng sinusförmig verläuft. Mechanische Beispiele sind etwa Pendel (Anharmonizität bemerkbar bei größerer Auslenkung), Kippschwingungen (das Kippeln eines aufrecht stehenden Gegenstands), Hüpfen eines Balls auf einer ebenen Fläche.
Bei genauer Betrachtung sind fast alle realen schwingungsfähigen Systeme anharmonisch. Die meisten nähern sich aber einem harmonischen Oszillator an, je kleiner die Auslenkungen aus der Ruhelage sind, weil dann die Näherung einer linearen Rückstellkraft immer besser zutrifft (für die Mechanik siehe Hookesches Gesetz, Mathematisches Pendel). Bei solchen anharmonischen Oszillatoren verlaufen kleine Schwingungen näherungsweise sinusförmig und mit einer bestimmten Eigenfrequenz, der Grundfrequenz des Oszillators.
Beim anharmonischen Oszillator treten im Vergleich zum harmonischen Oszillator grundsätzlich neue Phänomene auf:
- Die Abweichung von der Sinusform bedeutet, dass die Schwingung auch Oberschwingungen (akustisch: Obertöne) der Grundfrequenz enthält.
- Bei unsymmetrischem Kraftgesetz verschiebt sich der Mittelpunkt der Schwingung gegenüber der Ruhelage. Dies tritt z.B. bei den Schwingungen zwischen den Atomen der festen Körper auf und ist die Ursache von deren thermischer Ausdehnung.
- Bei äußerer Anregung mit einer periodischen Kraft hat die entstehende erzwungene Schwingung Anteile mit der Differenzfrequenz von Anregungsfrequenz und Grundfrequenz und anderen ganzzahligen Kombinationen davon. Technische Anwendung findet dies z.B. in der nichtlinearen Optik bei der Frequenzverdopplung bei Laserlicht.
- Bei äußerer Anregung mit einer periodischen Kraft kann der anharmonische Oszillator auch mit einer chaotischen Bewegung reagieren, wenn die Anfangsbedingungen entsprechend gewählt sind oder seine Parameter außerhalb bestimmter Grenzen liegen (z.B. bei zu geringer Dämpfung).
Bewegungsgleichung
Es gibt eine Vielzahl unterschiedlicher anharmonischer Oszillatoren und
entsprechend viele Bewegungsgleichungen. Ihnen gemeinsam ist, dass ihre
Rückstellkraft nicht wie beim harmonischen Oszillator gemäß
nur linear von der Auslenkung
abhängt, sondern auch von höheren Potenzen von
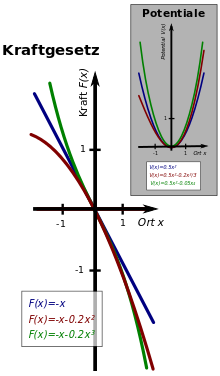
("nichtlineares Kraftgesetz"). In der nebenstehenden Abbildung sind die
einfachsten Beispiele zusammen mit dem genäherten linearen Kraftgesetz (blaue
Gerade) dargestellt:
- A) Ein einfaches asymmetrisches Kraftgesetz (rote Kurve im
Bild rechts) lautet
.
- Eine Umformung
lässt erkennen, dass der nichtlineare Term die Rückstellkraft zur einen Seite hin zunehmend schwächt und zur anderen Seite hin stärkt, sofern die Auslenkungen nicht zu groß werden (
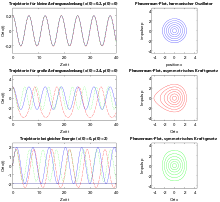
). Wie man an den Trajektorien
in der zweiten Abbildung sieht, führt dies zu einer im Vergleich zum harmonischen Oszillator stärkeren Auslenkung des Oszillators in die Richtung der abgeschwächten Rückstellkraft und zu einer verlangsamten Periode. Ein solches asymmetrisches Kraftgesetz kann etwa als zweite Näherung (nach dem linearen Kraftgesetz) an das unten erwähnte Morse-Potential in der Molekülphysik genutzt werden.
- Eine Umformung
- B) Ein einfaches symmetrisches Kraftgesetz (grüne Kurve im
Bild rechts) lautet
.
- Je nach Vorzeichen von
wächst die Rückstellkraft, im Vergleich zum harmonischen Oszillator, zunehmend stärker (
) oder schwächer (
) an. Im ersten Fall erfolgen die Schwingungen bei gleicher Amplitude schneller, im zweiten Fall langsamer.
- Zum Beispiel ist dies Kraftgesetz für
eine Näherung für das Schwere- oder mathematische Pendel, dessen Schwingungsperiode mit zunehmender Amplitude zunimmt. Die Größe
steht in diesem Fall für den dimensionslosen Auslenkungswinkel des Pendels. Eine solche Näherung ergibt sich, wenn man die Rückstellkraft
des mathematischen Pendels in einer Taylorreihe bis zur dritten Ordnung in
entwickelt:
- Je nach Vorzeichen von
Die Bewegungsgleichungen
mit dem Dämpfungsterm
ergeben sich dann aus dem Newton'schen
Gesetz
wobei
die erste und
die zweite Ableitung der Funktion
nach der Zeit
bezeichnet, zu:
-
- Fall A:
- Fall B:
- Fall A:
Für
erhält man wieder in beiden Fällen das lineare Kraftgesetz sowie die
Differentialgleichung des gedämpften harmonischen Oszillators. Auch für kleine
Auslenkungen ist die Lösung des anharmonischen Oszillators wieder nahezu
harmonisch, wie die ersten Trajektorien in der Abbildung rechts zeigen.
Durch die Nichtlinearität der Differentialgleichungen wird das Superpositionsprinzip
außer Kraft gesetzt. Das bedeutet, dass nicht mehr jedes Vielfache
einer Lösung
,
auch eine Lösung der Differentialgleichung ist und allgemeiner, dass mit zwei
Lösungen
nicht jede Linearkombination
auch eine Lösung ist (wobei
beliebige feste Zahlen sind). Die Lösung der Bewegungsgleichung ist meist ein elliptisches
Integral und daher in geschlossener Form mit elementaren Funktionen nicht
darstellbar. Dieser Artikel konzentriert sich auf periodische Bewegungen des
anharmonischen Oszillators. Dabei wird die Dämpfung stellenweise vernachlässigt,
d.h.
gesetzt. Nur so ergeben sich, falls keine äußere Kraft einwirkt, periodische
Bewegungen im strengen Sinne.
Näherungslösung
Im Fall einer schwachen anharmonischen Störung, d.h.
bzw.
,
kann man die Lösung durch Störungsrechnung
erhalten. Dazu gibt man
in Form einer Potenzreihe eines Störparameters
an:
Dabei ist das erste Glied die (den Anfangsbedingungen angepasste) Lösung für
den harmonischen Fall ,
z.B.
,
wenn der Oszillator zur Zeit
bei der Auslenkung
mit Geschwindigkeit
freigegeben wird und die Grundfrequenz
hat.
Nach Einsetzen von
in die Bewegungsgleichung, wobei
durch
ausgedrückt wird, ergibt sich eine Potenzreihe in
,
deren Koeffizienten sämtlich gleich Null zu setzen sind. So erhält man
Differentialgleichungen für die einzelnen Näherungsfunktionen
,
die rekursiv zu lösen sind. Konkret hat die Differentialgleichung für
die Form der Bewegungsgleichung für einen harmonischen Oszillator, der von einer
externen Kraft, welche durch die vorherigen
gegeben ist, zu erzwungenen Schwingungen angeregt wird.
Im Fall A folgt im ersten Schritt
Hier tritt bereits die verdoppelte Grundfrequenz auf. Der mathematische Grund
dafür lässt sich zurückverfolgen zum Auftreten des quadratischen Terms
in der Bewegungsgleichung, der durch die trigonometrische Identität
linearisiert wird. Bei den weiteren Näherungen ergeben sich Summanden mit
entsprechend höheren Vielfachen der Grundfrequenz, insgesamt also ein ganzes
Spektrum von Oberschwingungen.
Im Fall B ergibt sich im ersten Schritt eine instabile Lösung, denn
enthält einen zu
proportionalen Term. Dieser lässt sich jedoch eliminieren, wenn
gesetzt wird. So ergibt sich schon in 1. Näherung eine Abhängigkeit der
Oszillationsfrequenz
von der Amplitude
(wie im Fall A erst im 2. Schritt).
Anwendungen
Real in technischen Geräten verbaute Federn weisen im Allgemeinen, zuweilen auch durch die Konstruktion beabsichtigt, nur in gewissen Grenzen eine lineare Beziehung zwischen Rückstellkraft und Auslenkung auf. Die Dynamik eines Systems mit solchen Federn folgt dann den nichtlinearen Bewegungsgleichungen, wie sie oben eingeführt wurden.
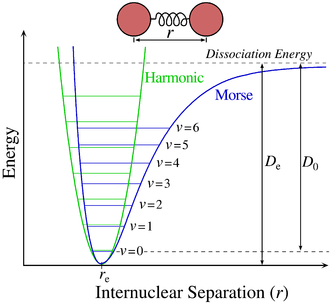
Wichtige Anwendungen für anharmonische Schwingungen finden sich etwa in der Molekülphysik bei der Schwingung zweiatomiger Moleküle, oder in der Festkörperphysik bei wärmebedingten Schwingungen von Atomen. Die Anharmonizität bildet sich durch die unterschiedlichen Effekte bei Annäherung (elektrostatische Abstoßung, teilweise durch die Elektronen der Atomhülle abgeschirmt, aber durch das Pauli-Prinzip verstärkt) und Entfernung (Rückstellkraft durch die kovalente Bindung der Atome) der Atomrümpfe aus. Wie in der Abbildung rechts gezeigt, können solche Schwingungen etwa in einem Morse-Potential berechnet werden.
Erzwungene anharmonische Schwingungen
Bei der Bewegung unter dem Einfluss einer zeitabhängigen äußeren Kraft
unterscheiden sich anharmonischer und harmonischer Oszillator grundsätzlich
voneinander. Beispielsweise kann, auch nach Beendigung eines Einschwingvorgangs,
der anharmonische Oszillator mit anderen Frequenzen schwingen als in der
erregenden Kraft vertreten. Es kann auch bei langsamer Variation der
Erregerfrequenz zu sprunghafter Änderung der Amplitude kommen. Diese Phänomene
sind auch praktisch von großem Interesse, da reale Oszillatoren sich nur solange
harmonisch verhalten, wie bestimmte Grenzen für Auslenkung und/oder Frequenz
eingehalten werden.
Diese Phänomene lassen sich ganz allgemein auf die nicht-lineare Form der Bewegungsgleichung zurückführen, womit das Superpositionsprinzip hier nicht mehr angewendet werden kann. Einige der Konsequenzen:
- Es gibt kein allgemein gültiges Lösungsverfahren wie bei den erzwungenen Schwingungen des harmonischen Oszillators. Man muss die Bewegungsgleichung numerisch integrieren oder analytische Lösungen verwenden, die nur unter Näherungsannahmen zu gewinnen sind.
- Der Einschwingvorgang (bei periodischer Anregung) ist nicht durch die Überlagerung der stationären Schwingung mit einer freien Schwingung gegeben.
- Die eingeschwungene stationäre Schwingung ist nicht immer unabhängig von den Anfangsbedingungen.
- Nach Fouriertransformation bleiben die Bewegungsgleichungen für verschiedene Frequenzen miteinander gekoppelt.
Amplitudensprünge
Als Beispiel sei das symmetrische Kraftgesetz (der obige Fall B)
untersucht: Die Bewegungsgleichung lautet (nach Division durch ,
mit
sowie
):
Ausgehend von der Annahme einer stationären harmonischen Schwingung
ergibt sich daraus für die verursachende Kraft
- (**)
.
Der mit
oszillierende Anteil der Kraft rührt von der Umformung
her. Dieser Anteil wird im Weiteren vernachlässigt. Die Kraft lässt sich dann
näherungsweise zu
zusammenfassen, so dass hier eine mit der Frequenz
harmonisch schwingende Kraft eine harmonische Schwingung derselben Frequenz
erzeugt. Dabei ist
eine Phasenverschiebung und die Amplitude der Kraft durch
gegeben. Diese Gleichung lässt sich zwar nicht in der für die Resonanzkurve
üblichen Form
umstellen. Jedoch kann man sie nach
auflösen und erhält den Zusammenhang zwischen Erregerfrequenz
und stationärer Schwingungsamplitude
(für die durch
gegebene Kraftamplitude) in der Form:
.
Die beiden Lösungen ,
die hier durch die Lösung einer quadratischen Gleichung entstehen, drücken aus,
dass im Allgemeinen zwei Erregerfrequenzen zu gleich großer Amplitude der
stationären Schwingung führen, wie es auch schon beim harmonischen Oszillator
links und rechts der Resonanzspitze der Fall ist. Für den harmonischen Fall,
,
stimmt diese Formel mit der Resonanzkurve der harmonischen erzwungenen
Schwingungen überein, die ihr Amplitudenmaximum bei
hat und zu beiden Seiten hin symmetrisch abfällt. Neu ist beim anharmonischen
Oszillator, dass die Resonanzfrequenz sich mit steigender Amplitude verschiebt
(Term
in der Formel). Dadurch kann sich im Schaubild der Resonanzkurve
die ganze Resonanzspitze derartig krümmen, dass sie in bestimmten
Frequenzbereichen eine S-förmige Gestalt annimmt, also trotz gleicher
Kraftamplitude
und Erregerfrequenz
bis zu drei verschiedene mögliche Werte für die stationäre Amplitude
anzeigt. Wird bei langsamer, stetiger Variation der Erregerfrequenz solch ein
Bereich erreicht, springt die Amplitude von einem Ast der Resonanzkurve auf
einen anderen: Die Schwingung "kippt".
Subharmonische Anregung
Im vorigen Abschnitt wurde ein Beitrag zur Kraft, der mit der Frequenz
oszilliert, in der Gleichung (**) einfach weggelassen. Das ist nicht immer
gerechtfertigt, denn dieser Beitrag kann bei bestimmten Bedingungen auch die
Hauptrolle spielen. Wenn gilt, dass
sowie
,
dann verschwinden aus Gleichung (**) alle mit
periodischen Terme. Es bleibt:
ist eine Lösung zur externen Kraft
.
Beispiel: Das mathematische Pendel mit Grundfrequenz
(
Erdbeschleunigung,
Pendellänge), das Kraftgesetz genähert durch Wahl des Parameters
,
werde angetrieben durch eine externe Kraft
.
Dann schwingt es mit Amplitude
und einer dreifach untersetzten Frequenz wie
.
Um dies Verhalten beobachten zu können, muss man allerdings entweder die
richtigen Anfangsbedingungen treffen oder das Abklingen von zusätzlichen
Eigenschwingungen abwarten, was wegen der Annahme einer vernachlässigbar
geringen Dämpfung sehr lange dauern kann.
Intermodulation
Mit Intermodulation wird das Phänomen bezeichnet, dass der Oszillator bei
Anregung mit zwei Frequenzen
mit einer Schwingung antwortet, in der auch Kombinationsfrequenzen
(
und
ganzzahlig) vertreten sind. Während des Einschwingvorgangs, der aber wegen der
Dämpfung gewöhnlich nur kurz dauert, sind solche Frequenzvielfache und
Kombinationsfrequenzen auch in Bezug auf die Grundfrequenz
vorhanden. In der Akustik können sie als hörbare Töne auftreten, die ihre
Ursache also darin haben, dass das Trommelfell oder eine Lautsprechermembran
über diejenige Auslenkung hinaus erregt wird, bis zu der ein lineares
Kraftgesetz für die Rückstellkraft gilt.
Literatur
Friedhelm Kuypers: Klassische Mechanik. 8. Auflage. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40721-7.
Siehe auch
- Van-der-Pol-System
- Harmonischer Oszillator
- Harmonischer Oszillator (Quantenmechanik)
- Störungstheorie (Quantenmechanik)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.08. 2025