Jones-Formalismus
Der Jones-Formalismus beschreibt lineare optische Abbildungen unter Berücksichtigung der Polarisation. Das Licht wird als ebene elektromagnetische Welle repräsentiert, mit einem komplexwertigen zweidimensionalen Jones-Vektor, der Amplitude der Welle. Damit ist die Anwendung auf vollständig polarisiertes, kohärentes Licht begrenzt. Die Abbildungen werden durch Jones-Matrizen dargestellt. Der Formalismus wurde nach R. Clark Jones benannt, der diese Darstellung 1941 einführte. Der Jones-Formalismus eignet sich insbesondere zur Analyse optischer Systeme, in denen ein Lichtstrahl eine Kaskade von optischen Bauelementen durchläuft.
Mathematische Beschreibung
| Polarisation | Polarisationsrichtung zu
verschiedenen Zeiten bei z=0 |
Jones-Vektor | Bra-Ket-Notation |
|---|---|---|---|
| linear in x-Richtung | |||
| linear in y-Richtung | 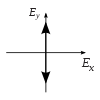 |
||
| linear in +45°-Richtung | 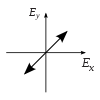 |
||
| links zirkular | 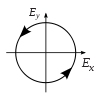 |
||
| rechts zirkular | 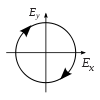 |
In komplexer Schreibweise hat die Elongation einer monochromatischen ebenen Welle in einem kartesischen Koordinatensystem die Orts- und Zeitabhängigkeit
,
wobei als Ausbreitungsrichtung die -Achse
gewählt ist. Die reellen Zahlen
und
bezeichnen die Kreiswellenzahl
bzw. die Kreisfrequenz
der Welle. Die komplexen Zahlen
bzw.
beschreiben Phase und Amplitude der
bzw.
Komponente des Feldes. Der Jones-Vektor dieser Welle ist dann
,
das heißt, die explizite Raum- und Zeitabhängigkeit der Amplitude wird bei der Beschreibung der Welle unterdrückt. Des Weiteren wird in der Darstellung eines Jones-Vektors werden üblicherweise dessen Komponenten der auf 1 normalisiert und ein Vorfaktor eingeführt, damit die Intensität unverändert bleibt (siehe Beispiele).
Der Effekt eines optischen Bauelements auf die Lichtwelle lässt sich durch
die Wirkung einer komplexwertigen 2×2-Matrix
auf den Jones-Vektor beschreiben, wenn das Element keine nichtlinearen
Eigenschaften hat,
Durchläuft der Lichtstrahl ein System optischer Elemente mit Jones-Matrizen
,
so lässt sich der Gesamteffekt des optischen Systems durch eine Jones-Matrix
beschreiben (sofern Mehrfachreflexionen zwischen den einzelnen Komponenten keine Rolle spielen). Die Eigenpolarisationen eines optischen Systems entsprechen den Eigenvektoren seiner Jones-Matrix. Der Jones-Vektor eignet sich nur für die Beschreibung vollständig polarisierten Lichts, und entsprechend können nur optische Komponenten, die keine depolarisierenden Eigenschaften besitzen, durch Jones-Matrizen charakterisiert werden. Sind Depolarisations-Effekte von Bedeutung, muss auf den aufwändigeren Stokes-Formalismus zurückgegriffen werden.
Jones-Matrizen können z.B. lineare Polarisationen oder zirkulare
Polarisationen (Rotation der Polarisationsebene) und Verzögerungsplatten
beschreiben. Bei der -Viertel
Platte wird z.B. eine Polarisationsrichtung gegenüber der dazu senkrechten
um eine Viertel Wellenlänge verzögert. Bei zirkularer Polarisation und
Verzögerung ändert sich der Betrag der Gesamtamplitude nicht, und die Matrizen
sind unitär,
es gilt
(dabei bedeutet
komplex konjugiert und T die Transposition
der Matrix) und
.
Bei linearer Polarisation kann sich der Betrag der Gesamtamplitude ändern, die
zugehörigen Matrizen sind nicht unitär.
| Optisches Element | Jones-Matrix |
|---|---|
| Polarisationsfilter
für linear polarisiertes Licht
in H-Stellung |
|
| Polarisationsfilter für linear polarisiertes Licht,
in V-Stellung |
|
| Polarisationsfilter für linear polarisiertes Licht,
in +45°-Stellung |
|
| Polarisationsfilter für linear polarisiertes Licht,
in −45°-Stellung |
|
| Polarisationsfilter für linear polarisiertes Licht, um den Winkel
|
|
| Polarisator für links zirkular polarisiertes Licht | |
| Polarisator für rechts zirkular polarisiertes Licht | |
| λ/2-Plättchen mit schneller Achse in x-Richtung | |
| λ/4-Plättchen mit schneller Achse in x-Richtung |
Gemäß der üblichen Sprechweise in der Optik, bezeichnen „H“ wie horizontal und „V“ wie vertikal die Orientierung in die x- und y-Richtung. Wenn es nicht auf die Interferenz mit anderen Strahlen ankommt, kann ein gemeinsamer (komplexer) Phasen-Vorfaktor ausgeklammert werden, und die Matrizen werden häufig so angegeben, dass die erste Diagonalstelle reell ist.
Gedrehte Bauteile
Wird ein optisches Bauteil gegenüber seiner optischen Achse um den Winkel θ gedreht, so ist die Jones-Matrix für das gedrehte Bauteil M(θ). Diese Matrix erhält man aus der Matrix M für das ungedrehte Bauteil durch folgende Transformation:
- Dabei ist
Übergang zur Quantenmechanik
Man kann die reine x- und reine y-Polarisation als Orthonormalbasis
auffassen und diese in Bra-Ket-Schreibweise
darstellen, wie oben in der Tabelle angedeutet. Ein Polarisationsfilter lässt
sich dann zum Beispiel als quantenmechanischer
Operator auffassen, der auf einen Eigenzustand
des Systems (reine x- oder y-Polarisation) projiziert (Kollaps der
Wellenfunktion). Der entsprechende Projektor wäre
für einen x-Polarisationsfilter:
Der Eigenwert
entspricht dann dem Anteil des einfallenden Lichtes, das die entsprechende
Polarisation aufweist. Die Observable
ist die Polarisation in x-Richtung. Analog lassen sich die oben angegeben Filter
für zirkular polarisiertes Licht konstruieren.
In der Bra-Ket-Darstellung lässt sich auch ein Basiswechsel leicht
ausführen. Die Basiswechselmatrix ,
die von der x/y-Basis in die Darstellung durch Superposition von
gegensinnig zirkular polarisierten Wellen überführt hat folgende Gestalt.
Solche Überlegungen bieten einen anschaulichen Bezug zu den sonst eher abstrakten Formalismen der Quantenmechanik.
Siehe auch


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 13.06. 2022